3 3 Алгоритм проведения косвенного измерения

Косвенные измерения – это такие измерения, когда искомое значение физической величины получают на основании известной функциональной зависимости между данной величиной и др. величинами, значение которых определяют путем прямых измерений.

Алгоритм проведения косвенных измерений:

1. Обработать результаты измерений величин X и Y отдельно по алгоритму, изложенному далее:

• определить оценки результатов измерений X, У и средних квадратических отклонений S_x, S_y;

• обнаружить и исключить ошибки;

• проверить гипотезу о нормальности распределения оставшихся результатов измерений.

2. Определить оценку среднего значения функции:

3. Определить поправку

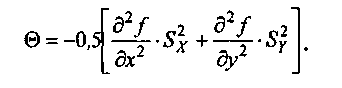
3. Определить оценку стандартного отклонения функции:

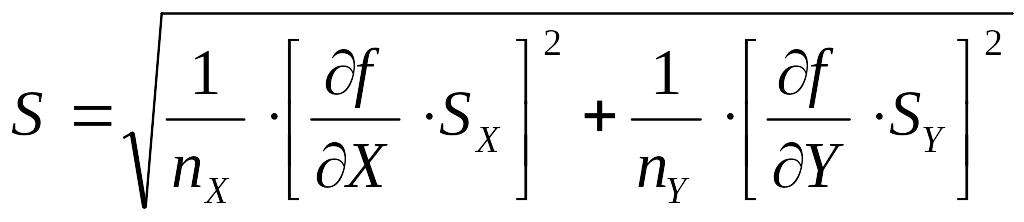
5. Определить доверительный интервал для функции:

Если законы распределения вероятности результатов измерения X и Y признаны нормальными, то t можно определить для принятой вероятности Р=0,95 из таблиц распределения Стьюдента. При этом число степеней свободы m определяется из выражения

;

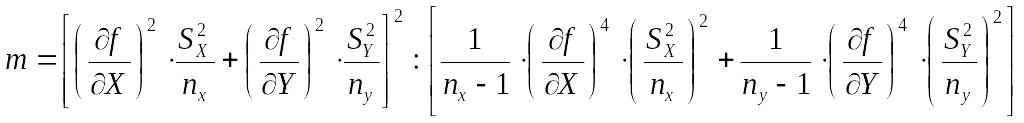Если гипотеза о нормальности распределения результатов изме­рения X или (и) Y отвергается, то t целесообразно определить из нера­венства Чебышева: Р > 1 - 1/t².

Результат записывается в виде:

Z= , с вероятностью P=…., n_x=…, n_y=….

35 Основные составляющие погрешностей измерительных цепей: погрешности приближения.....

Точность СИ оценивается величиной погрешности, под которой понимается разность между его индивидуальной и заданной характеристиками (междуд показаниями прибора и значени­ем измеряемой величины): ∆у(х) = у_и(х) – у₀(х). Погрешность измерит. устр-ва возникает - не удается обеспечить равенство заданной и индивид. хар-к.

Погрешность приближения (погрешность схемы) возникает на этапе структурного синтеза, когда с целью упрощения вместо заданной характеристики реализуется приближенная к ней характеристика. Введение погрешности приближения приводит к упрощению конструкции и технологии изготовления измерительного устройства: повышается точность изготовления и сборки деталей и элементов, а суммарная погрешность оказывается меньше, в связи с упрощением схемы повышается надежность и снижается себестоимость проектируемого уст­ройства. Погрешность приближения - это систематическая погрешность. Примерами приборов с погрешностью приближения нелинейные рычажно-зубчатые индикаторы с равномерной шкалой, электрические приборы для измерения неэлектрических величин, построенные на базе неуравновешенного моста с нелинейной характеристикой, цифровые приборы (дискретизация или квантование сигнала приводят к несоответствию заданной и расчетной характеристик). Определения погрешности приближения:

аналитический метод – погрешность находят как разность м/д номинальной расчетной и заданной хар-ки.

алгоритм: 1) выделяются элементарные преобраз-ные звенья и устанавл-ся связи м/д ними, составляется функц. схема; 2) на основании априорной инф-ции и справочных данных составляются ф-ции преобраз-я элементарных звеньев и записываются ур-я связей; 3) решается с-ма ур-ний, включающая хар-ки элементарных преобраз-х звеньев и ур-я связей, составляется искомая расчетная хар-ка.

экспериментальный метод при испытании опытных образцов: берут N экземпляров одно­типных объектов, каждый из к-х п раз поверяют в т точках в пределах всего диапазона. Алгоритм: 1) каждое измерит. устр-во многократно поверяют в выбранных точках и находят средние значения погрешностей в каждой точке; 2) по средним значениям погрешностей определяют в тех же точках средние значения погрешно­стей для всей группы объектов; 3) экспериментально полученные значения математ. обрабатывают для получения аналитической зависимости ф-ции погрешности схемы на основании ее экспериментального значения.

Погрешности от несоответствия размеров и параметров номинальным – производственно-технологические погрешности, обусловленные проблемами изготовления объекта, реальная характеристик каждого устройства сугубо индивидуальна и всегда отличается от номинальной расчетной. Технологические погрешности носят случайный характер. Источниками технологических погрешностей являются: – несоответствие первичных компонентов и неидентичность техпроцессов при изготовлении материалов для деталей; – несовершенство техпроцессов и оборудования, применяемых при изготовлении деталей и элементов; – несовершенство сборочных, регулировочных и контрольных приспособлений и операций.

Процесс изм-я парам-ра q_n хар-ся з-ном распр-я вероят-ти погр-ти f(Δ q_n), который оцен-ся мат ожиданием и СКО (М(Δ q_n) и S(Δ q_n)). При этом в констр-й док-ции задано поле допуска, характер-е нижним EI(Δ q_n) и верхним ES(Δ q_n) предел-ми отклонениями. На основании инф-ции о поле допуска и др. априорной информации найти мат ожидание и СКО погр-ти для того, чтобы применить рассматриваемый матем-й аппарат для анализа влияющих факторов.К рассмотрению принимаются след-е хар-ки: 1) Середина поля допуска отн-но ном-го значения пар-ра: Е₀=(EI+ES)/2.

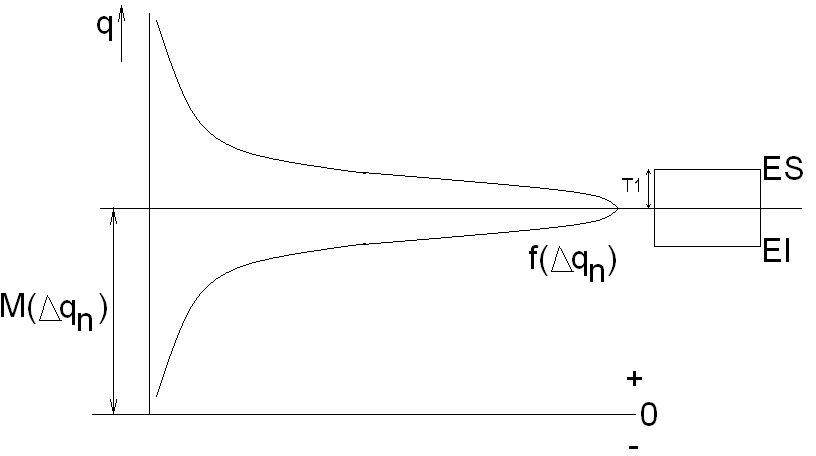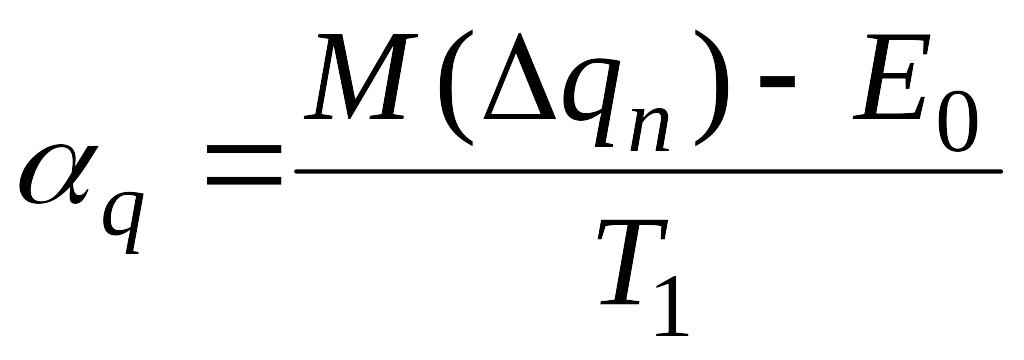2 )Половина поля допуска Т₁=(ES-EI)/2 3)Коэффициент относит-й асимметрии, который оценивает величину удаления центра группирования от середины поля допуска: . 4) Коэффициент рассеяния (Относит-е СКО), хар-щий. Какую долю составляет СКО от величины половины поля допуска:

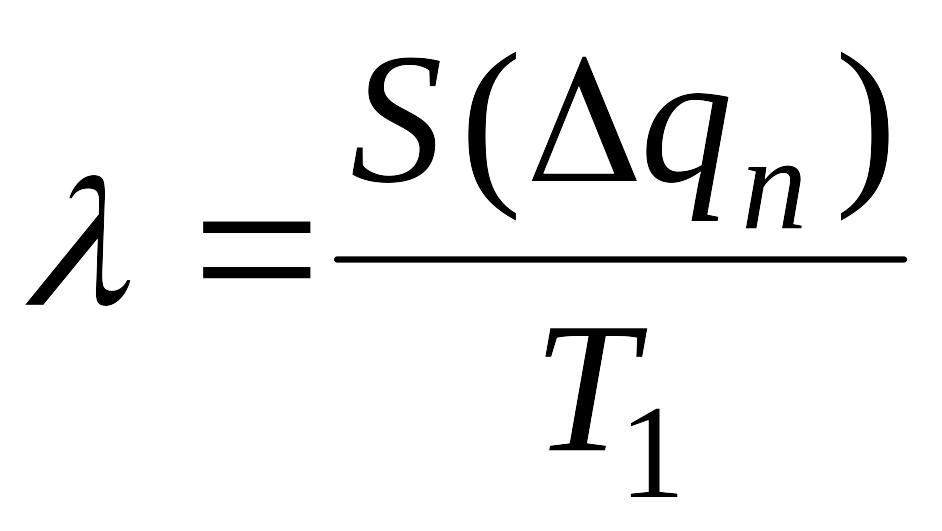
M(Δq_n)=E₀ _q=0; ;

Значения Е₀ и Т₁ определ-ся из докум-ции, а для нах-я точечных оченок необх-мо знать коэф-т отн-й асимметрии _q и коэф-т рассеяния , к-рый опр-ся из распр-я самих технологич-х погр-й. Существуют 3 подхода к опр-ю этих хар-к: 1) Определение кривых распр-я по производственнымным наблюдениям путём экспирим-го иссл-я. Применяется в том случае, если рассчитываемый объект уже изг-ся, тогда опр-ся гистограмма по к-рой опр-ся М(Δ q_n) и S(Δ q_n) по к-рым опр-ся _q и . 2) Изучение техпроцесса окончат-й обработки. Типовые техпроцессы хар-ся опр-ми видами з-на распр-я погр-й, которые приводятся в соотв-й справочной лит-ре. 3) Выбор кривых распр-я из схематизир-х таблиц. Где указано для разл-х типовых процессов з-ны распр-я и значения _q и . В этом случае частная погр-ть нах-ся из след-х завис-й:

;

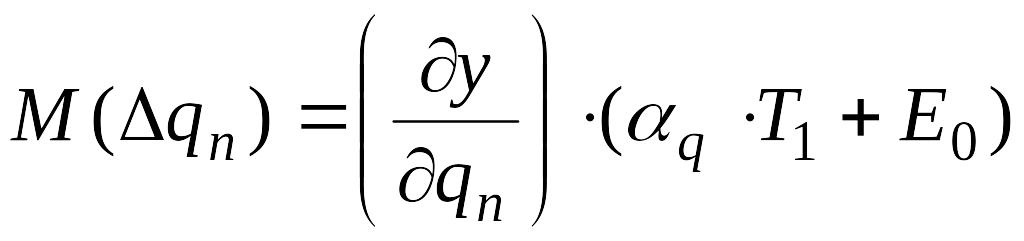К числу погрешностей от несоответствия параметров номинальным значениям относятся также погрешности из-за износа деталей и старения материалов, а также погрешности от внешних возмущающих воздействий (помех).

Влияющими факторами в последнем случае являются:

– климатические (температура, влажность, давление);

– механические (наклоны, переносные линейные и угловые ускорения, удары, вибрация);

– параметры режимов питания (напряжения, частота, давление, расход);

– параметры внешних полей (магнитных, электрических, радиационных, гравитационных) и т.п. воздействия.

Исключить влияние внешних воздействий невозможно, поэтому погрешность данного типа всегда имеет место. Она является случайной, хотя может иметь существенную систематическую составляющую, например температурная погрешность.

Каждую отдельную неточность внутр. параметра, приводящую к погрешности измерит. цепи, наз. первичной погрешностью (имеет размерность внутр. параметра) у = f(x, q₁, q₂,…q_n); q₁→∆q₁; q₂→∆q₂; q_n→∆q_n – это первичные погрешности. Часть суммарной погрешности проектир. устр-ва, обусловленная первичной погрешностью, называется частной или частичной (имеет размерность выходного сигнала). q₁→∆у_q1; q₂→∆у_q2; q_n→∆у_qn. ∆у_q1→∆y_Σ; ∆у_q2→∆y_Σ; ∆у_qn →∆y_Σ– это суммарные погрешности. Алгоритм опред-я первич. погрешностей:1)Составление перечня первичн. погрешностей,2) Составление описания первичн. погрешностей с учетом их вида (скаляр и вектор, детерминирован и случайн).

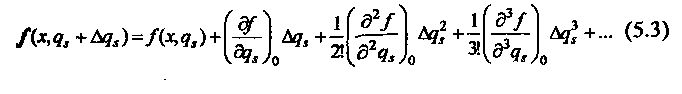
Методы определ-я частных погрешностей.

1 Аналитич. метод для детерминир. скалярных первич. погрешностей. Номин. расчетн. хар-ка: у_нр=f(x, q_n). q_n – совок-ть внутр. параметров устр-ва и имеет первичную погрешность ∆q_n. В р-те ф-ция преобраз-я: у_р=f(x;q_n+ ∆q_n).Разница между 2мя ф-циями составит частн. погрешность от влияния совокупности внутр. параметров: ∆у_∆qn= у_р- у_нр. Пусть ∆q_n<<q_n, поэтому выражение для расчетной ф-ции можно разложить в ряд Тейлора по степени ∆q_n.

Символ ( )₀ означает, что при взятии частных производных значения всех параметров принимаются без учета первичных погрешностей. Пренебрегая величинами 2го и больших порядков малости, выражение для расчетной ф-ции преобраз-я:

С учетом этого выражение для частной погрешности можно записать в следующем виде:

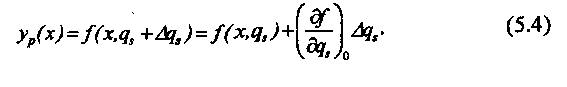
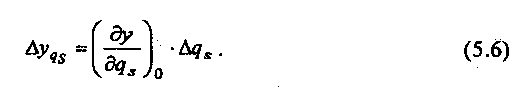
Это выражение наз. осн. формулой линейной теории точности, а значение dy/dq_n наз. Коэф-м влияния. Т.о. для нахождения частной погрешности необходимо детерминир. скалярную первичную погрешность умножить на коэф-т влияния. Аналитич. метод опред-я частных погрешностей явл-ся наиболее эффектным, удобным и рекомендуется к применению. Использование не всегда возможно. Ограничение 1: первич погрешность д/б много меньше номинальн. знамения параметра. Ограничение 2: метод не м/б применен в случае нулевых номинальн. значений параметра, поскольку тогда значение параметра отсутствует в расчетной хар-ке, и частную производную взять нельзя. Ограничение 3: при сложных ф-циях преобраз-я м/б затруднительным взятие частных производных. Ограничение 4: метод м/б использован в рассмотренном виде только для независимых первич. погрешностей.

2 Метод преобразованных схем. первич. погрешность моделируют с помощью дополнит. генераторов в электрич. цепи. При этом искомое значение частной погрешности определяют как ф-цию вых. сигнала при неизменном вх. сигнале и при применении моделирования к первичной погрешности.

3 Геометрический метод применяется при расчете точности механизмов, при этом механизм строят в 2х положениях, наложенных одно на другое. Одно из них без погрешности, другое – с погрешностью. Искомое значение погрешности определяют из геометрических соотношений, используя для этого правила и законы геометрии.

Погрешности от действия внутренних дестабилизирующих факторов (материально-структурные погрешности) возникают под влиянием дополнит. (вредных) возд-й, не предусмотренных принципом действия прибора. Для механизмов приборов это, прежде всего, силовые погрешности: - силы и моменты трения в опорах, направляющих и шарнирных соединениях; - силы и моменты от неуравновешенности подвижной системы; - силы и моменты от взаимодействия подвижной системы с внутренними магнитными и электрическими полями; - аэродинамические, гидродинамические силы и моменты, возникающие при обтекании подвижной системы воздушными или газовыми потоками; - гидростатические силы (при расположении подвижной системы жидкости) и т.п. Для электронных и электромеханических цепей источниками таких воздействий являются: - паразитные термо-ЭДС в соединениях разнородных проводников; - сопротивления утечек; - паразитные индуктивные и емкостные связи;

- внутренние шумы радиоэлектронных элементов и т.п. Погрешности рассматриваемого типа носят случайный характер.

Механизм влияния указанных факторов на погрешность проектируемого устройства заключается, как правило, в их воздействии на значения внутренних параметров. Так, например, повышение температуры вызывает изменение линейных размеров деталей, упругих свойств материалов, электрического сопротивления проводников и т.п., что в свою очередь приводит к изменению функции преобразования измерительного устройства и к появлению указанной составляющей погрешности. Если влияющие факторы изменяются в пределах, оговоренных нормальными условиями, то учет этих факторов производится на этапе расчета основной погрешности. Если изменения выходят за указанные пределы, то их учитывают при определении дополнительных погрешностей.