32Алгоритм проведения однократного измерения.

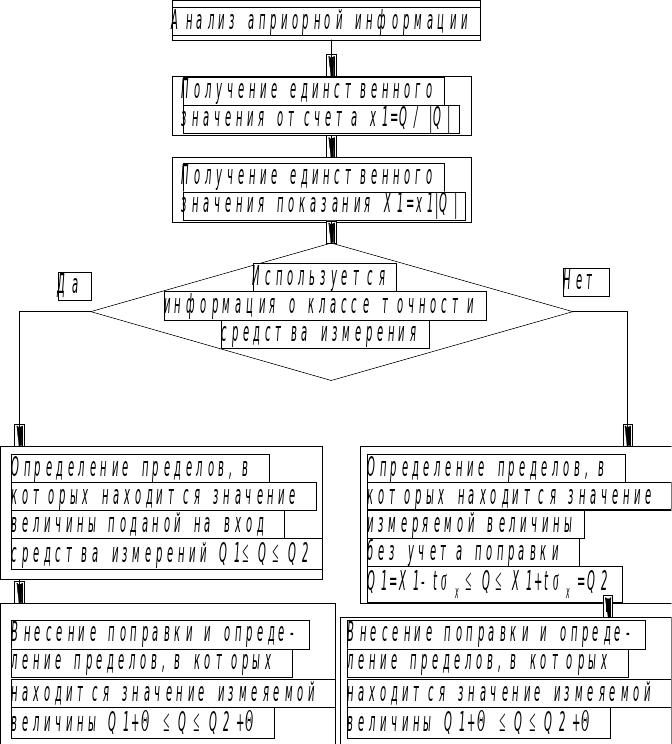
Однократное измерение заключается в реализации лишь одного сравнения неизвестной величины с единицей. Это наиболее распространенный, дешевый вид измерения и рекомендуется применять всегда, при условии соблюдения данной точности.

При проведении однократного измерения имеются следующие метрологические особенности: - из множества возможных случайных значений отсчета имеется только одно; - представление о законе распределения вероятности отсчета и среднеквадратическом отклонении формируется только на основе априорной информации.

Анализ априорной информации. Уточняются влияющие факторы и принимаются решения о путях снижения их влияния, принимается решение в пользу той или иной методики измерения, выбирается средство измерения и изучается его метрологическая хар-ка

Методика определения пределов, в которых лежит значение Q зависит от вида априорной информации. Рассмотрим три основных варианта:

– имеется информация о классе точности прибора, тогда где – предел допускаемой абсолютной погрешности, определяемой по классу точности;

– если известно, что результат измерения распределен по какому-то закону и известны значения оценок этого закона, то с заданной доверительной вероятностью находят доверительный интервал , - квантиль распределения, который определяют исходя из выбранной вероятности и вида закона распределения.

Если не известен вид закона распределения и нет информации о классе точности, то измерение однократное выполнять невозможно. Это будет противоречить второму постулату метрологии

Внесение поправок

или

Запись результатов измерений

или с дов. вер. p

33 Алгоритм проведения многократного измерения.

Многократное измерение выполняется в последовательности, показанной на алгоритме.

В результате анализа априорной информации определяются поправки к показанию. Затем производится n-независимых измерений. Измерения могут выполняться одним и тем же средством измерений, или несколькими, имеющими разную точность (многократные измерения с равноточными и неравноточными значениями отсчета).

Все значения отсчета переводятся в значения показания. После внесения в них поправок получается массив экспериментальных данных, представляющих собой n-независимых значений результата измерения. Среди этих значений могут быть ошибочные, происхождение которых не связанно со стохастической природой результата измерения. Исключение ошибок производится по определенным правилам (правило «трех сигм» или ν-критерий)

Главным при многократном измерении является эффективное использование апостериорной информации. Анализ ее начинается с выдвижения и проверки гипотез относительно закона распределения вероятности результата измерения. Гипотезы выдвигаются с учетом априорной информации, либо на основании рассмотрения гистограммы. Иногда по виду гистограммы можно с большой уверенностью сказать, что результат измерения подчиняется или не подчиняется нормальному закону.

Проверка гипотез осуществляется с помощью критериев согласия. При n>40…50 можно пользоваться критерием Пирсона. Согласно этому критерию за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерения принимается сумма квадратов отклонения частостей m_i/n от теоретических вероятностей P_i попадания отдельного значения результата измерения в i-ый интервал, причем каждое слагаемое берется с весовым коэффициентом n/P_i: , где k соответствует числу интервалов. Если расхождение случайно, то подчиняется хи-квадрат распределению Пирсона. Функция распределения, как известно, определяет вероятность того, что случайное число примет значение, меньшее аргумента этой функции. Поэтому, задавшись значением функции распределения Пирсона можно проверить, больше или меньше ее аргумента вычисленное значение. Если меньше, то с выбранной вероятностью можно считать аргумент случайным числом, подчиняющимся хи-квадрат распределению Пирсона, т.е. признать случайным расхождение между эмпирической и теоретическими плотностями вероятности результата измерения. Если больше аргумента вычисленное значение, то с той же вероятностью придется признать, что гипотеза о соответствии эмпирического закона распределения вероятности теоретическому не подтверждается.

Незнание закона распределения даёт в 2 раза менее точный результат.