9

29 Метрологические характеристики средств измерений: сущность, классификация, нормирование погрешности.

Метрологические характеристики средств измерений – это характеристики, определяющие результат и точность измерения. Различают следующие группы метрологических характеристик.

ГРУППА 1. Характеристики, предназначенные для определения результата измерения.

1. Функция преобразования – это функциональная зависимость между установившимися значениями выходного и входного сигнала (X,Y).

Она может быть представлена в трех видах: аналитическая зависимость Y=f(X); графическое представление; таблица значений X,Y. Градуировочная характеристика-то же, но получ.эксперимент

2. Цена деления шкалы – это разность значений измеряемой величины, которые соответствуют двум соседним делениям шкалы.

3. Длина деления шкалы – это расстояние между центрами (осями) двух соседних делений шкалы. Цена деления шкалы принимается большей, чем абсолютная погрешность измерительного прибора.

4. Диапазон измерений – это область значений измеряемой величины, в пределах которой измерительный прибор имеет нормированные метрологические характеристики.

5. Диапазон показаний – это область значений измеряемой величины, в пределах которой можно получить отсчет. Отсчет – это показания шкалы. От результата измерений отличается тем, что результат измерений содержит погрешность.

6. Пределы измерений (показаний) – это наибольшее и наименьшее значение диапазона измерений (показаний).

7. Чувствительность средств измерений – это отношение приращения выходного сигнала к вызвавшему это приращение, приращение входного сигнала.

8. Порог чувствительности – это наименьшее приращение входного сигнала, которое может быть зафиксировано обычным для средства измерительным способом.

ГРУППА 2. Метрологические характеристики чувствительности средств измерения к влияющим факторам. Результат измерений формируется под влиянием различных факторов(климатич,мех,)Примером для данной группы является функция влияния температуры.

ГРУППА 3.Характеристики погрешностей средств измерения.

1.Абсолютная погрешность – разность между показаниями прибора и значением измеряемой величины. Х=Хизм-Хист. Результат измерений Х=Х Х.Если нормируется предел абсолютной погрешности: , то это означает, что нигде в пределах диапазона погрешность средства измерения не превышает . При таком нормировании класс точности обозначается римскими цифрами или заглавными буквами латинского алфавита (например, М, С и т.д.).

2.Относительная погрешность – это отношение абсолютной погрешности к значению измеряемой величины: . В отличие от абсолютной погрешности, относительная погрешность – величина безразмерная. Относительная погрешность – это процент от показания. Если нормируется предел допускаемой относительной погрешности, то это означает, что нигде в пределах диапазона относительная погрешность не превышает %: .

При таком нормировании класс точности обозначается арабскими цифрами из ряда: 1; 1,5 ;(1,6); 2 ; 2,5 ; (3); 4 ; 5; 6. Допускается, но не рекомендуется 1,6 ; 3 . Причем цифры могут быть умножены на 10^р, где р – целые числа: 1; 0; -1; -2;…На приборе обозначается данная цифра в кружочке. или через дробь.

3.Приведенная погрешность – это отношение абсолютной погрешности к нормирующему значению: . Приведенная погрешность – величина безразмерная, так же как и относительная может быть выражена в процентах. Если нормируется приведенная погрешность, то класс точности обозначается теми же цифрами, что и в случае относительной погрешности, но только без кружочка.

Нормирующее значение определяется видом шкалы прибора и значением диапазона измерения. Существует несколько возможных вариантов выбора нормирующего значения: шкала прибора является равномерной с нулем в начале, шкала равномерная с нулем в середине, шкала с условным нулем, шкала прибора является неравномерной.

ГРУППА 4. Динамические метрологические характеристики

Динамические метрологические характеристики – это характеристики, описывающие работу средства измерения в динамическом режиме. Динамический режим характеризуется изменением измеряемой величины за время измерения.

Поэтому, имеет место динамическая погрешность (-это разность между погрешностью средства измерения в динамическом режиме и его статистической погрешностью). Для описания динамических свойств используют 2 группы характеристик: полные и частные динамические характеристики. Для удобства принимают несколько (5) полных динамических характеристик. При этом каждая из них дает исчерпывающую информацию о свойствах средств измерения. Каждая из полных характеристик является достаточной и может быть получена из другой полной характеристики.

1 хар-ка. Дифференциальное уравнение – это уравнение, связывающее выходную величину с входной, которая включает в себя внутренние параметры измерительного устройства, функцию изменения входной величины, скорость, иногда ускорение этого изменения: ytf[x(t);q ,x (t),x(t)]

2 хар-ка. Передаточная функция – это отношение изображение выходного сигнала к изображению входного: W(P)= . Передаточная функция при переходе к статистическому режиму превращается в чувствительность.

3 хар-ка.Комплексный коэффициент преобразования. АФХ= Совокупность амплитудных и фазовых частотных характеристик: W(P) W(j,w)=P(w)+jD(w); |W(P)|= ; .

Зависимость модуля передаточной функции от частоты входного сигнала называют амплитудно-частотной характеристикой (АЧХ). Широко применяется при оценке динамических средств измерений. Фазочастотная характеристика – это зависимость угла запаздывания выходного сигнала по отношению к входному (ФЧХ).

4 хар-ка. Отклик системы на единичный скачок называется переходной характеристикой.

U( ) – это переходная характеристика для t-момента.

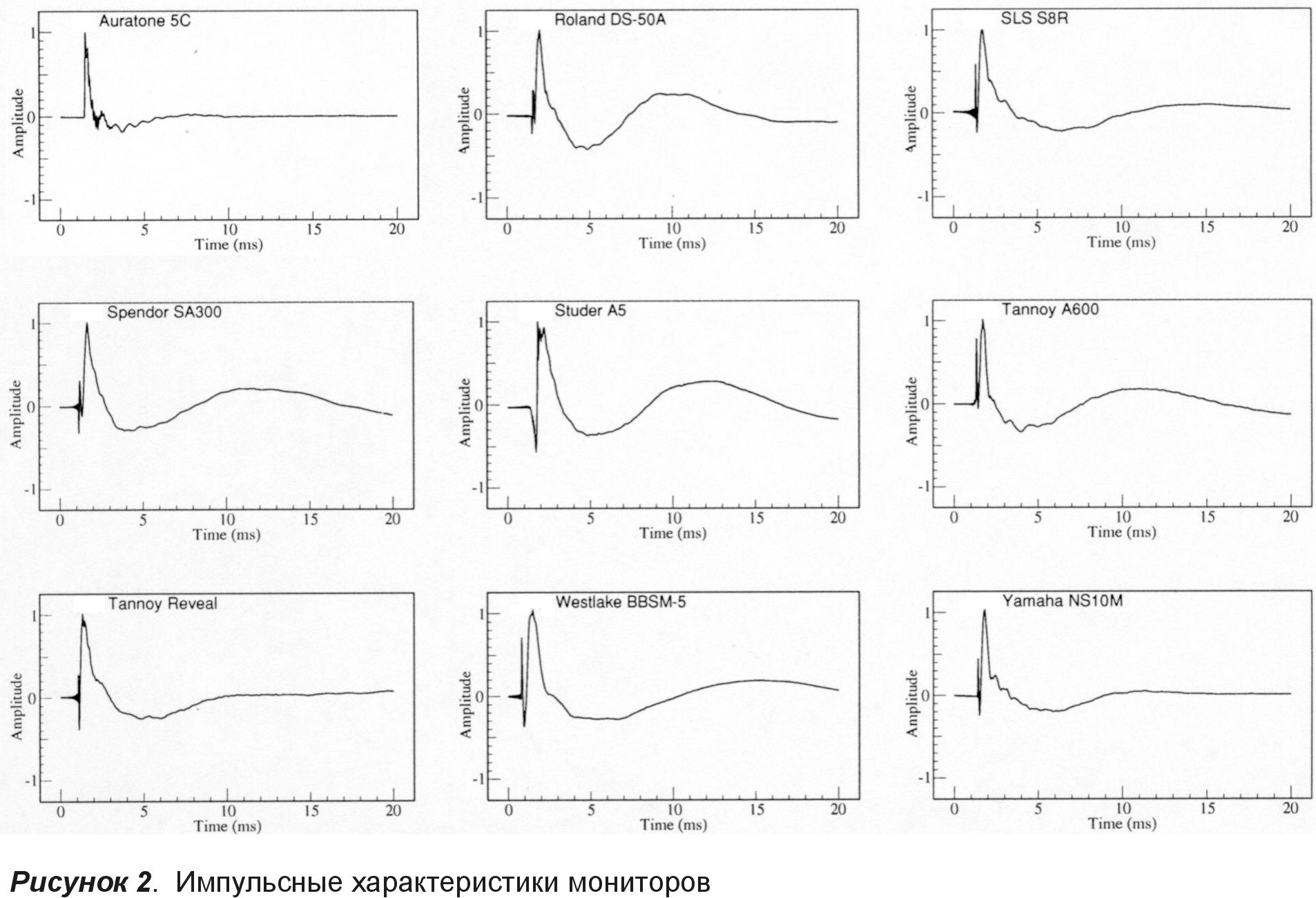5 хар-ка Отклик системы на единичный импульс – это импульсная или весовая функция.

Кроме полных широко применяются частные характеристики, которые не дают исчерпывающую информацию, но бывают наиболее удобны и характеризуют динамические свойства.