Нелинейный парный регрессионный анализ

При рассмотрении темы «Аппроксимация» отмечалось, что аппроксимацию табличных функций по методу наименьших квадратов называют также регрессионным анализом.

Линейный парный регрессионный анализ заключается в определении коэффициентов эмпирической линейной зависимости

, (1)

обеспечивающей аппроксимацию заданной табличной функции

, (2)

методом наименьших квадратов.

Это частный случай степенного полинома при его порядке . Коэффициенты полинома (1) можно определить, решив линейную систему уравнений 2-го порядка:

Эту систему можно решить аналитически:

; . (3)

Нелинейный парный регрессионный анализ заключается в определении пары коэффициентов и нелинейной относительно переменной аппроксимирующей функции

. (4)

Нелинейную парную регрессию можно свести к линейной при помощи линеаризующих преобразований аппроксимируемой табличной функции (2) и значений , , вычисляемых по формулам (3).

Пример. Пусть некоторую заданную табличную функцию (2) необходимо аппроксимировать нелинейной зависимостью

. (5)

Используем линеаризующее преобразование:

,

записав последнее выражение в виде:

.

Очевидно, что функция является линейной относительно переменной с коэффициентами

; . (6)

Таким образом, для того, чтобы применить к функции (5) формулы линейной регрессии (3), необходимо предварительно пересчитать исходную табличную функцию (2) в виде

; ,

и подставить в (3) вместо и соответственно и . После этого из (6) можно найти действительные значения , :

; .

Указанный алгоритм можно изобразить в виде блок-схемы, представленной ниже.

Таблица линеаризующих преобразований, сводящих нелинейную парную регрессию к линейной, представлена ниже.

Если вид эмпирической зависимости (4) заранее неизвестен, то целесообразно составить программу, которая вычисляла бы коэффициенты и , а также функционал для любой из функций, приведенной в таблице (этот список может быть расширен), и упорядочивала бы этот список по возрастанию суммы квадратов отклонений.

Таблица преобразований, сводящих нелинейную регрессию к линейной

ya(x)	yЛi	xЛi	d0	d1
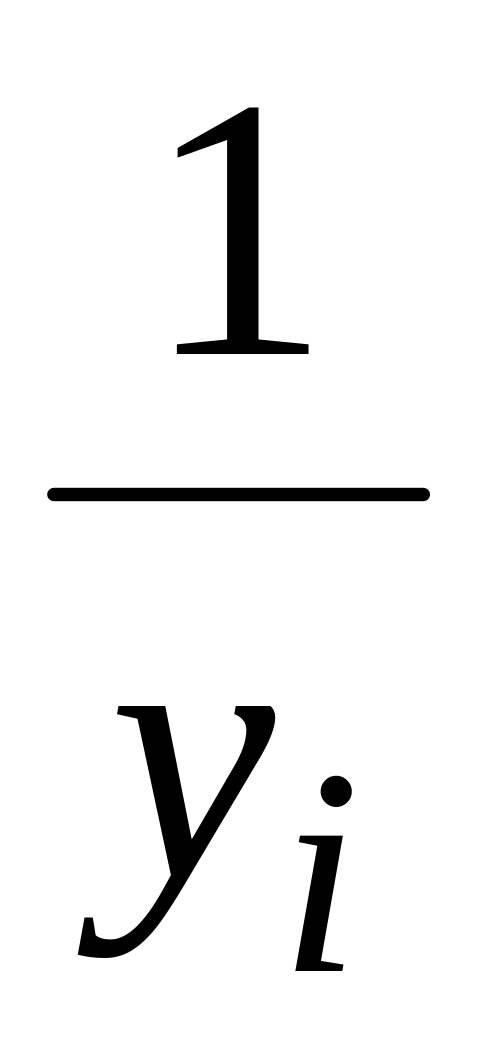
		xi	c0	c1
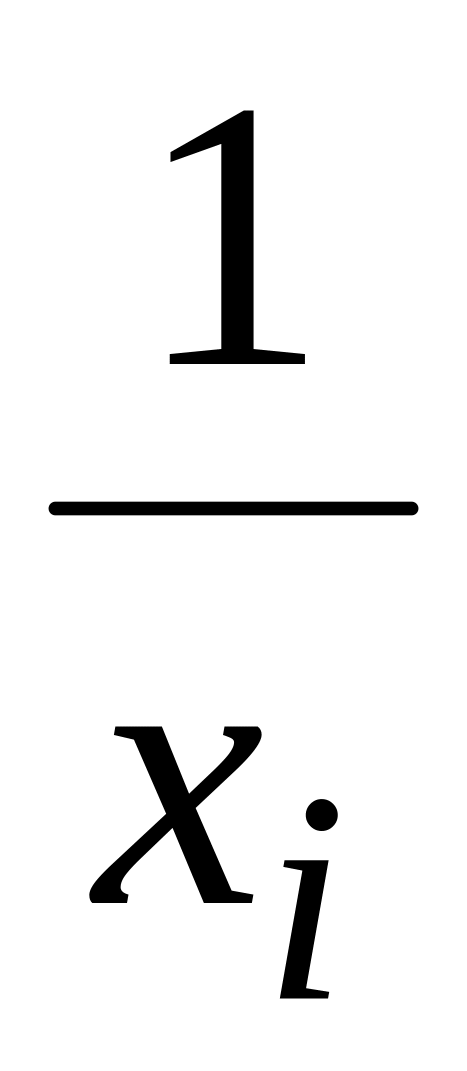
	yi		c0	c1
			c1	c0
		xi	c0	c1
		xi
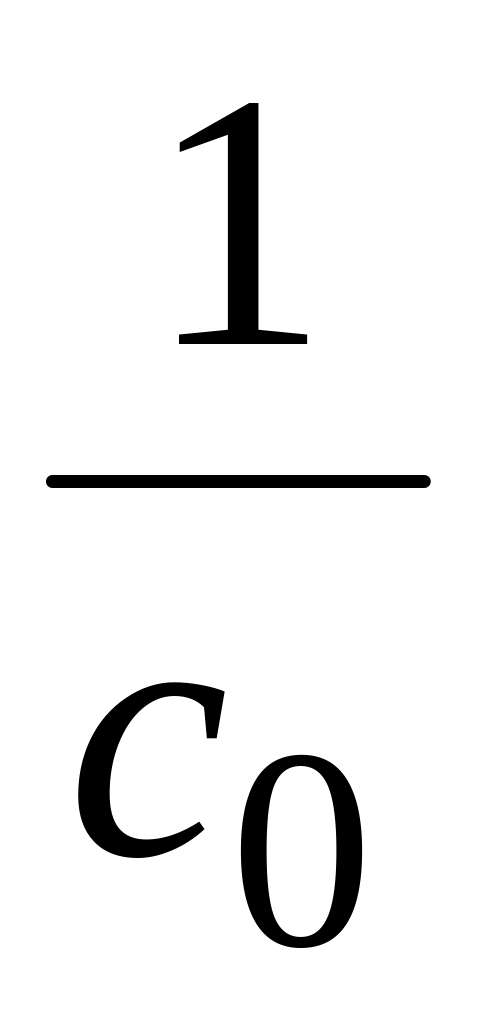
		xi
		xi
		xi
		xi		c1
				c1
		xi		c1
				c1
	yi		c0	c1
	yi		c0	c1
				c1
			c0	c1
	yi		c0	c1

Пример.

Аппроксимировать заданную табличную функцию

xi	–1	0	1	2	3
yi	–1,0	0,67	0,5	0,9	1,0

нелинейной аналитической зависимостью вида

.

Соответствующая Matlab-программа может иметь вид: