Операции со степенными полиномами

Понятие степенного полинома

Степенным многочленом (полиномом) (СП) n-го порядка называется функция вида:

.

Иногда СП записывают в несколько ином виде:

.

СП является наиболее удобной записью аналитического выражения, и поэтому наиболее часто используется при решении электротехнических задач на ЭВМ.

В Matlab используется первая форма записи СП, но нумерация коэффициентов начинается не с нуля, а с единицы:

Именно такая форма записи СП используется в дальнейшем.

Вектор – вектор коэффициентов СП (размерностью ); – порядок СП; – независимая переменная.

Вычисление значения полинома

В вычислительной математике доказано, что наиболее экономичным с точки зрения количества арифметических операций сложения и умножения является алгоритм вычисления значения СП по схеме Горнера¹ (1819), основанной на следующем представлении СП:

.

Алгоритм, реализующий такое вычисление, представлен ниже.

В Matlab для вычисления значения СП используется функция polyval(B,x), где B – вектор коэффициентов СП; x – значение независимой переменной (скаляр, вектор или матрица значений), в которых вычисляются значения СП. Результатом функции является матрица той же размерности, что и x.

» B=[2 5 0 -8 4];

» polyval(B,2)

ans =

60

Вывод степенного полинома

Вывод СП на экран в форме многочлена выполняет функция

print2str(v,char)

Функция из вектора коэффициентов v полинома формирует строку символов, описывающую многочлен в общем виде, используя символ char в качестве изображения независимой переменной.

» a=[1 0 -5 2 3];

» poly2str(a,'x')

ans =

x^4 - 5 x^2 + 2 x + 3

» [na, sa]=poly2str(a,'x')

na =

x^4 - 5 x^2 + 2 x + 3

sa =

24

Вывод на экран функции в виде частного двух СП с коэффициентами a (числитель) и b (знаменатель) (передаточная функция) выполняет функция

printsys(a,b,char)

которая формирует строку символов, изображая независимую переменную, используя символ char (по умолчанию char='s'). Порядок знаменателя должен быть не меньше порядка числителя.

» a=[2 4 -3 -1 0 7]; b=[4 2 6 9 -1 2 1];

» printsys(a,b,'x')

num/den =

2 x^5 + 4 x^4 - 3 x^3 - 1 x^2 + 7

-----------------------------------------------

4 x^6 + 2 x^5 + 6 x^4 + 9 x^3 - 1 x^2 + 2 x + 1

Арифметические операции над степенными полиномами

Сложение (вычитание) СП, заданных векторами коэффициентов u и v, может быть выполнено непосредственно, если СП имеют один порядок. Результатом является СП того же порядка с вектором коэффициентов, представляющего собой сумму (разность) вектором коэффициентов суммируемых полиномов.

» u=[5 6 -7 3 2];

» v=[3 0 2 -5 1];

» p=u+v;

» poly2str(p,'x')

ans =

8 x^4 + 6 x^3 - 5 x^2 - 2 x + 3

В случае же, когда порядок СП разный, вектор коэффициентов полинома, имеющего меньший порядок, должен быть дополнен нужным количеством нулей слева. Текст функции, реализующей сложение (вычитание) СП, может иметь следующий вид:

function y=polysum(u,v)

% Функция возвращает вектор коэффициентов полинома,

% являющегося суммой заданных полиномов с векторами

% коэффициентов u и v

nu=length(u); nv=length(v);

if nu<nv

u=[zeros(1,nv-nu) u];

elseif nu>nv

v=[zeros(1,nu-nv) v];

end

y=u+v;

Пример использования этой функции из командной строки:

» p=[1 2 3 5 0 6]; q=[5 4 1 2];

» poly2str(p,'x')

ans =

x^5 + 2 x^4 + 3 x^3 + 5 x^2 + 6

» poly2str(q,'x')

ans =

5 x^3 + 4 x^2 + x + 2

» s=polysum(p,q); % Сложение СП

» r=polysum(p,-q); % Вычитание СП

» poly2str(s,'x')

ans =

x^5 + 2 x^4 + 8 x^3 + 9 x^2 + x + 8

» poly2str(r,'x')

ans =

x^5 + 2 x^4 - 2 x^3 + x^2 - 1 x + 4

Умножение СП, заданных векторами коэффициентов, выполняется путем их почленного перемножения. Результатом умножения двух СП порядков n1 и n2 является СП порядка n1+n2.

Умножение СП может быть реализовано с помощью стандартной функции Matlab

p=conv(u, v)

Функция возвращает вектор коэффициентов СП p, полученный в результате перемножения заданных СП.

Пример.

» a=[1 2 0 5]; b=[2 3 1];

» conv(a,b)

ans =

2 7 7 12 15 5

» poly2str(conv(a,b),'x')

ans =

2 x^5 + 7 x^4 + 7 x^3 + 12 x^2 + 15 x + 5

Деление СП, заданных векторами коэффициентов, выполняется по правилу деления полиномов, и реализуется с помощью стандартной функции Matlab

[d, r] = deconv(u, v)

Функция возвращает вектор d коэффициентов СП, полученного в результате деления СП с вектором коэффициентов u на СП с вектором коэффициентов v, и вектор r коэффициентов СП, являющегося остатком от деления.

Пример.

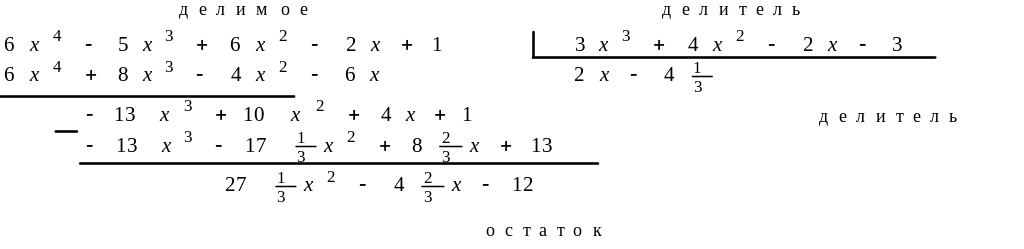
» a=[6 -5 6 -2 1]; b=[3 4 -2 -3];

» [d,r]=deconv(a,b);

» poly2str(d,'x')

ans =

2 x - 4.3333

» poly2str(r,'x')

ans =

27.3333 x^2 - 4.6667 x - 12

Вычисление корней степенного полинома

Вычисление корней трансцендентного уравнения вида

,

содержащего в левой части полином порядка с вектором коэффициентов p, выполняется с помощью функции

roots(p)

которая возвращает вектор корней СП.

» a=[2 5 6 -3 2];

» roots(a)

ans =

-1.5054 + 1.4281i

-1.5054 - 1.4281i

0.2554 + 0.4087i

0.2554 - 0.4087i

Определение коэффициентов СП по известному вектору корней x

выполняет функция

poly(x)

которая возвращает вектор коэффициентов СП, корни которого содержатся в заданном векторе x.

» x=[3 5 -1 2];

» poly(x)

ans =

1 -9 21 1 -30

» poly2str(ans,'x')

ans =

x^4 - 9 x^3 + 21 x^2 + x - 30

Дифференцирование степенных полиномов

Определение вектора коэффициентов b СП , определяющего производную СП с вектором коэффициентов a

выполняет функция

b=polyder(a)

Определение векторов p и q коэффициентов СП таких, что

по известным векторам коэффициентов a и b может быть выполнено в виде:

[p, q] = polyder(a, b)

» a=[5 4 -7 4 3];

» polyder(a)

ans =

20 12 -14 4

» b=[6 -2 -1 12];

» [p,q]=polyder(a,b)

p =

30 -20 19 184 105 -156 51

q =

36 -24 -8 148 -47 -24 144

» printsys(p,q,'x')

num/den =

30 x^6 - 20 x^5 + 19 x^4 + 184 x^3 + 105 x^2 - 156 x + 51

---------------------------------------------------------

36 x^6 - 24 x^5 - 8 x^4 + 148 x^3 - 47 x^2 - 24 x + 144