39. Принцип суперпозиции. Электрический диполь.

Если в данной точке пространства различные заряды создают электрические поля, напряженности которых , то результирующая напряженность: принцип суперпозиции поле

Результирующее поле определяется векторной суммой полей отдельно взятых зарядов. Работает в случае дискретно распределенного заряда.

В случае непрерывно распределенных зарядов:

, - направленность диффиренциально малого заряда

Электрический диполь – модель зарядной системы, состоящей из двух точечных зарядов, одинаковых по величине и противоположных по знаку, жестко связанных между собой.

, - электрический диполь

40. Поток вектора напряженности электрического поля. Примеры применения теоремы Остроградского-Гаусса.

П оток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

П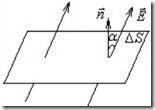 оток характеризуется числом линий, пронизывающих участок.

Поток – величина алгебраическая. Знак потока зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении Ф_Е. Изменение направления нормали на противоположное изменит знак E_n, а значит и знак потока Ф_Е. В случае замкнутых поверхностей принято считать знак потока положительным, если силовые линии поля выходят из охватываемой области наружу. Численно поток равен количеству силовых линий, пресекающих данную поверхность. Размерность потока в СИ: [Ф_Е] = В·м 

Теорема Остроградского-Гаусса: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности.

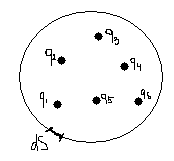
Е сли внутри замкнутой поверхности имеется несколько зарядов, то поток их результирующего поля, согласно принципу суперпозиции, будет равен:

Окружим точечный заряд q замкнутой сферической поверхностью радиуса r и вычислим поток электрического поля точечного заряда через эту поверхность: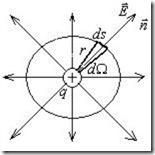

Мы видим, что полученный результат не зависит от формы и размеров выбранной поверхности. Это очевидно, поскольку поток численно равен количеству силовых линий, пересекающих данную поверхность, и в случае выбора замкнутой поверхности любой другой формы он не изменится, так как силовые линии нигде не прерываются.

Примеры применения теоремы Остроградского-Гаусса:

1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.

2. Электростатическое поле шара.

3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).

4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.

5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.

http://physics-lectures.ru/elektrostatika/13-8-primery-primeneniya-teoremy-gaussa/

// здесь эти примеры описаны более подробно.