3.1. Метод Коши

Описание алгоритма:

В методе Коши или методе наискорейшего спуска в качестве направления поиска выбирается направление антиградиента.

- градиент функции

Алгоритм метода выглядит следующим образом:

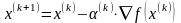, где - градиент.

Значение 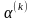на каждой итерации вычисляется путем решения задачи одномерного поиска экстремума вдоль направления градиента 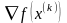. Если в качестве взять некоторое положительное число, то получится простейший градиентный алгоритм:

Одно из главных достоинств метода Коши является его устойчивость, так как всегда выполняется условие:

Однако вблизи экстремума скорость сходимости алгоритма становится недопустимо низкой, так как вблизи экстремума значение градиента стремится к нулю.

Алгоритм метода:

Шаг 1. Задать: 1. Начальную точку х⁽⁰⁾ ;

2. Условие окончания поиска. Перейти к шагу 2.

Шаг 2. Вычислить направление поиска в виде антиградиента функции

s(x^(k) ) = - ∇f(x^(k) );

. Перейти к шагу 3.

Шаг 3. Найти новое приближение

, где - величина шага относительно текущего приближения. Перейти к шагу4.

Шаг 4. Проверка условия окончания поиска.

Да: закончить поиск;

Нет: перейти к шагу 2.

Ход решения:

Исходные данные:

_{Шаг 1.}

- начальная точка (начальное приближение);

Вычислим компоненты градиента:

Шаг 2.

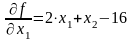
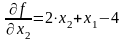
Шаг 3. Начальное приближение

1. Новое приближение определим по формуле:

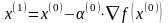
_{Шаг 2.}

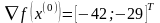
_{Находим} по аналогии с прошлым методом

_{Шаг 3.}

_{отсюда:} ; .

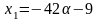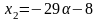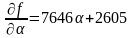. Приравняв его к нулю, находим ;

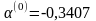_{2. Далее найдем точку:}

_{Шаг 2.}

_{Шаг 3.}

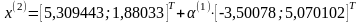
_{отсюда:} ; .

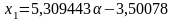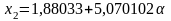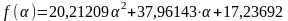
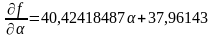. Приравняв его к нулю, находим

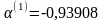
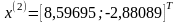
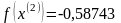
_{3. Далее найдем точку:}

Шаг 2.

Шаг 3.

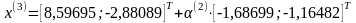
_{отсюда:} ; .

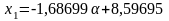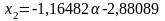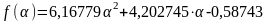
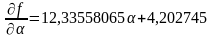. Приравняв его к нулю, находим

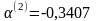
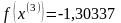
_{4. Далее найдем точку:}

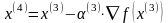
Шаг 2.

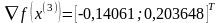
_{Шаг 3.}

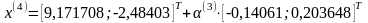
_{отсюда:} ; .

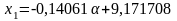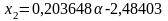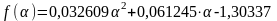
. Приравняв его к нулю, находим

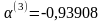
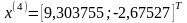
После 4 итераций найдено достаточно точное значение минимума, при котором значение целевой функции в точке , .

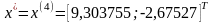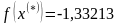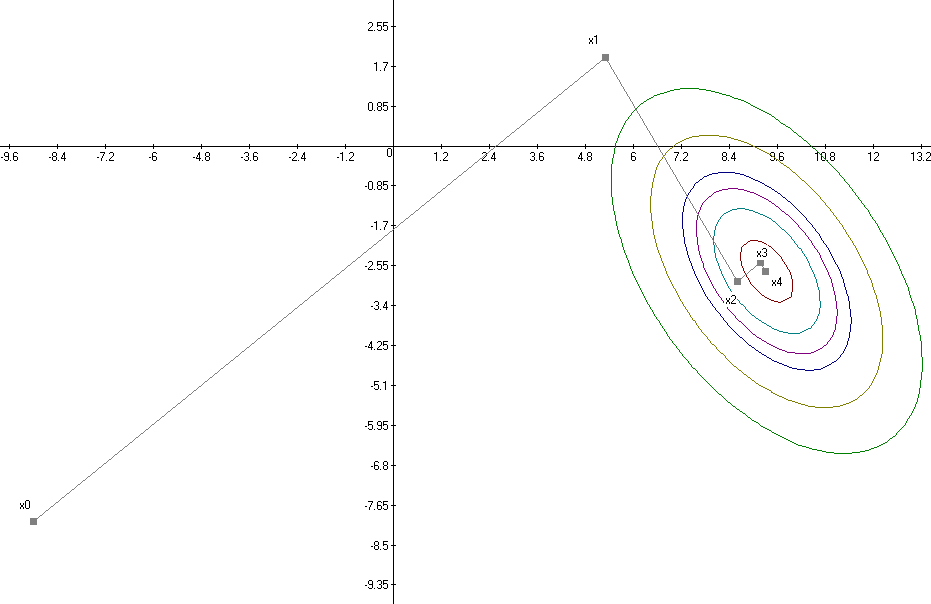
рис.5 Графическое пояснение метода Коши

3.2. Метод Ньютона

Описание алгоритма:

Этот метод использует информацию о вторых производных целевой функции. Эта информация появляется при квадратичной аппроксимации целевой функции, когда при её разложении в ряд Тейлора учитываются члены ряда до второго порядка включительно. Алгоритм метода выглядит следующим образом:

, где:

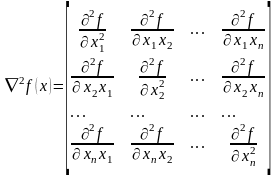- гессиан (матрица Гессе)

В случае, когда гессиан положительно определён, направление по методу Ньютона оказывается направлением спуска.

Алгоритм метода:

Шаг 1. Задать: начальную точку х⁽⁰⁾. Перейти к шагу 2.

Шаг 2. Вычислить направление поиска в виде

s(x^(k)) = –  .

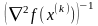
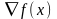Шаг 3. Найти новое приближение (являющееся решением задачи для квадратичной функции)

x^(k+1) = x^(k) + s(x^(k)) = x^(k) –  .

Шаг 4. Проверка на условие окончания вычислений.

Да: закончить процесс;

Нет: перейти к шагу 2.

Ход решения:

Исходные данные:

- целевая функция;

Шаг 1.

- начальная точка;

Шаг 2.

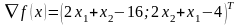
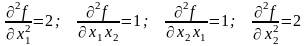
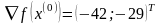
_{Шаг 3.}

;

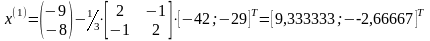
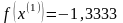
Таким образом, точка минимума , значение функции в которой найдена за одну итерацию.

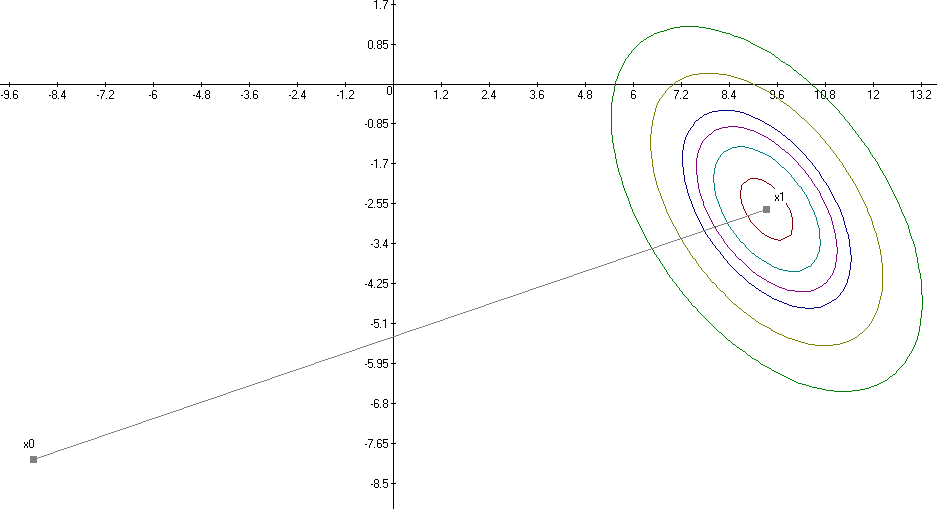
рис.6 Графическое пояснение метода Ньютона