
- •С одержание
- •Методы безусловной оптимизации
- •Нахождение стационарной точки
- •2.Методы прямого поиска безусловной оптимизации
- •2.1. Метод поиска по симплексу
- •2.2. Метод поиска Хука-Дживса
- •2.3. Метод сопряженных направлений Пауэлла
- •3.Нахождение безусловного экстремума градиентными методами
- •3.1. Метод Коши
- •3.2. Метод Ньютона
- •3.3. Метод сопряженных градиентов
- •3.4 Квазиньютоновский метод
- •Заключение.
- •Библиографический список:
2.2. Метод поиска Хука-Дживса
Описание алгоритма:
Процедура Хука-Дживса представляет собой комбинацию "исследующего" поиска с циклическим изменением переменных и ускоряющего поиска по найденному образцу. Исследующий поиск ориентирован на выявление направления вдоль "оврагов". Полученная в результате исследующего поиска информация используется затем в процессе поиска по образцу при движении по "оврагам".
Исследующий поиск:
Для проведения исследующего поиска необходимо задать величину шага, которая может быть различна для разных координатных направлений, и изменяться в процессе поиска. Поиск начинается в некоторой исходной точке. Делается пробный шаг вдоль одного из координатных направлений. Если значение целевой функции в пробной точке меньше, чем в исходной, то шаг считается удачным. В противном случае возвращаются в исходную точку и делают шаг в противоположном направлении. После перебора всех координат исследующий поиск заканчивается. Полученную в результате исследующего поиска точку называют базовой.
Поиск по образцу:
Поиск по образцу заключается в реализации единственного шага из полученной базовой точки вдоль прямой, соединяющей эту точку с предыдущей базовой точкой. Новая точка определяется по формуле:
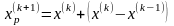
Как
только движение по образцу не приводит
к уменьшению целевой функции, точка
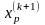 фиксируется в качестве временной базовой
точки и выполняется исследующий поиск.
При уменьшении значения целевой функции
эта точка рассматривается как базовая
точка. Если же исследующий поиск не дал
результата, необходимо вернуться в
предыдущую точку и провести исследующий
поиск заново. Если такой поиск не приводит
к успеху, то необходимо уменьшить
величину шага. Поиск завершается, когда
величина шага приращения становится
достаточно малой.
фиксируется в качестве временной базовой
точки и выполняется исследующий поиск.
При уменьшении значения целевой функции
эта точка рассматривается как базовая
точка. Если же исследующий поиск не дал
результата, необходимо вернуться в
предыдущую точку и провести исследующий
поиск заново. Если такой поиск не приводит
к успеху, то необходимо уменьшить
величину шага. Поиск завершается, когда
величина шага приращения становится
достаточно малой.
Алгоритм метода:
Шаг 1. Задать: 1. Начальную точку ;
2.
Приращение
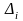 ,
,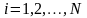 ;
;
3.
Коэффициент уменьшения шага
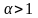 ;
;
4.
Параметр окончания поиска
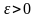 .
.
Шаг 2. Произвести исследующий поиск.
Шаг 3. Поиск удачный:
Да: перейти к шагу 5;
Нет: продолжить.
Шаг
4. Проверка на окончание поиска:
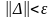 ?
?
Да: прекратить поиск;
Нет: уменьшить приращение по формуле:
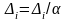 ,
;
Перейти к шагу 2.
,
;
Перейти к шагу 2.
Шаг 5. Провести поиск по образцу:
Шаг
6. Провести
исследующий поиск, используя
в качестве базовой точки:
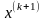 - полученная в результате точка
- полученная в результате точка
Шаг
7. Выполняется ли условие
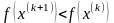 ?
?
Да:
продолжить
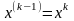 ;
;
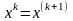 ;
;
перейти к шагу 5;
Нет: перейти к шагу 4.
Ход решения:
Исходные данные:
- целевая функция;
Шаг 1.
- начальная точка;
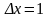 -
векторная величина приращения;
-
векторная величина приращения;
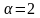 -
масштабный множитель;
-
масштабный множитель;
Минимизируем значение целевой функции до первого сокращения шага поиска
1.
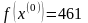
Шаг 2. Исследующий поиск вокруг базовой точки :
фиксируя , даём приращение переменной :
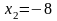 ;
;
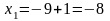 ;
;
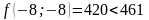 - поиск удачен;
- поиск удачен;
фиксируя , даём приращение переменной :
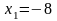 ;
;
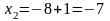 ;
;
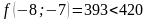 - поиск удачен;
- поиск удачен;
Шаг 3.
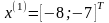
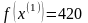
Так как поиск удачен, то переходим к поиску по образцу (Шаг 5):
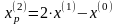
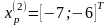
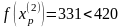
Шаг
6. 2.
Исследующий поиск вокруг точки
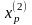 (Шаг
2.):
(Шаг
2.):
фиксируя , даём приращение переменной :
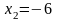 ;
;
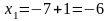 ;
;
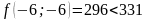 - поиск удачен;
- поиск удачен;
фиксируя , даём приращение переменной :
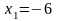 ;
;
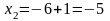 ;
;
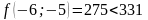 - поиск удачен;
- поиск удачен;
Шаг 7.
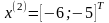
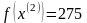
Шаг 5. Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.) :
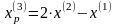
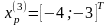
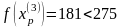
Шаг
6. 3.Исследующий поиск вокруг точки
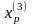 :
:
фиксируя , даём приращение переменной :
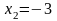 ;
;
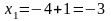 ;
;
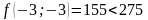 - поиск удачен;
- поиск удачен;
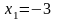 ;
;
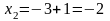 ;
;
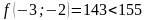 - поиск удачен;
- поиск удачен;
Шаг 7.
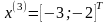
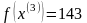
Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.):
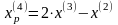
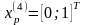
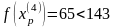
Шаг
6. Исследующий поиск вокруг точки
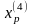 :
:
фиксируя , даём приращение переменной :
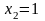 ;
;
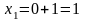 ;
;
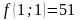 - поиск удачен;
- поиск удачен;
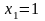 ;
;
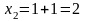 ;
;
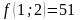 - поиск неудачен;
- поиск неудачен;
;
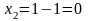 ;
;
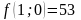 - поиск неудачен;
- поиск неудачен;
Шаг 7.
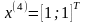
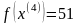
Шаг 5. Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.) :
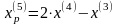

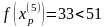
Шаг
6. Исследующий поиск вокруг точки
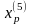 :
:
фиксируя , даём приращение переменной :
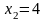 ;
;
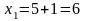 ;
;
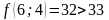 - поиск удачен;
- поиск удачен;
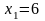 ;
;
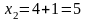 ;
;
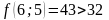 - поиск неудачен;
- поиск неудачен;
;
 ;
;
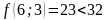 - поиск удачен;
- поиск удачен;
Шаг 7.
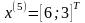
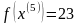
Шаг 5. Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.) :
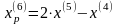
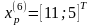
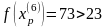
Значение целевой функции увеличилось, поэтому возьмём последнюю точку за временную базовую и проведём исследующий поиск (Шаг 6.):
Исследующий поиск вокруг базовой точки :
фиксируя , даём приращение переменной :
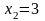 ;
;
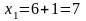 ;
;
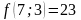 - поиск неудачен;
- поиск неудачен;
;
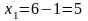 ;
;
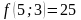 - поиск неудачен;
- поиск неудачен;
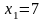 ;
;
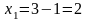 ;
;
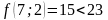 - поиск удачен;
- поиск удачен;
Шаг 7.
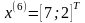
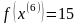
Шаг 5. Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.) :
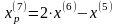
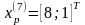
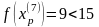
Шаг
6. Исследующий поиск вокруг точки
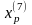 :
:
фиксируя , даём приращение переменной :
;
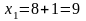 ;
;
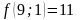 - поиск неудачен;
- поиск неудачен;
;
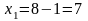 ;
;
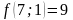 - поиск неудачен;
- поиск неудачен;
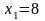 ;
;
;
;
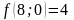 - поиск удачен;
- поиск удачен;
Шаг 7.
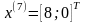
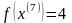
Шаг 5. Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.) :
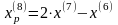
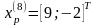
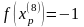
Шаг
6. Исследующий поиск вокруг точки
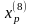 :
:
фиксируя , даём приращение переменной :
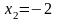 ;
;
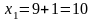 ;
;
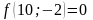 - поиск неудачен;
- поиск неудачен;
;
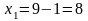 ;
;
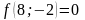 - поиск неудачен;
- поиск неудачен;
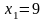 ;
;
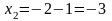 ;
;
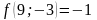 - поиск неудачен;
- поиск неудачен;
;
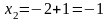 ;
;
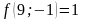 - поиск неудачен;
- поиск неудачен;
В
результате исследующего поиска не было
достигнуто уменьшение значения целевой
функции, то есть значение шага (векторной
величины приращения) уменьшить в
раз, до величины
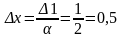 ,
затем необходимо произвести исследующий
поиск вокруг точки
,
затем необходимо произвести исследующий
поиск вокруг точки
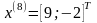 ,
используя новое значение приращения
,
используя новое значение приращения
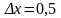 .
.
фиксируя , даём приращение переменной :
;
 ;
;
 - поиск неудачен;
- поиск неудачен;
;
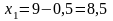 ;
;
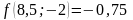 - поиск неудачен;
- поиск неудачен;
;
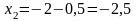 ;
;
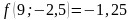 - поиск удачен;
- поиск удачен;
Шаг 7.
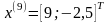
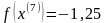
Шаг 5. Так как поиск удачен, то переходим к поиску по образцу (Шаг 5.) :
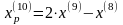
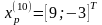
Значение целевой функции увеличилось, поэтому возьмём последнюю точку за временную базовую и проведём исследующий поиск (Шаг 6.):
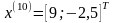
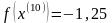
Исследующий поиск вокруг базовой точки :
фиксируя , даём приращение переменной :
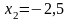 ;
;
;
;
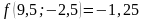 - поиск неудачен;
- поиск неудачен;
;
;
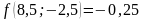 - поиск неудачен;
- поиск неудачен;
;
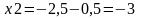 ;
- поиск неудачен;
;
- поиск неудачен;
;
 ;
;
 - поиск неудачен;
- поиск неудачен;
В
результате исследующего поиска не было
достигнуто уменьшение значения целевой
функции, то есть значение шага (векторной
величины приращения) уменьшить в
раз, до величины
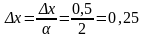 ,
затем необходимо произвести исследующий
поиск вокруг точки
,
затем необходимо произвести исследующий
поиск вокруг точки
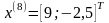 ,
используя новое значение приращения
,
используя новое значение приращения
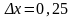 .
.
Итерации продолжаются, пока величина шага не укажет на окончание поиска в окрестности точки минимума.
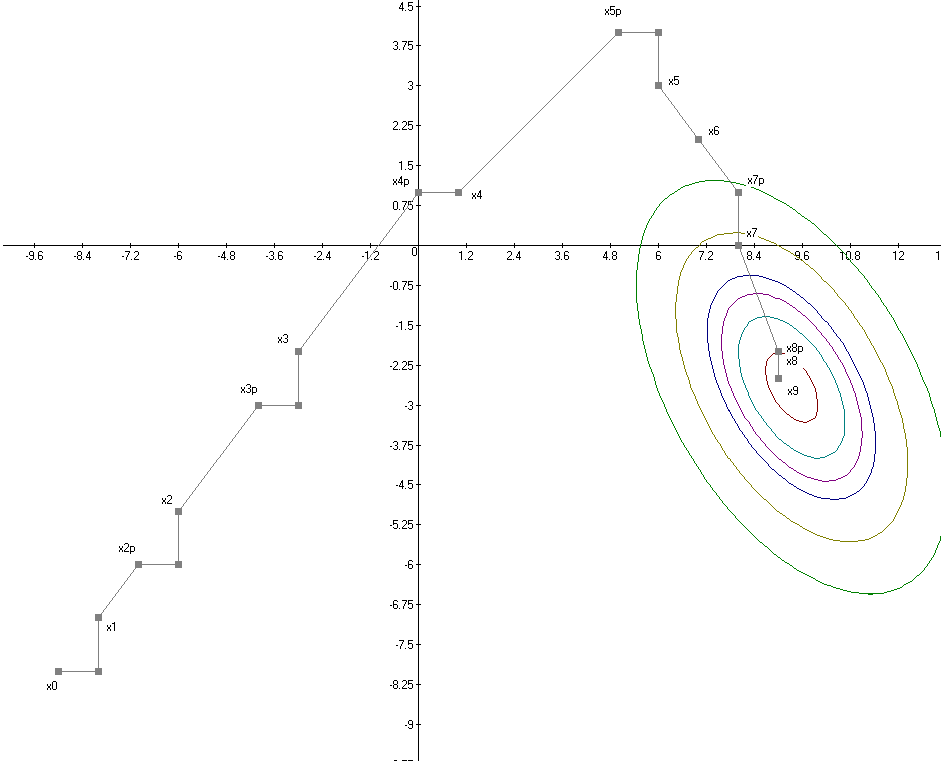
рис.3 Графическое пояснение метода Хука-Дживса
