ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Вечерне-заочный факультет

Кафедра автоматики и телемеханики

Пояснительная записка

курсовая работа по дисциплине

"методы оптимизации"

ТПЖА

Разработал студент:

Руководитель: к.т.н., доцент Микрюкова В.И.

Работа завершена с оценкой:

Члены комиссии:

Киров

2012 год

Задание на курсовую работу по дисциплине

"методы оптимизации".

ТЕМА: Методы безусловной оптимизации функции нескольких

переменных.

Студент: ____________ 10-УИ-522

1.Введение.

2.Исходные данные, нахождение стационарной точки.

3.Нахождение безусловного экстремума методами прямого поиска

3.1.Метод поиска по симплексу.

3.2.Метод поиска Хука-Дживса.

3.3.Метод сопряженных направлений Пауэлла.

4.Нахождение безусловного экстремума градиентными методами.

4.1.Метод Коши.

4.2.Метод Ньютона.

4.3.Метод сопряженных градиентов.

4.4.Квазиньютоновский метод.

5.Заключение.

руководитель работы: Микрюкова В.И.

задание принял:

С одержание

Введение……………………………………………………………………………..

1. Нахождение стационарной точки.....…………………………………………

2. Методы прямого поиска безусловной оптимизации....…………………….

2.1.Метод поиска по симплексу....…………………………………………….

2.2.Метод поиска Хука-Дживса................................................…………….

2.3.Метод сопряженных направлений Пауэлла......……………………….

3. Градиентные методы безусловной оптимизации……………………………

3.1. Метод Коши..............................................................................................

3.2Метод Ньютона........................................................................................

3.3.Метод сопряженных градиентов............................................................

3.4.Квазиньютоновский метод.......................................................................

4.Заключение……………………………………………………………………...

5.Библиографический список………....................……………………………..

Лист.

ТПЖА

Лист

Листов

Изм.

Лист

№ докум.

Подпись

Дата

4

Методы безусловной оптимизации

кафедра АТ

гр. УИ , 3 к., з/о

Введение

Оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Конечной целью оптимизации является отыскание наилучшего или "оптимального" решения.

Практика порождает все новые и новые задачи оптимизации причем их сложность растет. Требуются новые математические модели и методы, которые учитывают наличие многих критериев, проводят глобальный поиск оптимума. Реальные прикладные задачи оптимизации очень сложны. Современные методы оптимизации далеко не всегда справляются с решением реальных задач без помощи человека.

Оптимизационные методы минимизации и максимизации приобретают всё большую ценность и востребованность.

Методы оптимизации эффективно применяются в самых различных областях человеческой деятельности. Значительные успехи достигнуты при решении задач синтеза и анализа систем различного целевого назначения. Ускоренные темпы теоретических разработок в инженерную практику в существенной степени обусловлены широким распространением и совершенствованием средств вычислительной техники.

В настоящее время для инженера знание методов оптимизации также необходимо, как знание основ математического анализа, физики, радиоэлектроники и других дисциплин.

1. Нахождение стационарной точки

Целевая функция:

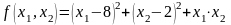
Для того, чтобы в точке 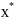функция f(x) имела безусловный локальный экстремум необходимо, чтобы все её частные производные обращались в точке в нуль.

Найдем для данной целевой функции 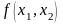частные производные

по 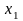и :

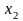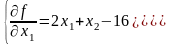
Приравняв полученные выражения к нулю, получим систему уравнений:

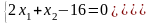
Решение системы уравнений даёт результат:

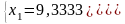
Таким образом, экстремум целевой функции является точка с координатами х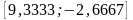^* = ^Т, значение целевой функции, в которой: .

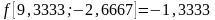Для определения характера стационарной точки составим определитель матрицы Гессе. Под определителем Гессе понимается определитель, составленный из вторых производных исходной целевой функции.

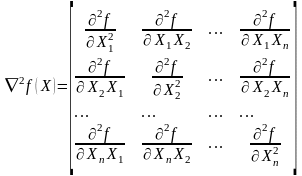
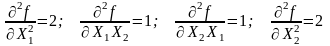
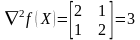
Так как гессиан функция - положительно определенная матрица (выполняются условия Сильвестра: все диагональные элементы матрицы Гессе - положительные величины, все ведущие главные определители положительные величины), стационарная точка является точкой минимума.

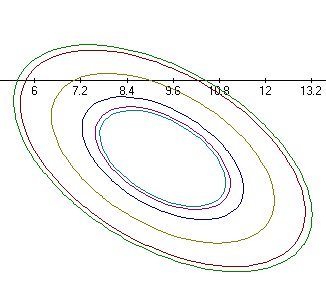
рис.1 линии уровня функции и точка экстремума x^*