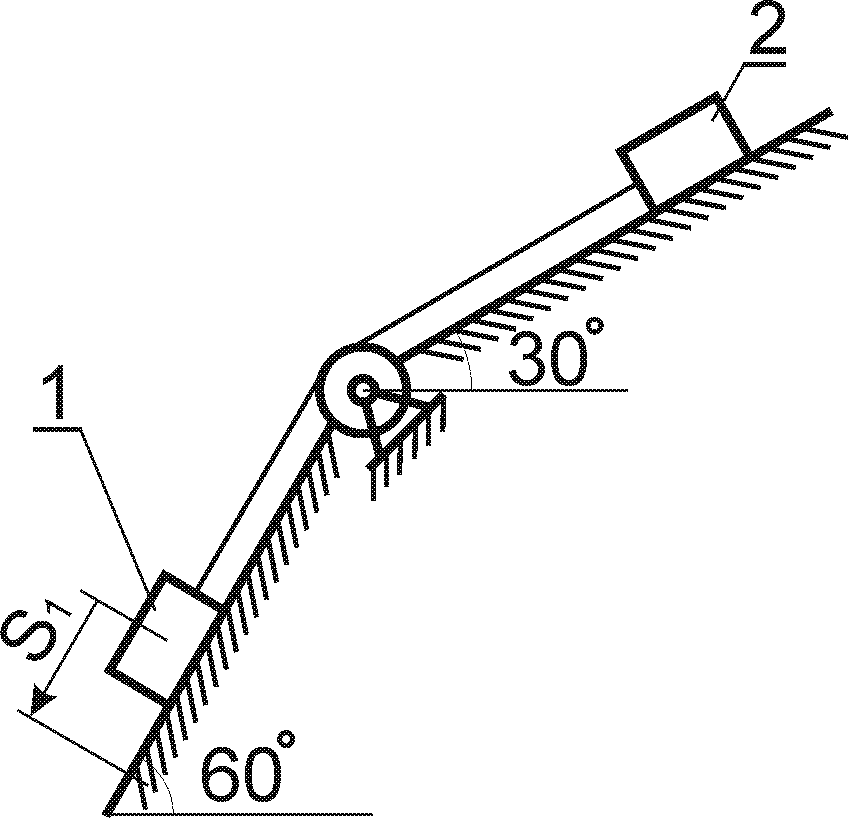
Дані для виконання завдання 4

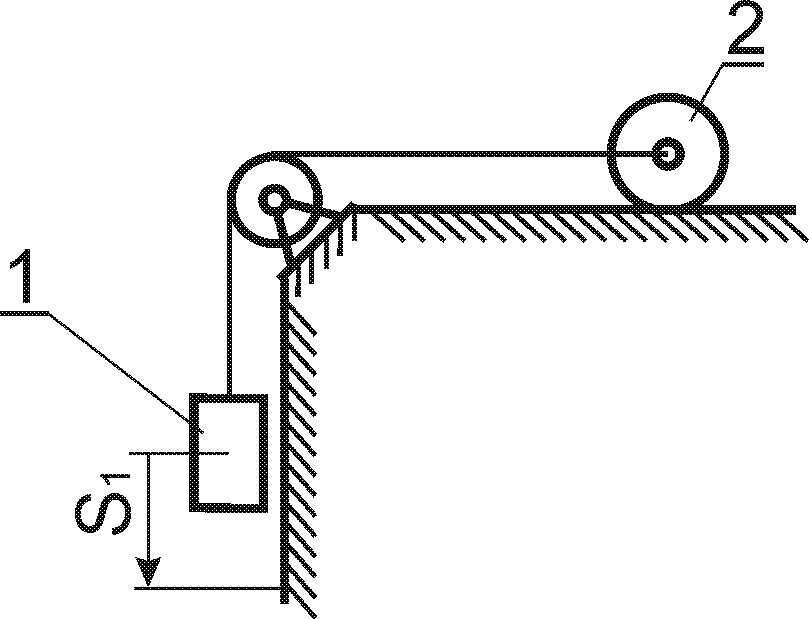
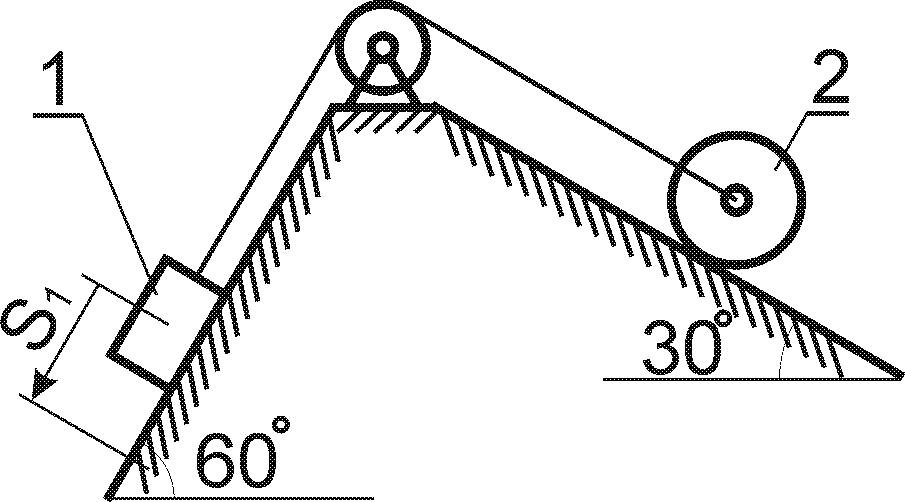
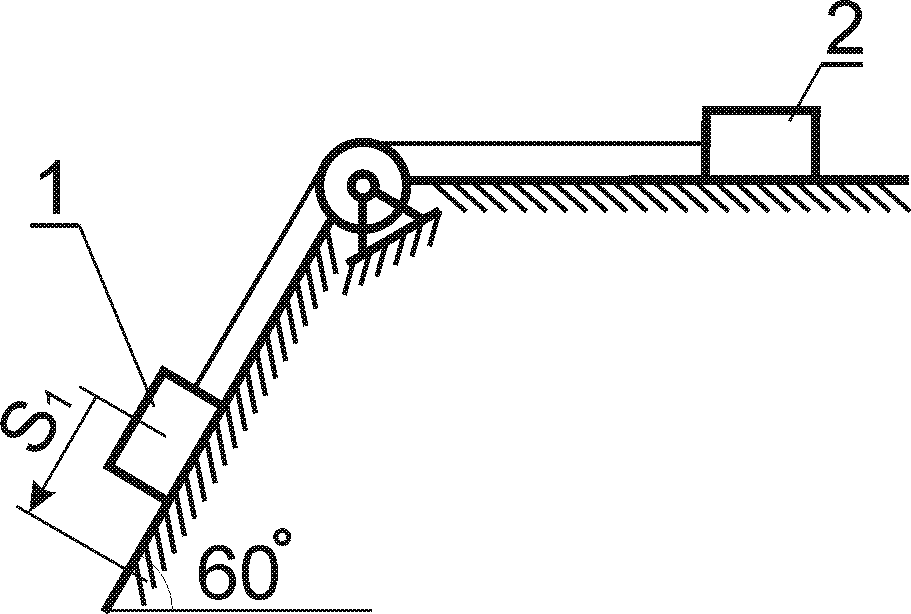
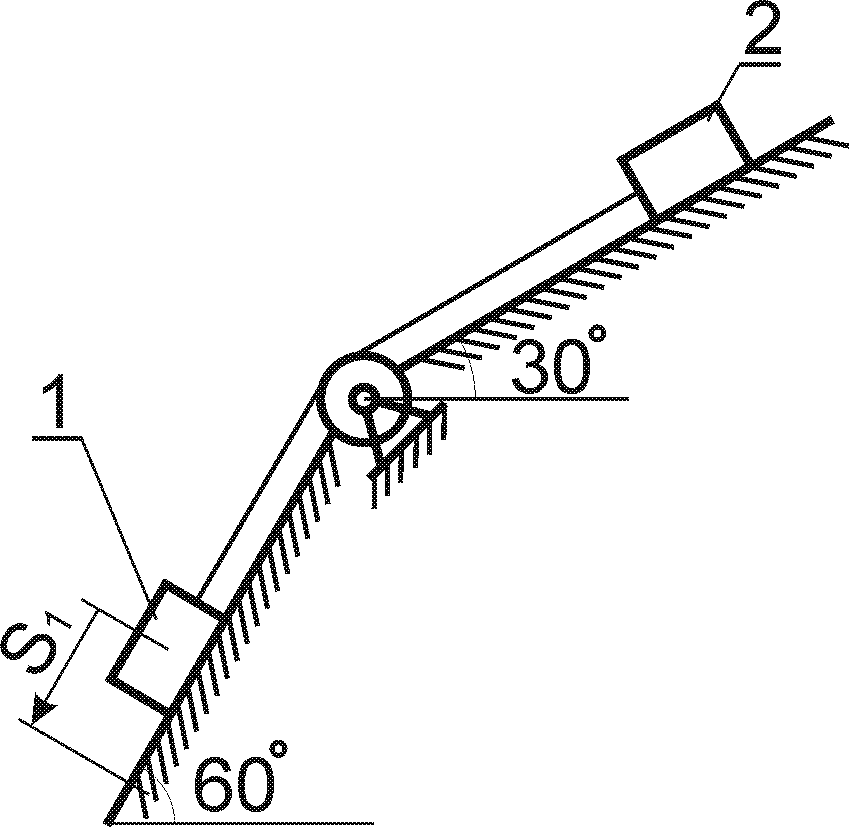
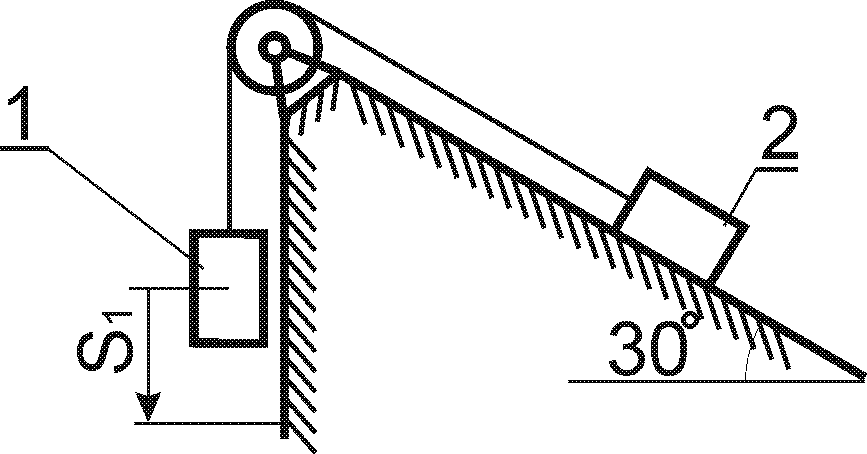
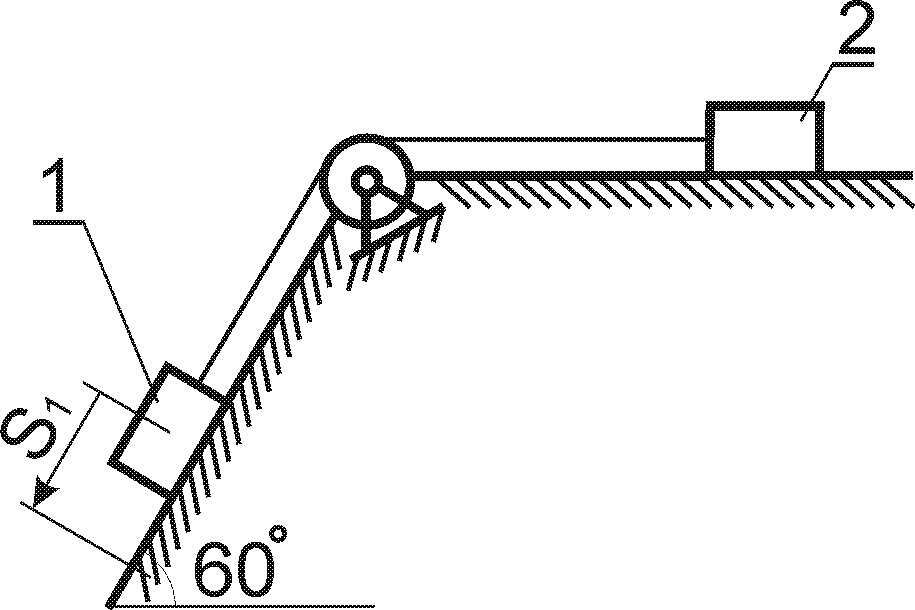
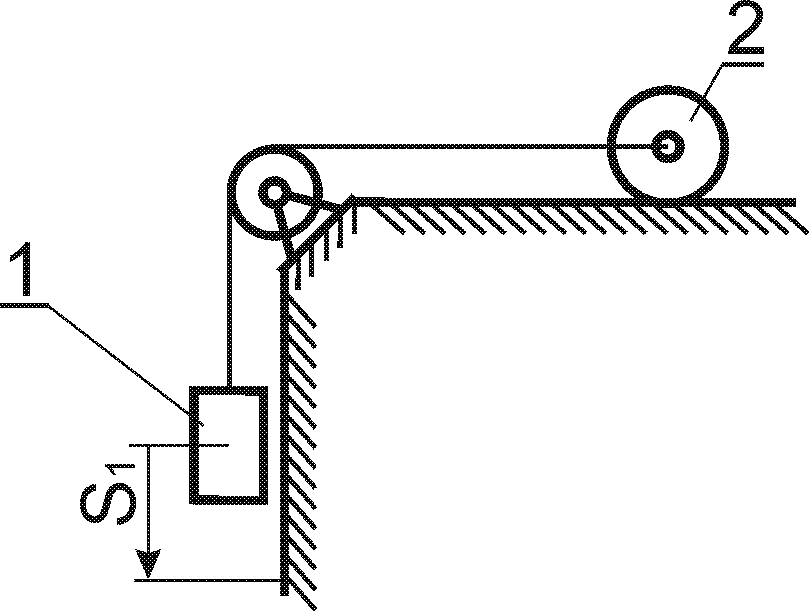
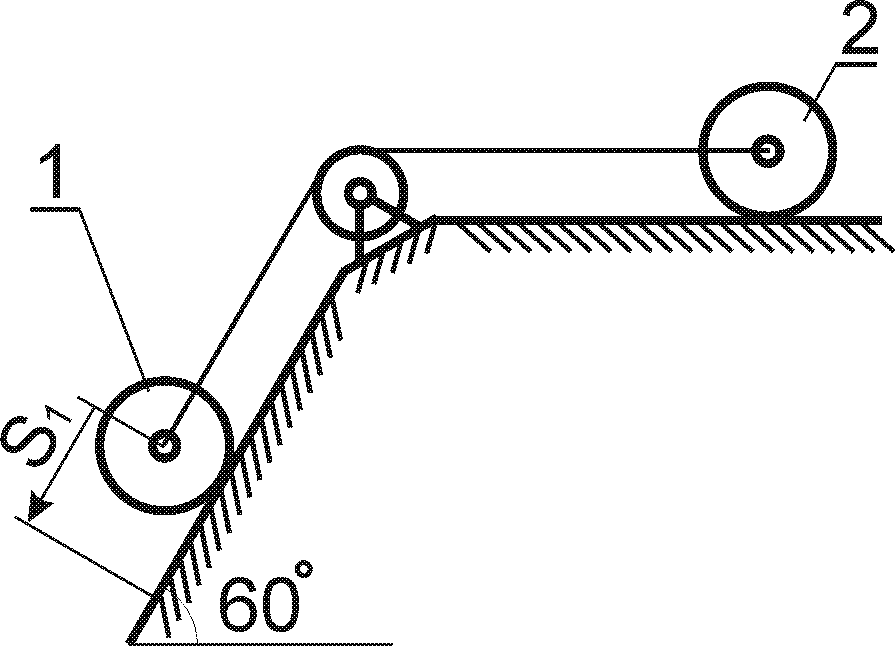
Варіанти кінематичних схем механізмів представлені рис.4.1.

Величини, необхідні для розрахунку, вибирають із табл. 4.

Таблиця 4

Дано	Передостання цифра шифру
	0	1	2	3	4	5	6	7	8	9
,м
, м	2,0	2,4	2,7	3,0	3,2	3,6	3,9	4,0	4,9	4,2
, м	0,32	0,34	0,36	0,38	0,4	0,42	0,44	0,46	0,42	0,36
, м	0,16	0,17	0,18	0,19	0,20	0,20	0,18	0,16	0,20	0,12
, м	0,08	0,09	0,1	0,12	0,14	0,12	0,1	0,08	0,07	0,06
, кг	200	250	300	350	400	350	300	250	200	180

Вказівки до послідовності виконання завдання

1. Визначаємо лінійну швидкість і прискорення вантажу в момент часу , коли він подолає задану відстань :

, .

2. Визначаємо кутову швидкість і кутове прискорення барабана, на який намотаний трос з вантажем (а отже, і колеса, що жорстко закріплено на одному валу разом із барабаном):

,

де – радіус барабана з індексом = 1,2,3 в залежності від варіанту завдання.

3. Згідно варіанту кінематичної схеми, визначаємо передаточне число , як відношення радіусів веденого колеса (кутова швидкість якого дорівнює кутовій швидкості барабана ) і ведучого колеса приводу.

4. Визначаємо кутову швидкість і кутове прискорення вала приводу, на якому закріплено колесо із заданою точкою :

.

5. Значення колової швидкості точки в момент часу розраховується за формулою:

де - радіус кола, по якому рухається точка .

6. Визначаємо лінійне прискорення точки , що має тангенціальну і нормальну складові:

,

Повне прискорення точки визначаємо за формулою:

,

7. Зображуємо знайдені вектори: швидкості – , тангенціального прискорення – , нормального прискорення – і повного прискорення – точки на кінематичній схемі механізму в певному масштабі.

8. Для визначення натягу троса використовуємо диференціальне рівняння руху вантажу. При цьому вважаємо, що до вантажу, як до матеріальної точки, прикладені дві протилежно спрямовані сили – сила реакції троса і сила тяжіння вантажу . Обираємо напрям осі у бік руху вантажу і в проекції на цю вісь складаємо диференціальне рівняння:

,

де – сума проекцій двох сил ( і ), які прикладені до вантажу, – прискорення вантажу.

Розв’язавши дане рівняння, знаходимо .

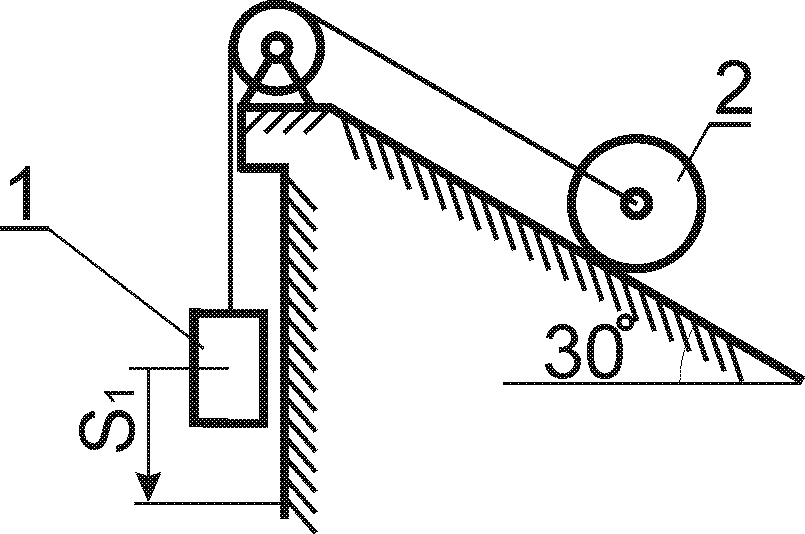
Приклад 4

Вантаж Р масою із стану спокою починає опускатись на тросі за допомогою механічного пристрою (рис. 4.2) згідно закону , де - відстань, яку пройшов вантаж від початкового положення (м), - час руху (с). В момент часу, коли вантаж пройде заданий шлях , визначити його швидкість і прискорення, а також кутову швидкість і кутове прискорення валів барабана і приводу, швидкість і прискорення точки М та натяг троса.

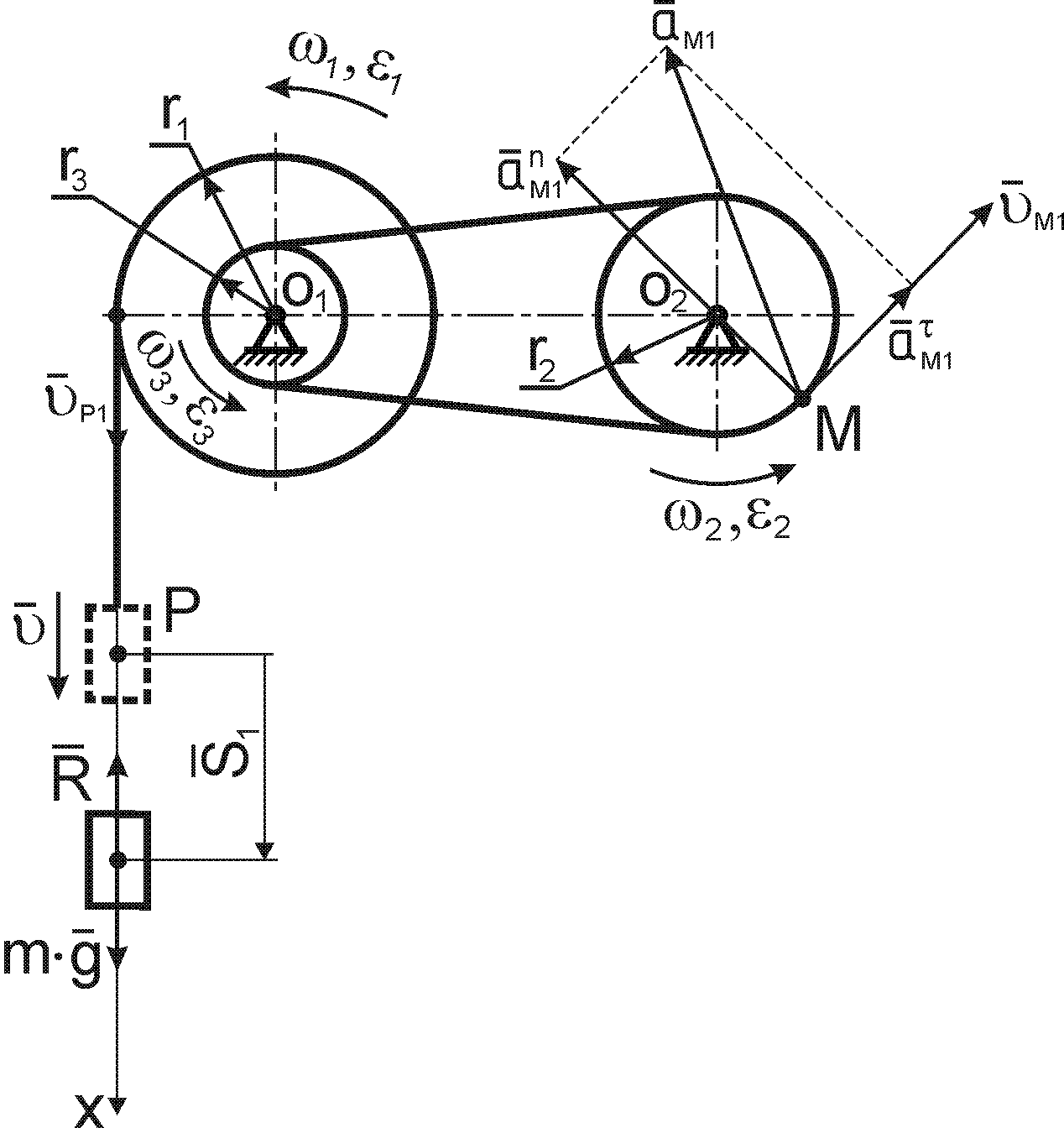
Рис. 4.2

Розв'язок

За умовою вантаж рухається поступально. Рівняння швидкості руху вантажу має вигляд:

.

Визначимо час, коли вантаж пройде шлях :

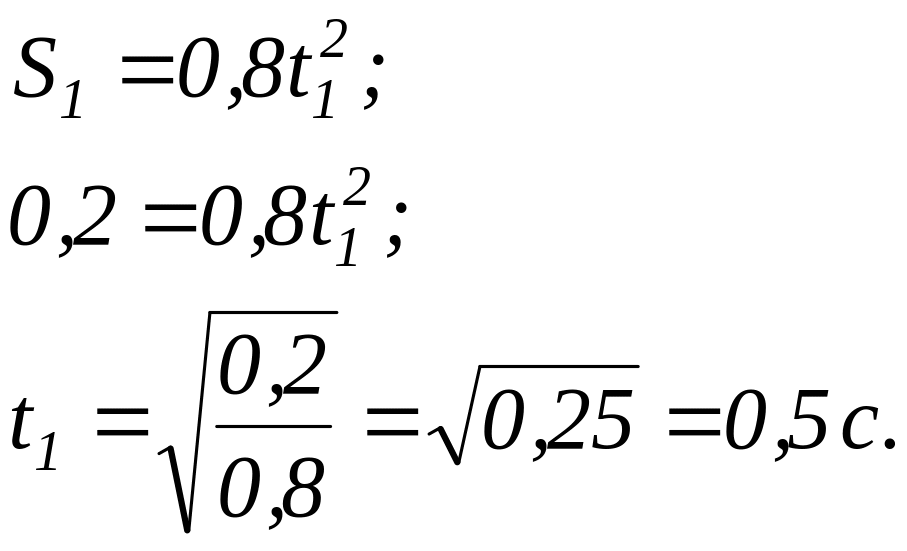
В момент часу швидкість вантажу буде дорівнювати

.

Прискорення вантажу :

.

В даному випадку прискорення вантажу не залежить від часу, тобто

.

При опусканні вантажу барабан 1 механічного пристрою буде обертатися із кутовою швидкістю , яка визначається:

,

де – колова швидкість точки на ободі барабана (ця швидкість дорівнює швидкості вантажу , так як за умовою задачі канат не розтягується), – радіус барабана 1.

Таку саму кутову швидкість буде мати колесо радіусом , оскільки воно жорстко з’єднано з барабаном і знаходиться з ним на одному валу:

,

Аналогічно можна визначити кутові прискорення барабана і колеса:

,

,

Передаточне відношення при передачі обертального руху в механічному пристрої від ведучого колеса 2 приводу до веденого колеса 3 визначається як:

Звідки можна знайти кутову швидкість і кутове прискорення вала приводу, на якому закріплено колесо 2:

В момент часу визначимо колову швидкість точки , яка знаходиться на ободі колеса 2:

,

де – радіус кола, по якому обертається точка .

Вектор швидкості спрямований по дотичній до колеса радіусом у бік його обертання.

Визначимо також для прискорення точки , знайшовши його тангенціальну і нормальну складові.

Тангенціальна складова прискорення точки буде дорівнювати:

.

Вектор прискорення спрямований по дотичній до колеса радіусом у бік вектора швидкості .

Нормальна складова прискорення точки дорівнює:

.

Вектор прискорення спрямований по радіусу до центра колеса 2.

Повне прискорення точки :

.

Напрямок вектора повного прискорення визначається із геометричної суми його складових:

.

Для визначення натягу троса замінемо зв’язок троса із вантажем реакцією , яка напрямлена вздовж троса протилежно зовнішній силі тяжіння . Такмм чином, будемо вважати вантаж матеріальною точкою, до якої прикладені дві протилежно спрямовані сили – сила реакції троса і сила тяжіння вантажу (рис. ).

Складемо диференціальне рівняння руху вантажу. Для цього оберемо напрям осі у бік руху вантажу, тобто вниз. В проекції на напрям руху вантажу будемо мати:

,

де – прискорення вільного падіння тіла, – прискорення вантажу.

Тоді

Таким чином, трос розтягується із зусиллям .

Завдання 5 - Теорема про зміну кінетичної енергії механічної системи

Механічна система складається з двох тіл 1 і 2 , які мають масу і відповідно та з'єднані між собою перекинутим через блок тросом (рис 5.1). Система рухаються із стану спокою. Визначити швидкість руху тіла 1 в момент часу, коли воно пройде відстань після початку руху.

При розв'язанні масою троса і блока знехтувати та припустити, що трос в процесі руху не деформується.

Радіус суцільного котка прийняти r= 0,2 м, коефіцієнт тертя ковзання шорсткої поверхні f = 0,2, коефіцієнт тертя кочення котка k = 0,01 м.

0	1
2	3
4	5
6	7
8	9

Рис. 5.1