Дані для виконання завдання 7

Варіанти розрахункових схем валів представлені рис.7.1.

Величини, необхідні для розрахунку, вибирають із табл. 7.

При розрахунках прийняти для матеріала валу (сталі) модуль пружності другого роду: G= 0,8·10⁵ Н/мм².

Таблиця 7

Дано	Передостання цифра шифру
	0	1	2	3	4	5	6	7	8	9
, кВт	9	10	11	12	13	13	10	9	8	7
, кВт	4	6	5	6	6	7	7	7	6	6
, кВт	3	3	4	4	5	5	5	4	4	3
,	200	220	240	260	280	300	280	260	240	220

Вказівки до послідовності виконання завдання

1. Визначаємо потужність , яка подається на трансмісійний вал:

2. Визначаємо обертальні моменти відповідно до потужностей :

,

де , рад/с – кутова швидкість обертання валу.

3. Креслимо ескіз валу і прикладаємо до нього знайдені зовнішні обертальні моменти .

4. Застосувавши метод перерізів, у відповідних поперечних перерізах валу по його довжині визначаємо крутні моменти , які дорівнюють алгебраічній сумі всіх зовнішніх моментів, прикладених по один бік розглядаємого перерізу. При цьому прймаємо наступне правило знаків: зовнішні моменти, діючі за годинником з боку розглядаємого перерізу частини валу, що лишилася, рахуються додатніми, діючі проти годинника – від’ємними.

5. Визначивши крутні моменти в поперечних перерізах на кожній ділянці валу, будуємо їх епюру в прйнятому масштабі . Слід відмітити, що в межах кожної ділянки значення крутного моменту переріза лишається постійним, а стрибки значень на епюрі відбуваються в точках прикладення зовнішніх моментів на величину зовнішнього момента.

6. Із умови міцності на кручення:

= ≤ ,

де -допустиме дотичне напруження, - максимальне значення крутного моменту на епюрі в поперечному перерізі бруса, = - полярний момент опору круглого поперечного перерізу бруса, визначаємо діаметр валу:

.

Приклад 7

На трансмісійний вал подається потужність , кВт при швидкості обертання і відповідно знімаються потужності з трьох шківів , , (рис. 7.2).

Визначити із умови міцності по дотичним напруженням діаметр валу, якщо допустиме напруження для його матеріалу .

Розв'язок

Потужність , яка подається на вал, дорівнює сумі потужностей, які з нього знімаються:

.

Кутова швидкість обертання валу дорівнює:

.

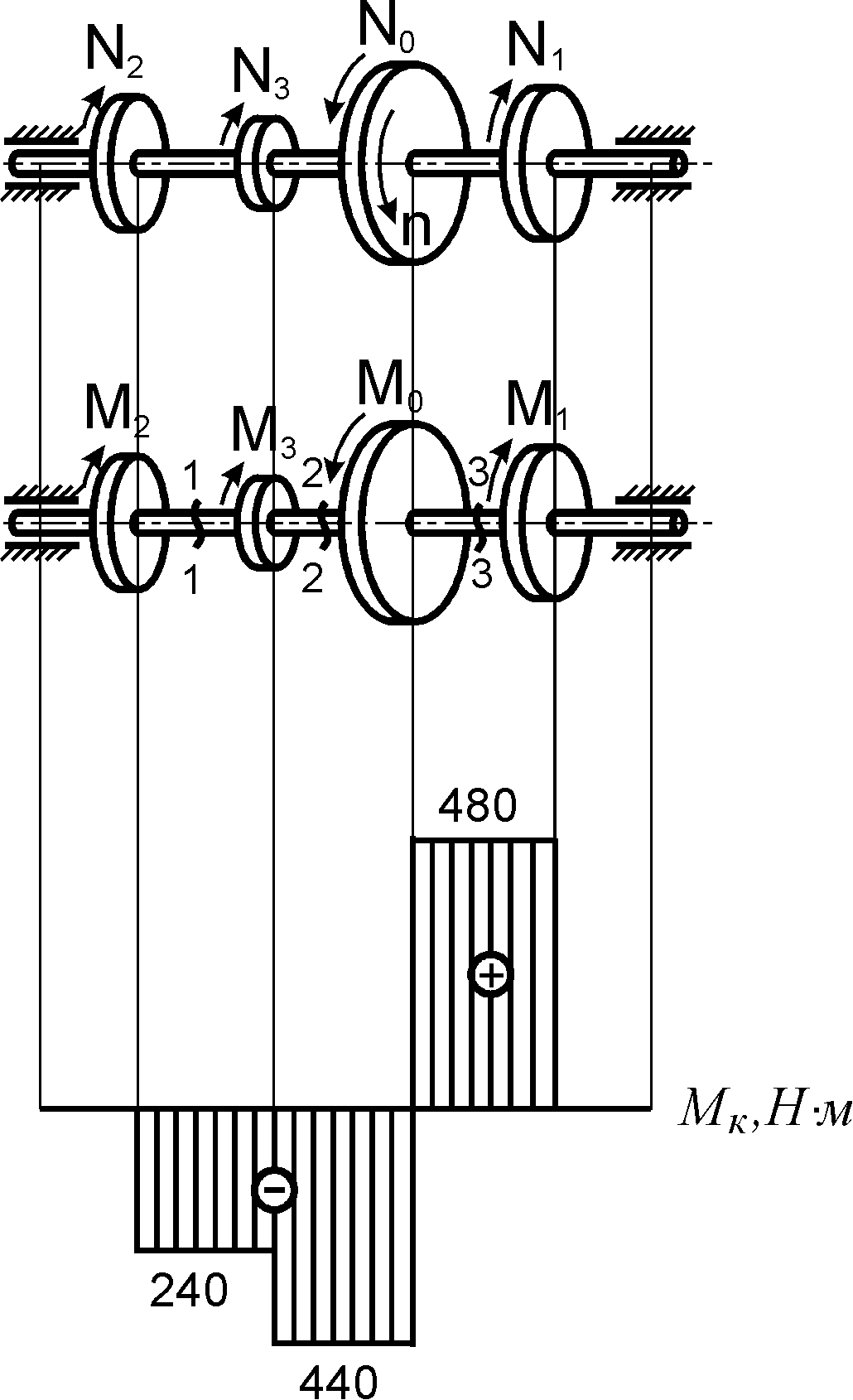
Рис. 7.2

Визначаємо обертальні моменти на шківах валу, які відповідають кожній потужності :

,

,

,

.

Зовнішній момент , що подається на шків валу має бути врівноважений сумою зовнішніх моментів, які знімаються з його шківів , , :

,

Побудуємо епюру крутних моментів (рис. 7.2).

Розбиваємо вал на три ділянки , , з межами в точках прикладання зовнішніх моментів. Визначимо крутні моменти в поперечних перерізах валу кожної ділянки, застосувавши метод перерізів. При цьому будемо складати рівняння рівноваги для лівої частини валу, відкинувши праву, і використовувати прийняте правило знаків для зовнішніх моментів, що діють на цю частину.

Тоді крутний момент в будь – якому перерізі першої ділянки валу дорівнює:

.

На другій ділянці :

На третій ділянці:

По знайденим величинам будуємо епюру крутних моментів, відкладаючи від нульової лінії у вибраному масштабі від’ємні значення вниз, а додатні – вгору. Аналогічні результати можна отримати, якщо будувати епюру зліва на право, розглядаючи рівновагу правої частини валу.

Діаметр валу із сталим перерізом визначаємо із умови міцності на кручення за максимальнимм значенням крутного моменту на епюрі:

,

де – максимамальний крутний момент на ділянці 3 валу.

Збільшуємо діаметр валу до найближчого більшого парного цілого значення .

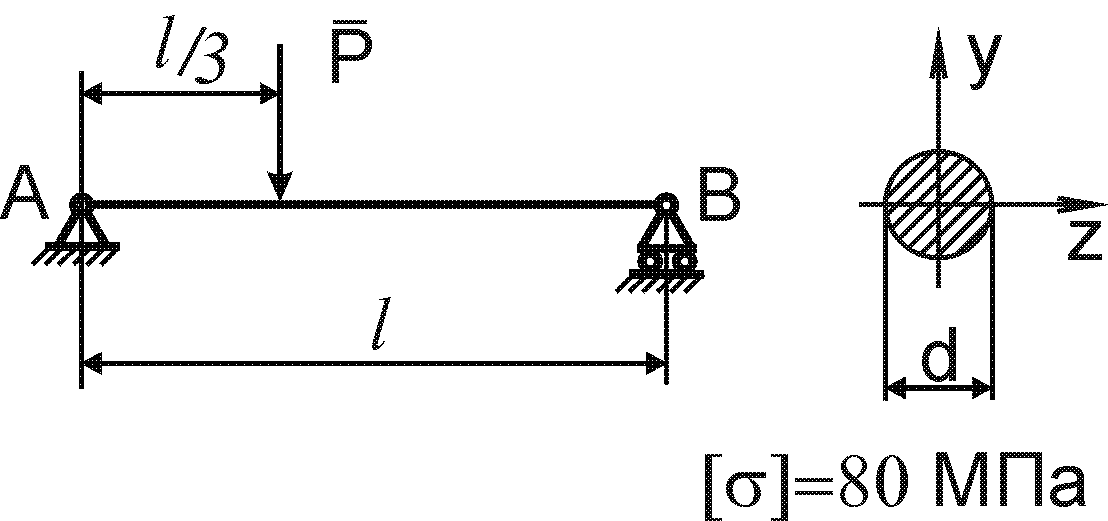
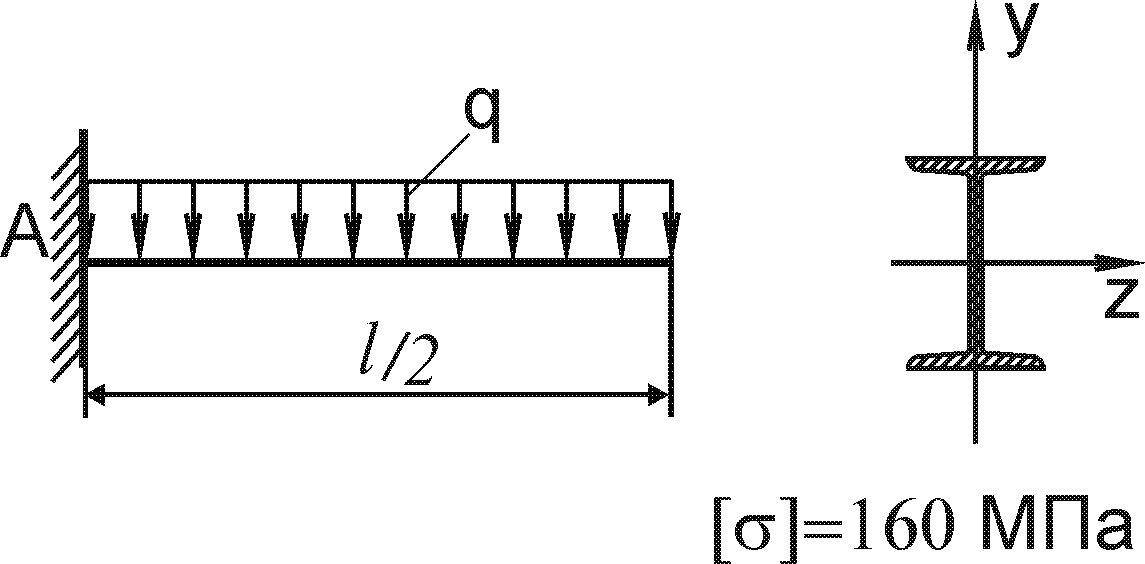
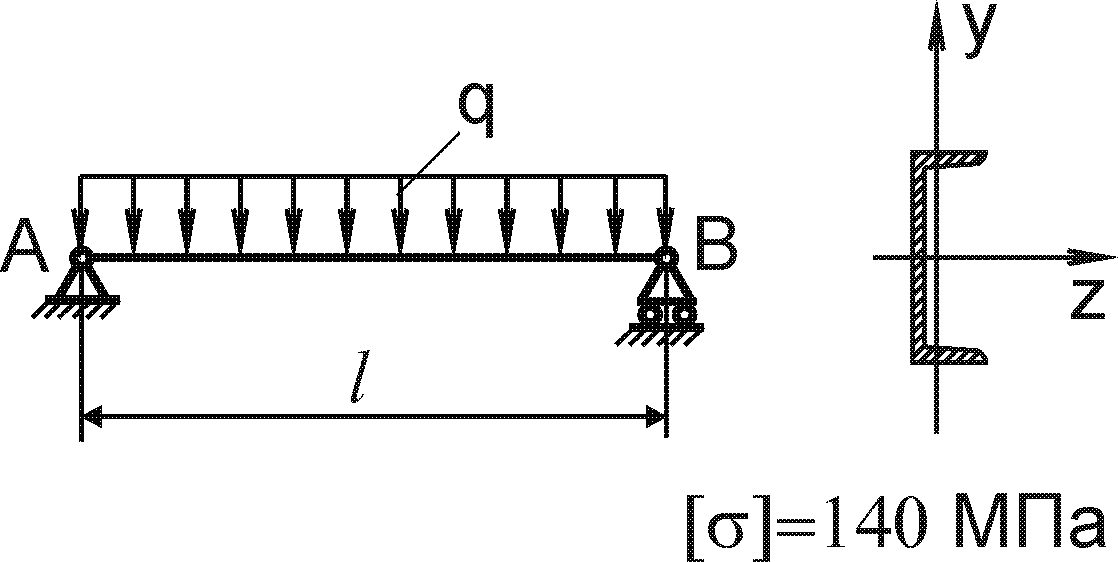
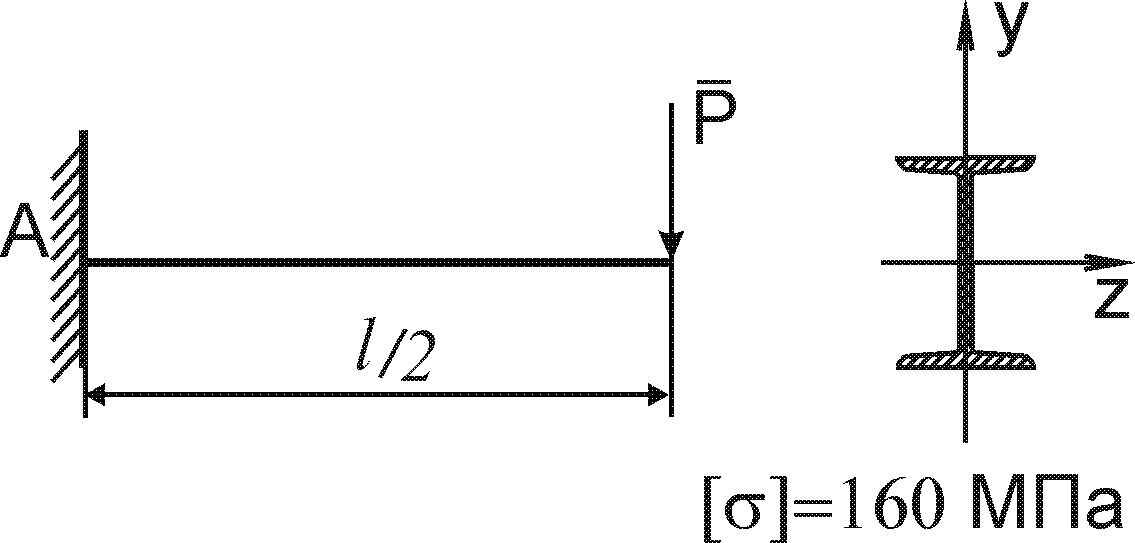
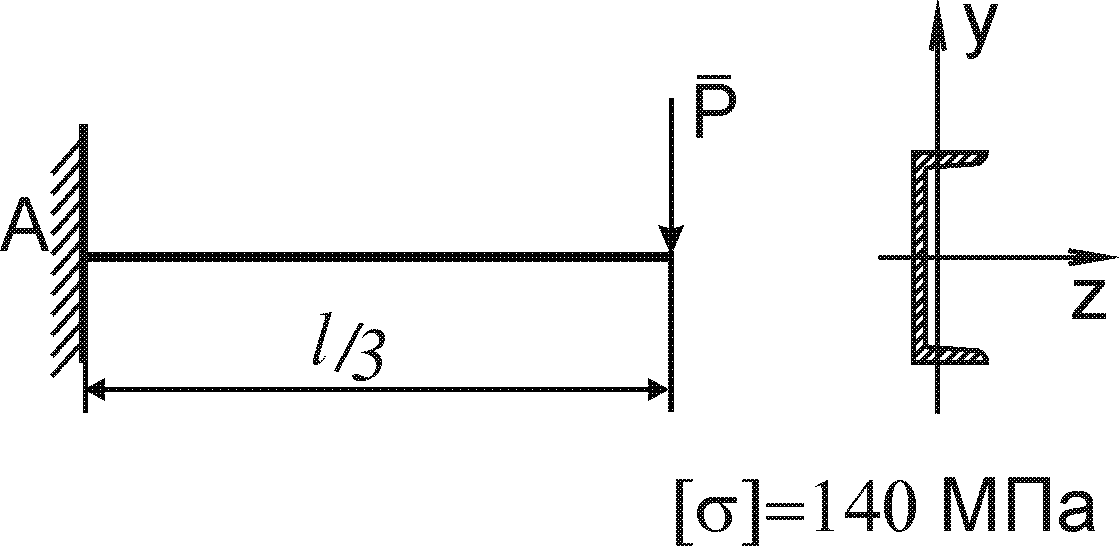
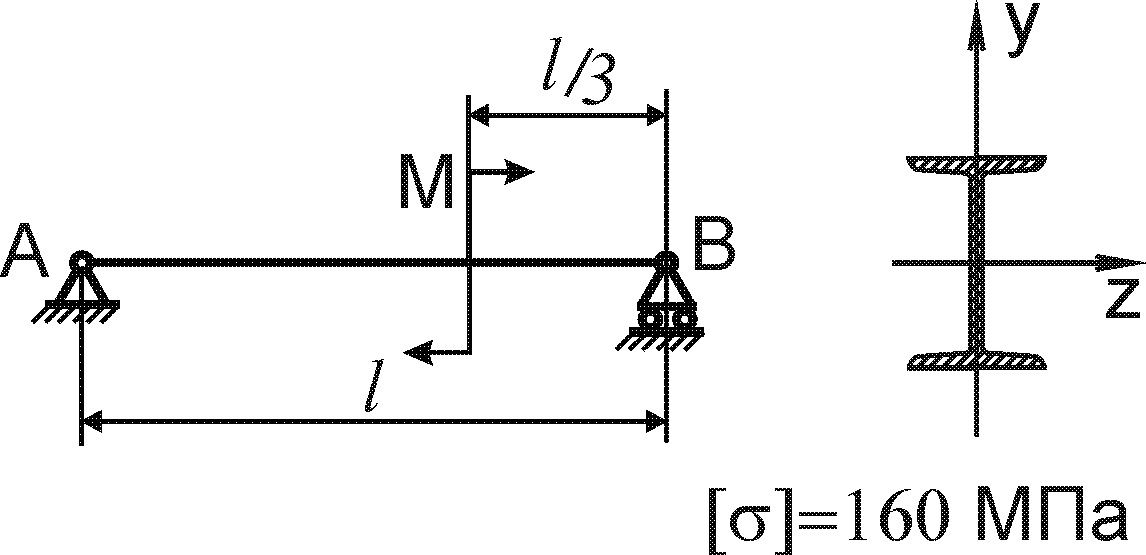
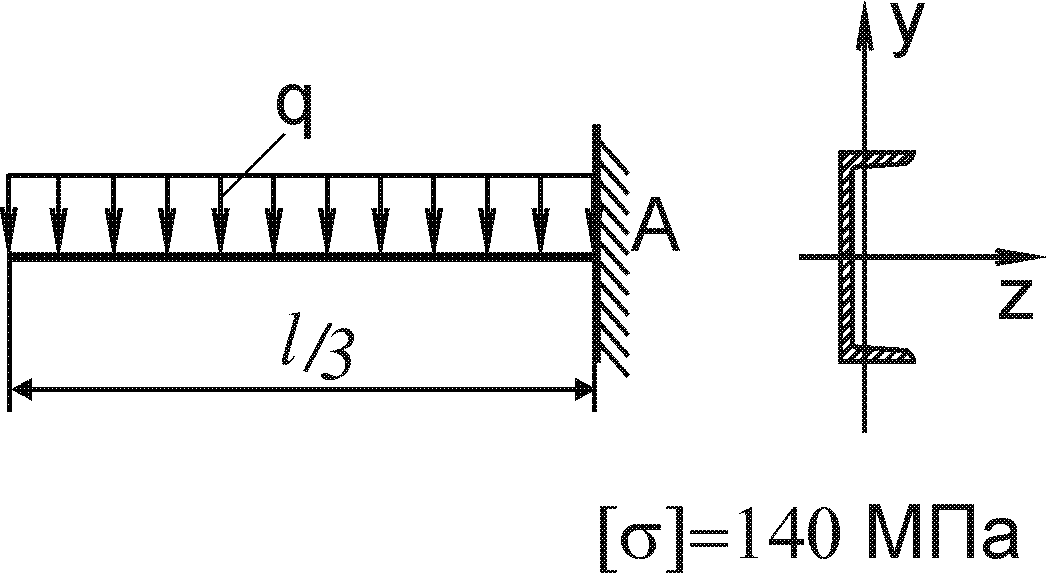
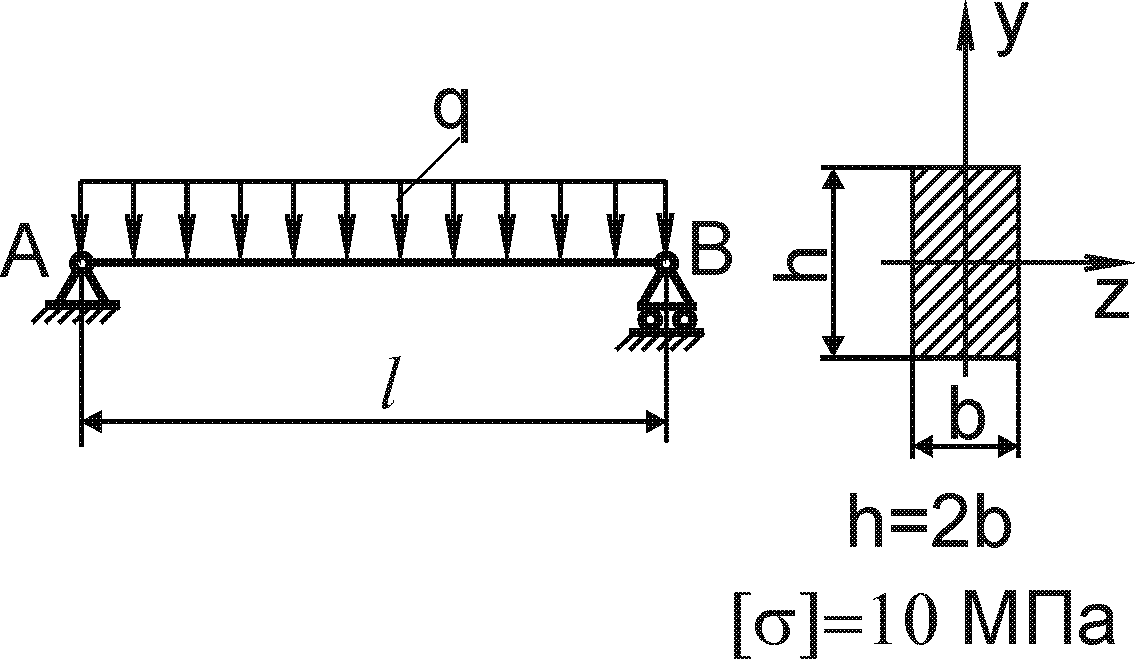
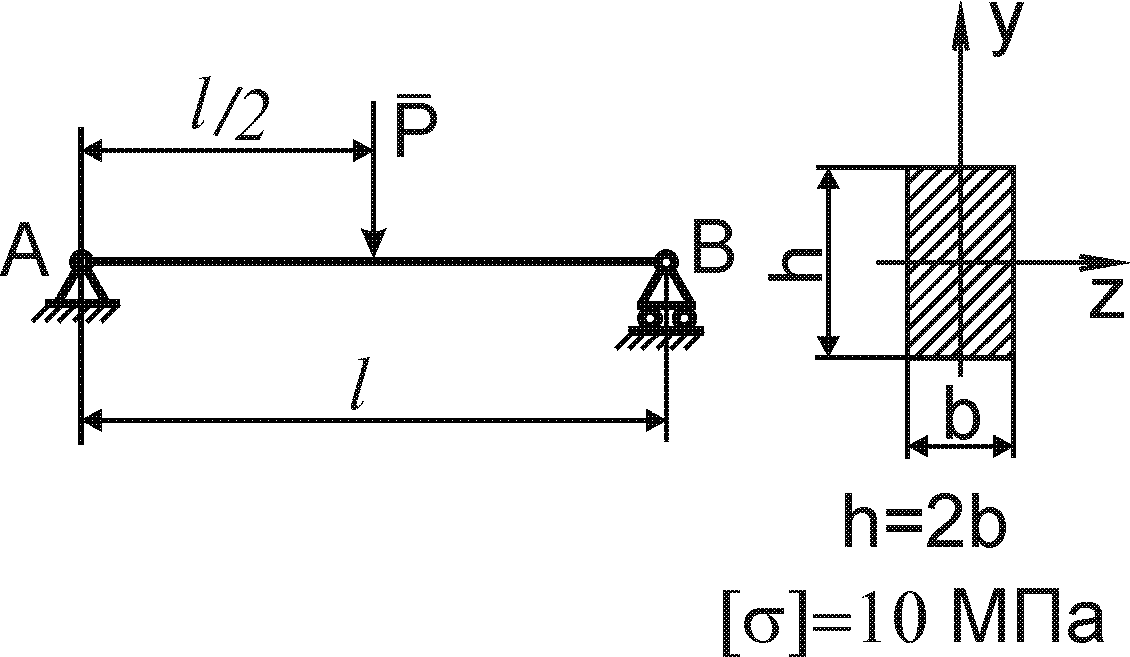
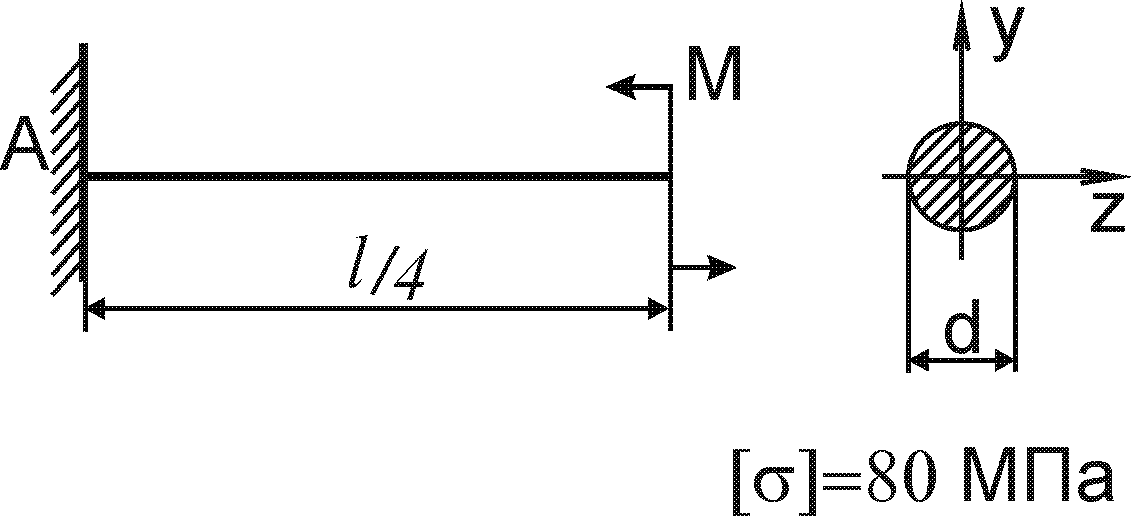
Завдання 8 - Згин

Для заданої балки побудувати епюри поперечних сил і згинаючих моментів та визначити геометричні параметри перерізу балки із умови міцності по нормальним напруженням (рис. 8.1).

Допустиме нормальне напруження матеріалу балок (сталь) [ ] = 120 Н/мм².

0	1
2	3
4	5
6	7
8	9

Рис. 8.1