6. Циркуляция вектора индукции магнитного поля

Циркуляцией вектора индукции магнитного поля (циркуляцией вектора ) называют криволинейный интеграл по произвольному контуру L скалярного произведения вектора индукции и вектора элемента этого контура , т. е.

, (25)

где  проекция на .

6.1. Теорема о циркуляции

Циркуляция по произвольному контуру L в вакууме равна произведению магнитной постоянной ₀ на алгебраическую сумму токов, охваченных этим контуром.

Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта, а ток противоположного направления  отрицательным (рис. 7, где I₁ > 0, I₃ > 0, I₂ < 0, I₄ < 0).

Рис.7.

Рассмотрим магнитное поле прямого проводника с током бесконечной длины (рис.8, ток направлен к нам). В качестве замкнутой поверхности используем окружность L радиуса r. Вектор индукции магнитного поля перпендикулярен радиус-вектору и совпадает по направлению с вектором элемента длины .

Рис. 8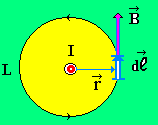

Согласно определению циркуляции вектора имеем

, (cos =1).

Применив формулу индукции прямого проводника с током бесконечной длины, последнее равенство перепишем в виде

. (26)

Теорема остается справедливой и для контура произвольной формы, который охватывает N проводников с током, т. е.

. (27)

Формулу (27) называют законом полного тока.

Если ток распределен по объему, где расположен контур L, то

.

Интеграл берется по произвольной поверхности S, натянутой на контур L.

Поэтому плотность тока под интегралом соответствует точке, где расположена площадка (направление обхода и вектор нормали связаны правилом правого винта). С учетом этого теорему о циркуляции запишем в виде

. (28)

Замечание 1: Магнитное поле называют вихревым, или соленоидальным, поскольку циркуляция вектора не равна нулю (в отличие от электростатического поля, которое является потенциальным).

Замечание 2: Поле вектора определяется всеми токами, а циркуляция вектора  только теми токами, которые охватывает данный контур.

6.2. Дифференциальная форма теоремы о циркуляции

Рассмотрим отношение циркуляции вектора к площадке S, натянутой на контур L. Ориентация этого контура связана с вектором нормали к плоскости контура правилом правого винта. В пределе при S  0, имеем

. (29)

Формулу (29) называют ротором поля .

Следовательно, этот предел представляет собой скалярную величину, равную проекции вектора на нормаль. Используя (29), формулу (28) представим в виде

(30)

или

, (31)

где  векторный дифференциальный оператор.

Следовательно,

. (32)

Ротор поля совпадает по направлению с вектором плотности тока в данной точке. Формула (32)  дифференциальная форма теоремы о циркуляции . Дифференциальная форма теоремы о циркуляции расширяет ее возможности для исследования и расчета сложных магнитных полей.