
- •Оглавление
- •1. Модели и системы 7
- •2. Технология моделирования 18
- •3. Непрерывные детерминированные модели 34
- •4. Модели массового обслуживания 64
- •5. Дискретные модели 94
- •Предисловие
- •Модели и системы
- •Физические и математические модели
- •Моделирование: системный подход
- •Общая модель функционирования
- •Технология моделирования Построение моделей
- •Содержательное описание системы
- •Концептуальное моделирование
- •Построение математических моделей
- •Истинность моделей
- •Непрерывные детерминированные модели Непрерывные модели динамических систем
- •Задачи анализа непрерывных систем
- •Основные определения
- •Построение фазовых портретов
- •Устойчивость точек равновесия
- •Линейные системы
- •Стационарное решение
- •Общее решение
- •Двумерные канонические системы
- •Простые канонические системы
- •Фазовые портреты простых канонических систем
- •Фазовый портрет простой линейной системы
- •Качественная эквивалентность
- •Непростые канонические системы
- •Нелинейные системы Глобальные и локальные фазовые портреты
- •Линеаризация нелинейных систем
- •Предельные циклы
- •Модели массового обслуживания Основные понятия. Терминология
- •Потоки событий
- •Пуассоновский поток событий
- •Распределение событий на малом интервале времени
- •Распределение событий в пуассоновском потоке
- •Распределение интервалов между событиями
- •Законы обслуживания
- •Марковские смо
- •Марковские цепи
- •Матрица перехода для пуассоновского потока заявок
- •Одноканальная смо с ожиданием
- •Многоканальная смо с ожиданием
- •Смо с отказами
- •Многоканальные смо с взаимопомощью
- •Замкнутые системы
- •Дискретные модели Конечные автоматы
- •Вероятностные автоматы
- •Сети Петри
- •Ординарные сети Петри
- •Библиографический список
Линейные системы
Система обыкновенных
дифференциальных уравнений
![]() ,
где
,
где
![]() ,
называется линейной системой размерности
n, если функция f(x)
- линейна. Линейную функцию f(x)
можно записать в матричной форме:
,
называется линейной системой размерности
n, если функция f(x)
- линейна. Линейную функцию f(x)
можно записать в матричной форме:
f(x) = Ax ,
где A - матрица коэффициентов, x- вектор переменных:
 ,
,
![]() .
.
Соответственно система обыкновенных дифференциальных уравнений принимает вид
![]() .
.
Таким образом, каждая
компонента вектора производных
![]() является линейной функцией переменных
является линейной функцией переменных
![]() .
При исследовании линейных систем не
возникает принципиальных трудностей,
ибо всегда можно получить решение
системы уравнений в аналитическом виде.
.
При исследовании линейных систем не
возникает принципиальных трудностей,
ибо всегда можно получить решение
системы уравнений в аналитическом виде.
Стационарное решение
Стационарное решение линейного дифференциального уравнения удовлетворяет системе линейных алгебраических уравнений Ax = 0.
Если матрица A
неособенная, т.е.
![]() ,
то система имеет единственное стационарное
решение, при котором все компоненты
вектора производных равны нулю:
,
то система имеет единственное стационарное
решение, при котором все компоненты
вектора производных равны нулю:
![]() .
В фазовом пространстве стационарное
движение (состояние) линейной системы
будет изображаться точкой, расположенной
в начале координат.
.
В фазовом пространстве стационарное
движение (состояние) линейной системы
будет изображаться точкой, расположенной
в начале координат.
Общее решение
Общее решение системы дифференциальных уравнений
![]()
определяется как
совокупность частных (фундаментальных)
решений вида
![]() .После
подстановки получаем линейную систему
алгебраических уравнений:
.После
подстановки получаем линейную систему
алгебраических уравнений:
x = Ax или (A - I)x = 0 , где I - единичная матрица.
Требование не тривиальности решений x(t) 0 приводит к характеристическому уравнению det(A - I) = 0 или в развернутом виде
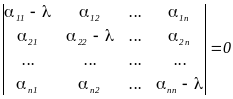 .
.
Таким образом, собственные значения матрицы A совпадают с характеристическими числами системы дифференциальных уравнений.
В общем случае i - комплексные величины i=i+ji . Тогда, если у матрицы A нет кратных собственных значений, аналитическое решение системы дифференциальных уравнений можно представить как сумму фундаментальных решений следующего вида:
если Im(i) = 0, то i-я компонента решения представляет собой экспоненту
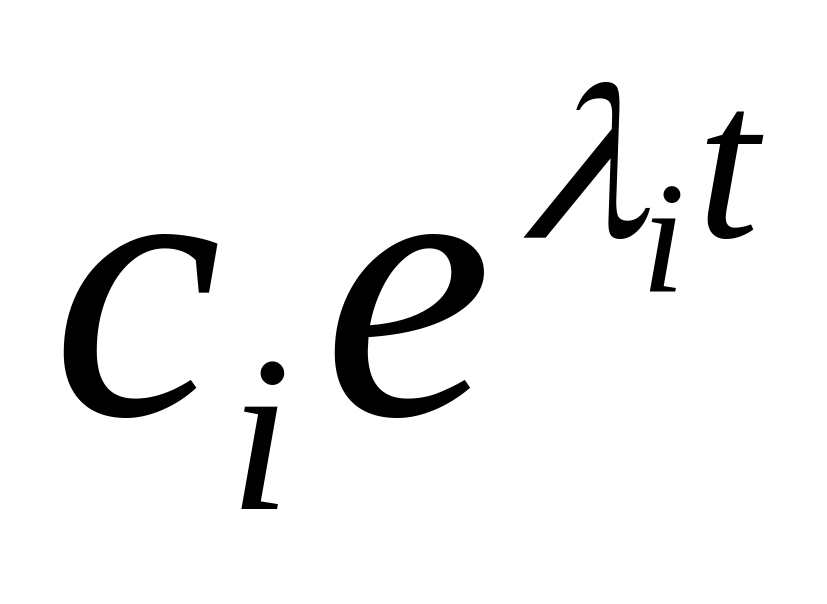 ,
затухающую при
,
затухающую при
 ,
а при
,
а при
 неограниченно
возрастающую;
неограниченно
возрастающую;если
 ,
то i-я
компонента решения представляет собой
экспоненциально взвешенную синусоиду
,
то i-я
компонента решения представляет собой
экспоненциально взвешенную синусоиду
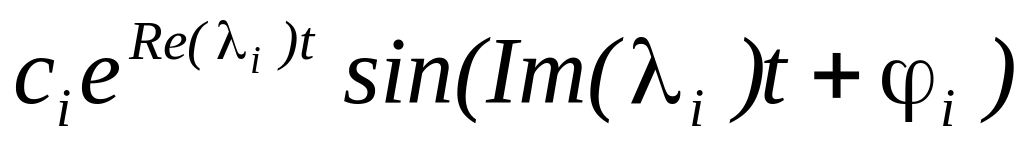 ,
затухающую при
,
затухающую при
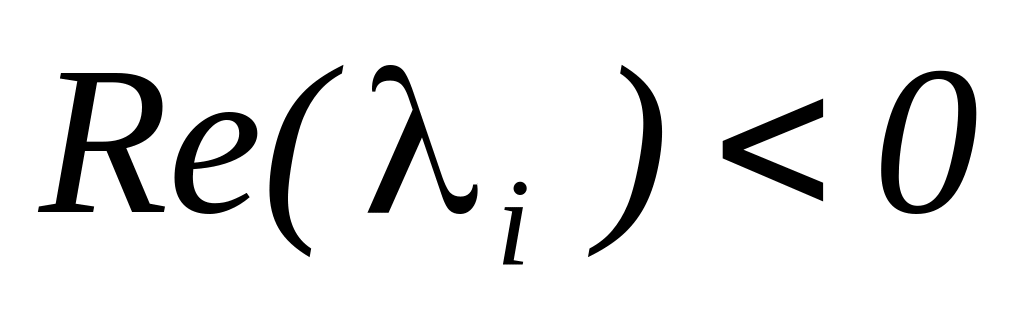 ,
с неограниченно возрастающей амплитудой
при
,
с неограниченно возрастающей амплитудой
при
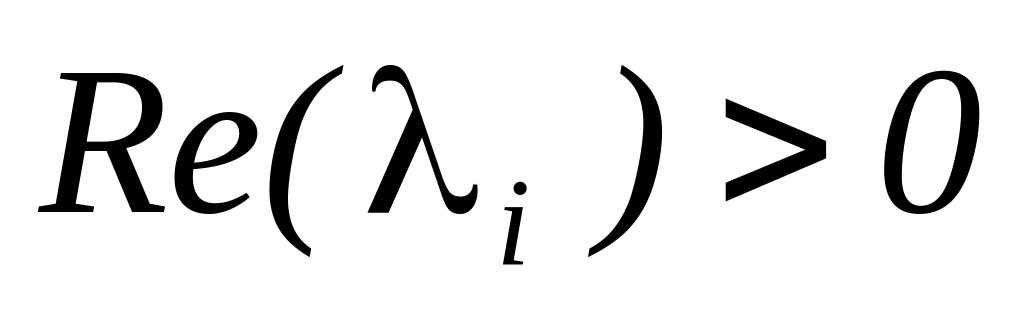 и с постоянной амплитудой при
и с постоянной амплитудой при
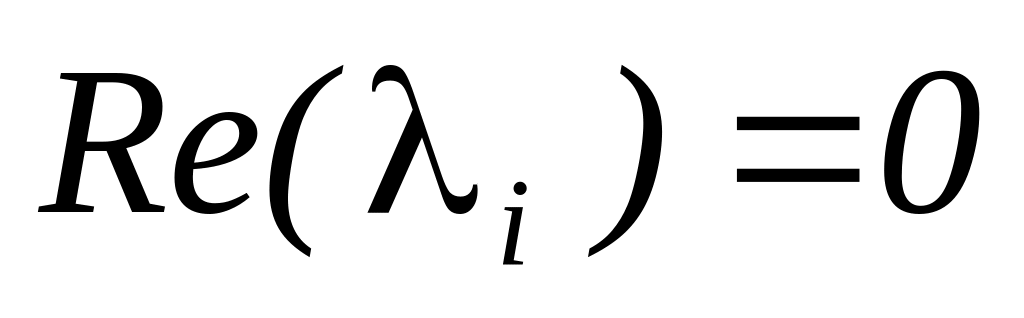 .
.
Двумерные канонические системы
Из линейной алгебры
известно, что любую двумерную линейную
систему
с помощью линейного преобразования
x=My
можно свести к канонической форме
![]() ,
где
,
где
![]() называется жордановой формой матрицы
A.
Жорданова матрица J
принадлежит к одному из четырех типов:
называется жордановой формой матрицы
A.
Жорданова матрица J
принадлежит к одному из четырех типов:
(a)![]() (b)
(b)![]() (c)
(c)![]() (d)
(d)![]() .
.
Для собственных значений матрицы A справедливо
![]()
или
![]() ,
,
где
![]() - след матрицы A,
а
- след матрицы A,
а
![]() - её определитель.
- её определитель.
Таким образом, собственными значениями являются
![]()
Соответствующая матрице A жорданова форма J зависит от вида собственных значений:
(а) > 0 , 1 2 - действительные различные;
(b,c) = 0 , 1 = 2 = 0 - действительные кратные;
(d) < 0 , 1,2 = j - комплексные сопряженные.
Простые канонические системы
Линейная система называется простой, если матрица A неособенная, т.е. detA 0 и A соответственно не имеет нулевых собственных значений. Тогда единственным решением уравнения Ax=0 является x=0 и система имеет единственную неподвижную точку в начале координат фазовой плоскости. Каноническая система, соответствующая простой линейной системе, также является простой, так как матрица A и соответствующая ей жорданова матрица J имеют одинаковые собственные значения.
