Билет №1.18. Определение скалярного произведения векторов. Основные свойства скалярного произведения векторов (с доказательством).
Скалярным
произведением векторов
и
называется
число, которое обозначается
и
равно произведению длин этих векторов
и косинуса угла между ними, т. е.
,где
–
угол
между векторами
и
.
В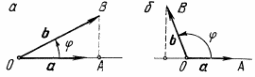
озьмем
в пространстве какую-либо
точку
и
построим такой отрезок
,
что
=
.
Обозначим
буквой
ось,
определяемую отрезком
.
Тогда при
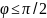(рис. а)
и при
/2
(рис. б)
получаем:
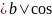ϕ
,
где
проекция ортогональная. Получим
.
Свойства скалярного произведения векторов: 1)
Коммутативность:
2)
Докажем
равенство
Равенство
3)
Дистрибутивность:
Поскольку
Равенство
следует из равенств
Из этих трёх свойств вытекает, что скалярное умножение двух векторов можно производить почленно. 4)
Необходимым
и достаточным условием перпендикулярности
(ортогональности) двух векторов
и
является
равенство нулю их скалярного
произведения:
Доказательство:
Если
векторы
и
перпендикулярны,
то
Обратно,
пусть векторы
и
удовлетворяют
равенству
.
Если хотя бы один из них нулевой, то
он не имеет определенного направления,
и его можно считать перпендикулярным
ко второму вектору. Если же оба вектора
a
и
b
ненулевые
и, следовательно,
5)
Скалярное
произведение вектора на себя, которое
обозначается
|
.
.
,
используя формулу
,
а также свойства проекций. Получим:
следует
из равенств
.
и
.
.
.
или
.
,
и равенство
справедливо.
,
то следует, что
и,
значит,
.
,
равно
квадрату длины этого вектора:
.
Билет №1.19. Выражение скалярного произведения векторов через координаты перемножаемых векторов (с доказательством). Критерий перпендикулярности двух векторов, заданных своими координатами. Выражение длины вектора через его координаты. Выражение косинуса угла между двумя векторами через их координаты.
Выражение скалярного умножения векторов через координаты перемножаемых векторов. Пусть в пространстве выбрана ДПСК с началом координат в точке . Составим таблицу скалярных произведений векторов :
,
.
С помощью соотношений (1) найдем скалярное произведение векторов и :
Таким
образом, скалярное произведение двух
векторов, заданных своими координатами
в прямоугольной системе координат
,
выражается формулой
|
(1)
.
.
Равенство
,
выражающее
необходимое и достаточное условие
перпендикулярности
двух векторов, теперь может быть записано
в виде
.
Исходя
из формул
и
,
получаем формулу для вычисления длины
вектора
.
Пусть заданы
координаты двух точек
и
.
Так как расстояние
между ними равно длине
вектора
,
то имеет место формула
.
Исходя из
формул
(12),
и
,
получаем выражение
для косинуса угла
между
векторами
и
:
.