8. Методы решения нелинейных уравнений: метод деления пополам. Метод половинного деления

Метод основан на одной из теорем математического анализа. Согласно [10], функция, непрерывная в замкнутом интервале и принимающая на концах этого интервала значения разных знаков, хотя бы один раз обращается в нуль внутри интервала.

Пусть функция f(x) непрерывна на отрезке . Процедура метода заключается в последовательном сокращении длины отрезка для локализации корня уравнения (3.1). Первоначально проверяются значения заданной функции на концах отрезка. В случае, если

,

один из концов отрезка является искомым корнем уравнения.

Пусть на концах отрезка значения функции имеют разные знаки, то есть имеет место соотношение

.

Вычисляется значение аргумента в середине отрезка, , и вычисляется значение функции в этой точке. Далее сравниваются знаки функции в точке и, например, в левой точке отрезка.

Если имеет место соотношение (рис. 3.1), то корень следует искать на отрезке . В противном случае - корень разыскивается на отрезке . В результате выполненной операции исходный отрезок сократился вдвое.

f(x₁)

f(x₃) f(x₂)

f(x₄)

x₀ x₃ x₂ x₁

x₄

f(x₀)

Рис. 3.1. Схема метода половинного деления

Далее, в зависимости от ситуации, отрезок вновь делится пополам,

и так далее.

Для прекращения вычислительной процедуры применяются различные критерии:

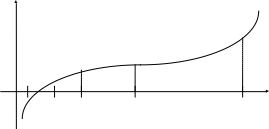
- если функция достаточно “пологая”, имеет смысл использовать условие (рис.3.2a)

;

- если функция “круто” меняет свое значение, целесообразно применять условие (рис.3.2b)

.

a b

Рис. 3.2. Частные случаи поиска корня нелинейного уравнения

В случае, если заранее неизвестен характер “поведения” функции, имеет смысл использовать одновременно оба условия для прекращения итерационного процесса.

9. Методы решения нелинейных уравнений: метод Ньютона, оценка погрешности и сходимость. Модификации метода Ньютона.

Для поиска корней уравнения (3.1) в окрестности решения выберем точку x и разложим функцию f(x) в ряд Тейлора возле этой точки:

.

Отсюда следует приближенное равенство

,

которое с учетом

позволяет получить выражение

,

приводящее к итерационному процессу следующего вида:

. (3.6)

Очевидно, что метод Ньютона можно рассматривать как вариант метода простых итераций, при условии .

Геометрическая иллюстрация итерационного процесса метода Ньютона приведена на рис. 3.4, из которого понятно, что каждое следующее приближение может быть определено из геометрических построений:

.

f(x)

f(x₀)

f(x₁)

f(x₂)



x₃ x₂ x₁ x₀ x

Рис. 3.4. Геометрический смысл процедуры метода Ньютона

Пример 3.2. Требуется определить корни уравнения .

Согласно рассмотренному методу Ньютона строится итерационная процедура

.

Поскольку

,

.

Таким образом, применение процедуры метода Ньютона к заданному уравнению приводит к вычислительному процессу

.

Для а=2 “точное” решение . Результаты расчетов приведены в табл. 3.2.

Таблица 3.2

Последовательность получения приближенного решения

уравнения методом Ньютона

Номер итерации	Приближения решения
1	2,0	-10,0
2	1,5	-5,1
3	1,416666667	-2,746078431
4	1,414215686	-1,737194874
5	1,414213562	-1,444238095
6	1,4142135624	-1,414525655
7	1,4142135624	-1,414213597
8	1,4142135624	-1,4142135624

Теорема 3.2. Пусть выполнены следующие предположения:

- - корень уравнения f(x) = 0;

- первая производная ;

- вторая производная непрерывна в А;

- константа , где .

Тогда, если , то метод Ньютона сходится, причем

. (3.7)

Доказательство.

Для оценки погрешности решения воспользуемся формулой Тейлора для функции f(x) возле точки :

.

В силу получаем соотношение

.

С другой стороны, согласно методу Ньютона,

.

Отсюда,

, (3.8)

то есть имеет место квадратичная сходимость.

Пусть . Из формулы (3.8) получаем

,

то есть оценка (3.7) выполнена для N=1. Допустим, что формула (3.7) верна для произвольного q. С учетом условия С<1, имеем

,

то есть , а следовательно определены

.

Из соотношения (3.8) получаем

Согласно (3.7)

.

С учетом этого, из предыдущего выражения следует:

Но это как раз и означает, что формула (3.7) справедлива при N = q+1.

В силу C<1 из выражения (3.7) следует сходимость метода Ньютона:

,

что и требовалось доказать.