Разрешимость системы алгебраических уравнений метода сеток

Для упрощения рассмотрим частный случай

.

Введем обзначения:

, , , .

Теперь задача (3.42) - (3.43) записывается в виде

(3.44)

Покажем, что соответствующая однородная система алгебраических уравнений

(3.45)

имеет только тривиальное решение.

Лемма 3.1. Пусть на отрезке [a, b] заданы некоторые числа , среди которых есть неравные между собой, и выполнены условия

, (3.46)

а также имеет место

.

Тогда среди чисел наибольшее положительное значение принимает либо , либо .

Пусть, напротив, наибольшее положительное значение достигается внутри отрезка [a, b] при некотором значении , причем либо , либо . Тогда в силу условия 1) получим

,

поскольку . Благодаря условию 2) имеем:

.

Пришли к противоречию с исходным предположением, что и доказывает лемму.

Лемма 3.2. Пусть на отрезке [a, b] заданы некоторые числа , среди которых есть неравные между собой, выполнены условия (3.46), а также имеет место

.

Тогда среди чисел наименьшее отрицательное значение принимает либо , либо .

Доказательство этого утверждения проводится аналогично предыдущему.

Теорема 3.7. Пусть выполнены условия (3.46). тогда однородная система алгебраических уравнений (3.45) имеет только тривиальное решение.

Доказательство. В соответствии с формулами (3.45) выполнены условия лемм 3.1 и 3.2 одновременно. В этом случае наибольшим и наименьшим значениями являются либо , либо . Но согласно формуле (3.45) . Но это означает, что и все остальные . Таким образом, система уравнений (3.45) имеет только тривиальное решение, и поэтому ее определитель отличен от нуля. Следовательно, исходная система линейных алгебраических уравнений (3.44) имеет единственное решение.

Оценка порядка аппроксимации

Разложим решение задачи (3.29) - (3.30) в ряды Тейлора вблизи точки :

,

Подставим эти выражения в разностный аналог (3.42) уравнения (3.29):

.

Первое слагаемое в этом выражении совпадает с исходным уравнением (3.29) и поэтому обращается в нуль. Погрешность аппроксимации

(3.47)

уравнения (3.29) разностным аналогом (3.42) имеет второй порядок.

26. Метод прогонки для решения сеточной задачи.

Запишем сеточную задачу (3.42) - (3.43) с учетом введенных ранее обозначений:

(3.48)

Введем соотношение

, (3.49)

использующее дополнительные переменные . С помощью (3.49) запишем выражение для :

.

Подставим два последних соотношения в уравнения (3.48):

,

которое будет выполняться при любом наборе значений , если имеют место равенства

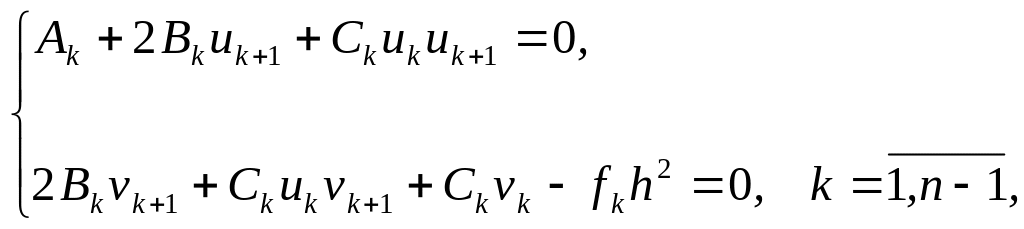
Это позволяет получить рекуррентные соотношения:

(3.50)

Прямой ход метода прогонки выполняется в следующей последовательности действий. Запишем выражение (3.49) для k = 0

и сравним с формулой

сеточной задачи (3.48).

Отсюда можно вычислить исходные значения

(3.51)

Далее используются формулы (3.50) для вычисления всех остальных величин .

Обратный ход метода прогонки. Формулу (3.49) при k = (n - 1), то есть , подставляем в последнее выражение системы (3.48):

,

,

.

Теперь, используя соотношение (3.49), можно определить все искомые величины .

Метод прогонки можно использовать в тех случаях, когда в приведенных формулах знаменатели дробей не обращаются в нули. В частности, можно избежать равенства нулю выражения ( ) в формулах (3.51) подбором соответствующего значения шага интегрирования h.

Покажем далее, что при условиях

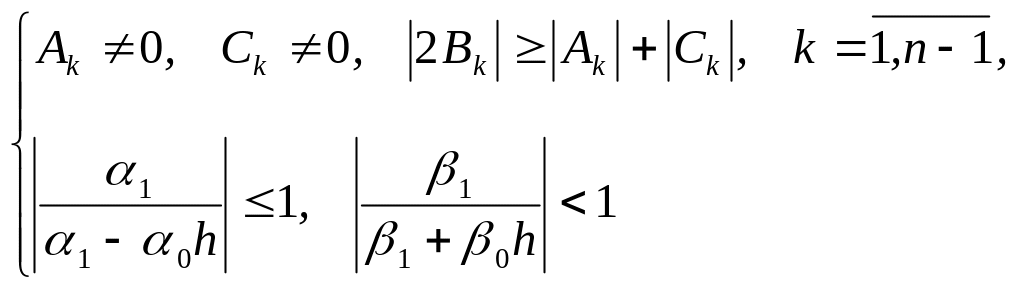(3.52)

знаменатели дробей и . Оценим значения переменных . Очевидно, что согласно условиям (3.52)

.

Предположим, что для произвольного значения k. Тогда с учетом (3.52)

,

то есть знаменатель отличен от нуля.

Более того, учитывая, что , получаем

.

Тем самым по индукции показано, что все .

Согласно условиям (3.52) .

Тогда и знаменатель

отличен от нуля.

1 Обозначение матрицы L принято по первой букве английского слова lower - “нижний”.

2Функция удовлетворяет условию Липшица на отрезке [a, b], если - константа