13.Гидродинамический и тепловой пограничные слои.

Для прилипания слоя жидкости характерны следующие особенности: частицы жидкости, непосредственно прилегающие к твердому телу, прилипают к его поверхности. Этот слой прилипшей жидкости рассматривать как бесконечно тонкий слой, и считается что скоростей жидкости у стенке =0. Это равенство скорости 0 выполняется, пока газ можно считать сплошной средой. По мере увеличения разрежения ослабляется взаимодействие газа со стенкой и разреженный газ вблизи стенки начинает проскальзывать. У поверхности твердого тела имеется тонкий слой неподвижной жидкости, для плотность теплового потока определяется по ур-ю Фурье: , где n- нормаль к поверхности тела. Если известно температурное поле, q_c , получаем ур-ие теплоотдачи . Коэф. теплоотдачи . Гидродин-ий пограничный слой. В области около пластины вследствие действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущенного потока (вдали от тела) –гидродин-ого пограничного слоя. Чем больше расстояние х от передней кромки пластины, тем толще пограничный слой, т. к. влияние вязкости по мере движения жидкости вдоль тела проникает в невозмущенный поток. Скорость в пограничном слое по мере увеличения у стремится к ω₀. При омывании тела поток жидкости как бы разделяется на две части: на пограничны и слой и на внешний поток. Во внешнем потоке преобладают силы инерции, в пограничном слое силы вязкости и инерционные силы соизмеримы. Уравнения движения , тоже самое только у на верху место х, и в конце. Уравнение сплошности (2). Т.к. толщена пограничного слоя очень маленькая величина, то поперег его давление не изменяется . Для пограничного слоя δ«l ур-ие движения принимает вид (1). Если Re<<1, а δ >> l нет разделения потока на две области, все пространство жидкости у тела охвачено действием сил вязкости. Если Re>>1, то δ << l , т. е. у поверхности тела образуется сравнительно тонкий слой подторможенной жидкости, для плоского стационарного течения вязкой жидкости в пограничном слое у плоской поверхности записать ур-ие 1 и 2.

14. Теория подобия. Метод масштабных преобразований.

Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны соответственно t₀ и . Размер тела l₀ задан. Температура поверхности тела равна t_c. Для определенности примем, что t_c>t₀. Будем полагать, что физические параметры жидкости. Теплота трения не учитывается. Рассматриваемый процесс является стационарным. Для простоты примем, что ось Oy нормальна к поверхности тела, а ось Ox направлена вдоль тела и вертикальна. При этом g_x=g, а проекции вектора сил тяжести на оси Oy и Oz будут равны нулю (g_y=g_z=0). Размер тела вдоль оси Oz намного больше l₀. В уравнениях и условиях однозначности можно различить три вида величин: – независимые переменные – это координаты x и y; – зависимые переменные – это ; зависимые переменные однозначно определяются значениями независимых переменных, если заданы величины, входящие в условия однозначности; – постоянные величины – это ; они задаются условиями однозначности и для определенной задачи являются постоянными, не зависящими от других переменных; от задачи к задаче они могут меняться; постоянными эти величины называют потому, что они не являются функцией независимых переменных. Обозначим безразмерные величины 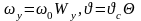. уравнения энергии: . Уравнение движения:

. Уравнения сплошности : Коэффициент теплоотдачи может быть определен по уравнению

.

15. Критерии подобия и критериальные уравнения. Число Нуссельта . Число Рейнольдса соотношение сил инерции и сил вязкости . Число Пекле . Число Грасгофа – хар-ет подъемную силу, возникающую в жидкости вследствие разности плотностей, т.е. свободное движение жидкости. . Число Архимеда Безразмерные величины θ,W_x, W_y, X, Y, Nu, Re, Pe, Gr переменные. Разделить на 3 гр.: - независимая; - зависимая; - постоянная. Nu = f₁(X_с, Y_с, Re, Pe, Gr); θ= f₂(X, Y, Re, Pe, Gr); W_x= f₃ -//-; W_y= f₄-//-. Число Эйлера – соотношение сил движения и сил инерции. , где р₀ какое-либо фиксированное значение давления, например давление на входе в канал. Число Ре можно представить как произведение 2-ух безразмер. переменных Ре=Rе . Число Прандтля . Число Прандтля показывает подобие полей тем-р и скоростей. Для жид. ч.Прандтля сильно зависит от тем-ры при увеличении тем-ры, ч. Прандтля уменьшается. Для газов ч. П. практически не зависит от тем-ры и давления, а опр-ся атомностью газов. Ур-ие энергии , ур-ие движения . Nu = F₁(X_с, Y_с, Re, Pe, Gr); θ= F₂(X, Y, Re, Pe, Gr); W_x= f₃ -//-; W_y= f₄-//-.