5. Условия однозначности для процессов теплопроводности.

Частные особенности, которые совместно с диф-ым уравнением дают полное математическое описание конкретного процесса теплопроводности, наз. условиями однозначности или краевыми условиями. Условия однозначности включают в себя: геометрические условия, характеризующие форму и размеры тела, в которых протекает процесс; физические условия, характеризующие физические свойства среды и тела; временные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени; граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.

Г еометрическими условиями задаются несколькими способами. а) Граничные условия первого рода. При этом задается распределение температуры на поверхности тела для каждого момента времени. . б) Граничные условия второго рода. При этом задаются значения теплового потока для каждой точки поверхности тела и любого момента времени. . в) Граничные условия третьего рода. При этом задаются окружающей среды tж и закон теплообмена между поверхностью тела и окружающей средой. Урав-е теплоотдачи где α – коэффициент пропорциональности, наз. коэф-ом теплоотдачи, Вт/(м2·К). Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи, должно равняться теплоте, подводимой к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела, т.е.

6. Стационарная теплопроводность однослойной и многослойной стенки при граничных условиях 1 рода. При установившемся, или стационарном, тепловом режиме температура тела во времени остается постоянной, т.е. ∂t /∂τ = 0При этом дифференциальное уравнение теплопроводности иметь вид или . а) Граничные условия первого род. Условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Диф-ое уравнение теплопроводности для рассматриваемого случая запишется в виде Граничные условия в рассматриваемой задаче зададим следующим образом: при х=0 t=t_c1 ; при х=δ t=t_c2 Путем математических преобразований получим: t=C₁х+C₂ при постоянном коэффициенте теплопроводности тем-ра в стенке изменяется по линейному закону. Постоянные С ₁ и С ₂ опр-ся из граничных условий: при х=0 t=t_c1 и С₂= t_c1 ; при х=δ t=t_c2 и С₁= -(t_c1- t_c2)/δ

Закон распределения температуры в рассматриваемой плоской стенке . Где t_c1 тем-ра наружной стенки; t_c2 тем-ра внутренней стенки; δ толщина стенки; x расстояние от наружной поверхности стенки, для которого определяется тем-ра. Обозначим текущий температурный напор или избыточная тем-ра; полный температурный напор или наибольшая избыточная тем-ра . Обозначив – безразмерный температурный напор или безразмерная избыточная тем-ра; безразмерная координата; получим . Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, воспользуемся законом Фурье Отношение λ/δ, Вт/( м ²·К), называется тепловой проводимостью стенки, а обратная величина δ/λ, (м 2 ·К)/Вт тепловым или термическим сопротивлением стенки. Общее количество теплоты Qτ , которое передается через поверхность стенки величиной F за промежуток времени τ: ур-ие тем-ого поля Из этого ур-ия следует, что при прочих равных условиях тем-ра в стенке убывает тем быстрее,чем больше плотность теплового потока. Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и тем-ра на соприкасающихся поверхностях двух слоев одинакова.можно составить систему уравнений

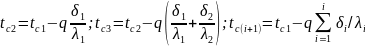. Определив температурные напоры в каждом слое и сложив правые и левые части полученных ур-ие, плотность теплового потока . Величина равна сумме термических сопротивлений всех n слоев, называется полным термическим сопротивлением теплопроводности многослойной стенки. Тем-ы на границах соприкосновения двух соседних слоев равны для многослойной стенки в целом температурная кривая представляет ломаную линию.