Определение моментов инерции тел с помощью трифиллярного подвеса и проверка теоремы Штейнера

Лабораторная работа №3

Алсагаров А.А., Шагдаров В.Б.

Редактор Т.Ю.Артюнина

Подготовлено в печать 98 г. Формат 6080 1/16

Усл.п.л. 0,46; уч.-изд.л. 0,4; Тираж 50 экз.

___________________________________________________

РИО ВСГТУ, Улан-Удэ, Ключевская, 40а

Отпечатано на ротапринте ВСГТУ, Улан-Удэ,

Ключевская, 42

 Восточно-Сибирский государственный

технологический университет

Министерство образования РФ

ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

Механика

Лабораторная работа №3.

Определение моментов инерции тел с помощью трифиллярного подвеса и проверка теоремы штейнера.

Составили: Алсагаров А.А.

Шагдаров В.Б.

Улан-Удэ 1999

4. Почему натяжение нитей трифиллярного подвеса должно быть одинаковым?

5. Какой закон заложен в основу вывода расчетной формулы для величин моментов инерции? При каких упрощающих предположениях выведена эта формула?

6. Объясните теорему Штейнера.

7. Выведите формулу погрешности для определения экспериментального значения момента инерции.

Лабораторная работа № 3.

Определение моментов инерции тел с помощью трифиллярного подвеса и проверка теоремы штейнера

Цель работы: определение моментов инерции некоторых тел методом крутильных колебаний с помощью трифиллярного подвеса и проверка теоремы Штейнера.

Принадлежности: трифиллярный подвес, секундомер, линейка, исследуемые тела (два диска- груза).

Одним из методов измерения моментов инерции твердых тел является метод трифиллярного подвеса, совершающего крутильные колебания. Поэтому, вначале определим, какие колебания называются крутильными, затем ознакомимся с устройством трифиллярного подвеса.

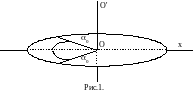
Гармонические крутильные колебания

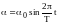
Гармоническими крутильными колебаниями тела называются периодические движения относительно оси, проходящей через центр масс этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или косинуса (рис. 1)

(1)

где ₀ - амплитуда колебаний, Т - период колебаний.

Устройство трифиллярного подвеса (рис. 2)

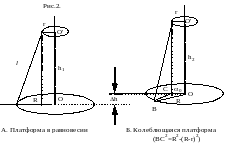
Трифиллярный подвес состоит из подвижного диска платформы Р ( в дальнейшем просто платформа) массой М, радиуса R, подвешенного на трех симметрично расположенных нитях.

Наверху эти нити симметрично закреплены по краям диска Р' меньшего радиуса r.

При повороте верхнего диска P' на небольшой угол  вокруг вертикальной оси OO' все три нити принимают наклонное положение. Центр тяжести системы несколько приподнимается по оси вращения OO' (рис. 3. А,Б).

Период крутильных колебаний и момент инерции платформы

Пусть при вращении платформа поднимется на высоту h=h₁-h₂, тогда приращение ее потенциальной энергии равно

E_n = Mqh,

где q - ускорение свободного падения.

При вращении платформы в обратную сторону потенциальная энергия переходит в кинетическую энергию вращательного движения

,

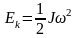где J - момент инерции платформы;  - ее угловая скорость.

В момент прохождения положения равновесия кинетическая энергия максимальна. Если пренебречь трением, то на основании

3.1. Для проверки теоремы Штейнера разместить два груза симметрично на расстоянии, а от оси вращения платформы (в опыте используется два груза для сохранения горизонтального положения платформы). Подобное распределение масс в системе, как было указано выше, приведет к увеличению ее момента инерции, хотя общая масса системы при этом остается постоянной.

3.2. Выполнить пункт 1.1. и определить период колебаний Т₂ платформы с разнесенными грузами.

3.3. Определить момент инерции этой системы по формуле

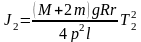
Так как J₂=J_пл+2J'_гр, то момент инерции груза J'_гр, центр масс которого находится на расстоянии а от оси вращения, равен

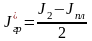
3.4. Вычислить момент инерции груза по теореме Штейнера

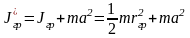
и сравнить с экспериментальным значениям.

Экспериментальное значение момента инерции	Теоретическое значение момента инерции

4. Вычислить погрешности.

5. Сделать выводы.