Элементы неравновесной термодинамики. Движущие силы процессов при отклонении от равновесия.

Для определенности считаем систему в целом изолированной и в ней будем рассматривать состояния близкие к равновесным. Т. е. будем говорить о слабонеравновесных изолированных системах. Пусть _k – совокупность макроскопических (экстенсивных) параметров, характеризующих отклонение от равновесного состояния, для которого все _k = 0 . Например, если в равновесном состоянии число частиц в системе равно N_p , то в качестве ₁ можно взять отклонение N = N – N_p от состояния равновесия ₁ = N. При равновесии, согласно 2-му началу термодинамики, энтропия имеет максимум, т. е. S/_k = 0 при всех k . Кроме того состояние равновесия системы устойчиво ко всем флуктуациям параметров вблизи точки равновесия, приводящим к уменьшению энтропии S < 0. Далее в системе происходят необратимые процессы, сопровождаемые ростом энтропии и в результате снова достигается равновесие: S = S_max . В частности, при флуктуации температуры условие устойчивости приводит к необходимости выполнения неравенства C_v > 0 .

В случае функции одного переменного о поведении данной функции в окрестности некоторой точки хорошее представление дает ее аппроксимация линейной функцией – дифференциалом. Однако в точке экстремума производная обращается в нуль и нетривиальные свойства функции определяются первым ненулевым слагаемым ее разложения в ряд Тейлора в окрестности экстремума. Для слабонеравновесной теории будет достаточно сохранения квадратичного слагаемого

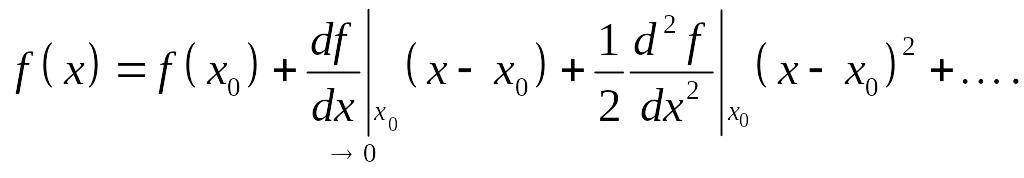
В термодинамике подобный вариант для одной независимой переменной имеет право на существование, однако значительно интереснее и важнее случай нескольких переменных. Фактически теорию полностью иллюстрирует случай 2-х переменных. Большее число переменных приводит только к некоторому усложнению записи и анализа конкретных ситуаций. Поэтому ограничимся случаем k = 2 и обозначим независимые переменные  и  (₁ =  , ₂ = ).

Разложим энтропию в ряд Тейлора в окрестности равновесного состояния

где параметры _ij определены при равновесных условиях:

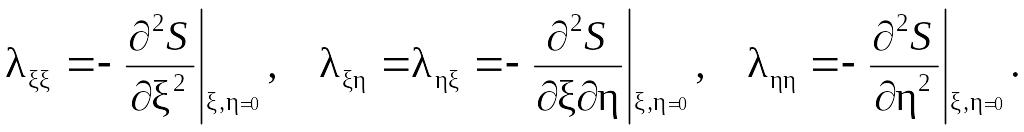
Слагаемые третьего порядка ряда Тейлора отброшены, а знаки минус введены с целью сделать параметры _ и _ положительными. Определим соответствующие переменным  и  «обобщенные силы» (они так называются, поскольку вызывают релаксацию к равновесию)

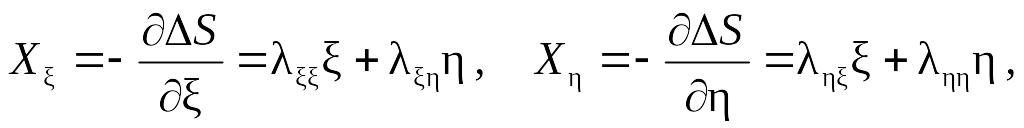S = S(,) – S(0,0) . (1)

Отметим, что силы X_ и X_ при наших ограничениях связаны с координатами  и  линейно. Введем соответствующие координатам  и  потоки (экстенсивных переменных)

J_ = d/dt , J_ = d/dt .

Величины этих потоков определяются не только свойствами данной системы, но и отклонениями величин  и  от равновесия, т.е. J_(,) , причем J_(0,0) = 0 – в состоянии равновесия. В отличие от равновесной термодинамики в теории появляется время. Масштаб этого времени значительно превышает характерное время молекулярного взаимодействия.

22. Связь потоков и сил. Соотношения Онзагера.

Связь потоков и сил. Соотношения Онзагера.

При малых  и  можно ограничиться в формулах для потоков J_(,) линейными по  и  слагаемыми, или, в силу (1), линейными по X_ и X_ , т. е.

J_ = L_X_ + L_X_ = l_ + l_ , (2)

где

l_ = L__ + L__ , l_ = L__ + L__ , l_ = L__ + L__ .

Для функций J_ достаточно в выписанных формулах заменить    .

Онзагер обосновал симметричность матрицы коэффициентов L_ = L_ , которая имеет место при любом числе параметров _k . Физический смысл условия L_ = L_ состоит в том, что поток J_ , вызываемый силой X_ такой же как поток J_ вызываемый силой X_ . Теория Онзагера описывает линейную релаксацию значений экстенсивных переменных к их равновесным значениям.

Выражение (2) ограничивает теорию рассмотрением только линейных эффектов в неравновесной термодинамике. Отметим, что именно линейные эффекты являются основными в задачах диффузии, теплопроводности, вязкого трения и т. п., в которых в качестве исходных положений используются известные из экспериментов соотношения, выражающие прямую пропорциональность величин стационарных потоков градиентам соответствующих параметров. В частности закон Фурье (1822 г.) для теплопроводности, Фика (1855 г.) для диффузии, Ома (1826 г.) для электрической проводимости.

Одна из задач теории и практики рассматриваемых слабонеравновесных необратимых процессов состоит в установлении универсальных связей между кинетическими коэффициентами, характеризующими разные процессы переноса в данной системе. Число независимых соотношений в матрице L в силу соотношений взаимности Онзагера

L_ij = L_ji , i , j = 1 , 2 , …, n ;

Рис. 1

равно 1 + 2 + 3 + … + n = n(n + 1)/2 согласно формуле арифметической прогрессии.

23. Скорость возрастания энтропии. Внешнее и внутреннее изменение энтропии открытой системы.