Изотермический процесс.

T = const , q_T = Ts , C_T   , l^v_T = q_T – u , располагаемая работа l^p_T = q_T – h . Для идеального газа pv = const и u = u(T)  u = 0  l^v_T = q_T = Ts .

Работа расширения

11. Изобарно-изотермный процесс идеального газа, располагаемая работа, работа расширения (сжатия), теплота процесса, теплота конденсации, теплота испарения.

Изобарно-изотермный процесс.

Изобарно-изотермные процессы реализуются при испарении и конденсации насыщенного пара. При наличии двух фаз равновесие между ними реализуется при равенстве соответствующих интенсивных параметров (p – механическое равновесие; T – тепловое). При этом T_s – называется температурой насыщения, а p_s – давлением насыщения. Удельная (на единицу массы) теплота фазового перехода жидкость – насыщенный пар называется удельной теплотой парообразования или испарения – r , [r] = Кдж/кг

r = h^ – h^ = T_s(s^ – s^) > 0 .

Рис. 6. отсутствует

Первое равенство следствие изобарности процесса, второе – его изотермности. В обратном процессе – конденсации пара эту величину называют удельной теплотой конденсации. Теперь r = h^ – h^ < 0 . Основные характеристики: T_s , p_s и x – степень сухости влажного пара. Отметим, что при T ≥ T_к различие между газом и жидкостью отсутствует.

12. Политропный процесс идеального газа, располагаемая работа, работа расширения (сжатия), теплота процесса. Дифференциальные уравнения идеального газа. Их интегральный вид.

Политропный процесс.

Обобщенный процесс для идеального газа, включающий ряд термодинамических процессов как частные случаи, подчиняющийся уравнению

pvⁿ = const ,

называют политропическим процессом, n – показатель политропы.

n = 0 – изобарный процесс, n   – изохорный процесс (v = const),

(pvⁿ = pv₀ⁿ  p^1/nv = p^1/nv₀  v  v₀ = const при n  )

n =  – адиабатный процесс, n = 1 – изотермический процесс.

Политропный процесс характеризуется постоянной теплоемкостью C_n . Это второе (независимое) определение политропного процесса. Для идеального газа можно получить соотношение (получим на семинаре)

(2)

Для теплового эффекта по второму определению политропного процесса, имеем

q_n = C_nT .

Соответственно для изменения внутренней энергии и работы имеем

u = C_vT , l_n = q_n – u = (C_n – C_v)T = ,

где учли формулу (2), уравнение Менделеева-Клапейрона и равенство T = T₂ – T₁ . В случае адиабаты C_n = 0 , имеем n =  .

Уравнения для работы получаются из соответствующих уравнений для адиабатного процесса заменой   n .

13. Первый закон термодинамики (в общем виде) для потока вещества.

Первый закон термодинамики для потока вещества.

Пусть идеальный, нетеплопроводящий газ ( = 0 ,  = 0 ,  – коэффициент динамической вязкости,  – коэффициент теплопроводности) движется в однородном поле тяжести. В каждом сечении S трубки тока (см. рис. 1) выполняется локальное термодинамическое равновесие. Имеем следующий закон сохранения вещества при стационарном течении (уравнение расхода)

Рис. 1. (отсутствует)

j = SW = SW/v = const .

За малое время t через любое сечение проходит M = jt количество вещества. Далее находим изменение различных видов энергии в трубке (разность между выходящим и входящим потоком энергии на торцах трубки тока)

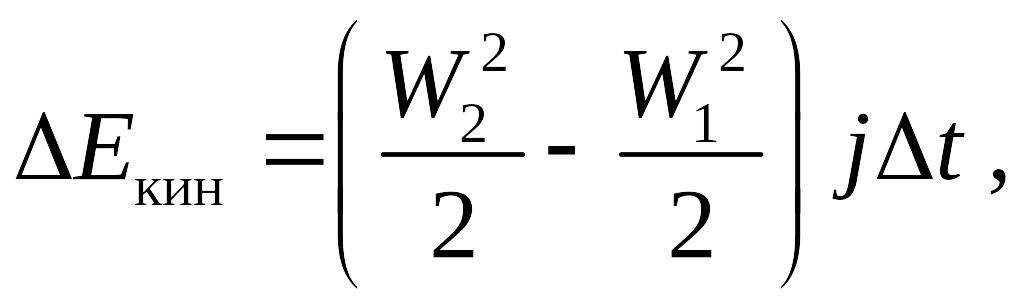
E_пот = g(z₂ – z₁)jt ,

E_внут = (u₂ – u₁)jt ,

–E_внеш = W_внеш = F₁l₁– F₂l₂ = (p₁S₁)(W₁t) – (p₂S₂)(W₂t) = –(p₂v₂ – p₁v₁)jt .

Величина W_внеш – работа внешних сил давления над газом за промежуток времени t , заставляющих его двигаться. В идеальной жидкости (газе) через боковую поверхность трубки обмена механической энергии нет. Из баланса энергии для вещества между сечениями S₁ и S₂ находим выражение для подведенной теплоты qjt после сокращения на величину jt :

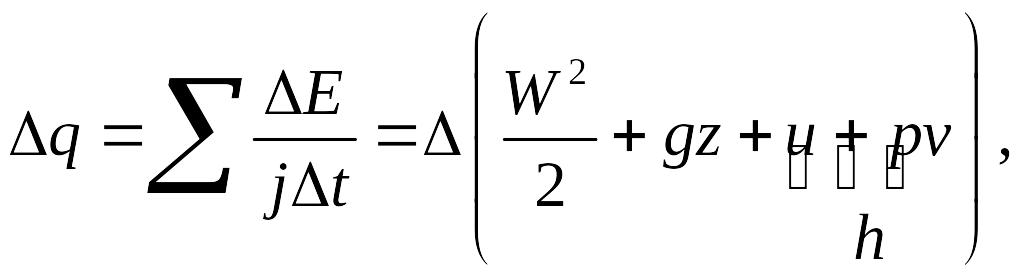
где учтено равенство h = u + pv . В дифференциальной форме имеем

dq = WdW + gdz + dh . (1)

Соотношение (1) показывает, почему в энергетическом балансе даже при медленных течениях (пренебрежении слагаемым WdW) и отсутствии перепада высоты dz = 0 используется энтальпия (dq = dh), а не внутренняя энергия, как это реализуется при отсутствии потоков (например, в периодических процессах).

Отметим, что при движении работа сил давления не равна pdv . Давление меняется от точки к точке и это существенно. При наличии потока вещества процесс не будет квазистатическим (обратимым) так как равновесие нарушено. Отметим также, что при выводе уравнения (1) не учтены возможные работы технических устройств и сил трения (идеальная жидкость). В ТТ уравнение (1) дополняют соответствующими слагаемыми: l_техн – технической работой и работой сил трения l_трен и используют следующее уравнение

q = WdW + gdz + du + d(pv) + l_техн + l_трен .

14. Первый закон термодинамики для адиабатного потока вещества при отсутствии технической работы. Уравнение Бернулли.