3 Вектора , и наз компланарными, если они лежат в одной плоскости. Сумма 2х векторов и -вектор , начало кот совпадает с началом вектора , а конец – с концом .

Если и имеют общее начало, то сумма совпадает с диагональю параллелограмма, построенного на этих векторах.

С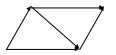 в-ва суммы:

Разностью 2х векторов и наз , такой, что . Обозн

Произведение вектора , отличного от , на число , наз вектор , , удовлетворяющ. след. условиям:

и коллинеарны

если , то векторы одинаково направлены, если -противоположно направлены.

Св-ва:

Два вектора коллинеарны тогда и только тогда, когда , для нек-рого действительного числа .

Проекция вектора на плоскость

П усть в пр-ве задана нек-рая ось и нек-рый вектор АВ. Проекцией вектора АВ на ось наз величина вектора ,взятая со знаком «+», если направление совпадает с направлением оси и со знаком «-«- если направлен противоположно.

Св-ва:

Координаты вектора.

Пусть в пр-ве задана прямоуг. с-ма координат и произвольный вектор АВ.

Пусть

Проекции вектора АВ наз-ют координатами

Т. Для любых двух точек А и В координаты АВ определяются по ф-ле

Длина вектора.

Пусть произвольный вектор . Построим равный ему вектор, начало к-рого совпадает с началом координат. Проведем через конец вектора плоскости  осям координат. Вместе с координатными осями и координатными плоскостями образуют прямоугольный параллелепипед, диагональю к-рого служит отрезок ОА.

Вопрос №11.Скалярное, векторное и смешанное произведение векторов.

Р азложение вектора по базисным векторам.

Пусть задана прямоуг. с-ма координат. Введем в рассмотрение единичные векторы, коорд. осей . -базисные вектора с-мы координат или орты. -произвольный вектор пр-ва. Отложим из начала координат вектор . По св-вам координат . Пусть числу на оси Ох соотв-ет точка , на . Тогда , ,

- ф-ла разложения по базисным векторам.

Пр. (1;2;3)

(1;0;0)+2(0;1;0)+3(0;0;1)=

Скалярное произведение векторов.

О.Скалярное произведение двух векторов и – число, равное произведению их модулей на угла между ними.

Св-ва:

тогда и только тогда, когда

угла между векторами вычисляется по ф-ле:

Т. Если векторы имеют координаты ; , тогда

Правые и левые с-мы координат.

Три некомпланарных вектора в указанном порядке наз-ют тройкой векторов.

П усть отложены из одной точки, будем смотреть из конца вектора на плоскость, содержащую и . Если кратчайший поворот от к осуществляется против часовой стрелки, то тройка векторов наз правой тройкой, если по часовой-то левой.

Векторное произведение векторов.

О. Векторным произведением на наз , к-рый удовлетворяет след. условиям:

каждому из векторов и

тройка векторов

Св-ва:

и -коллинеарны только тогда, когда =0

площадь параллелограмма, построенного на векторах и = модулю векторного произведения

Т. Пусть , , тогда

Разложим и по базисным векторам

=

x	i	j	k
i
j
k

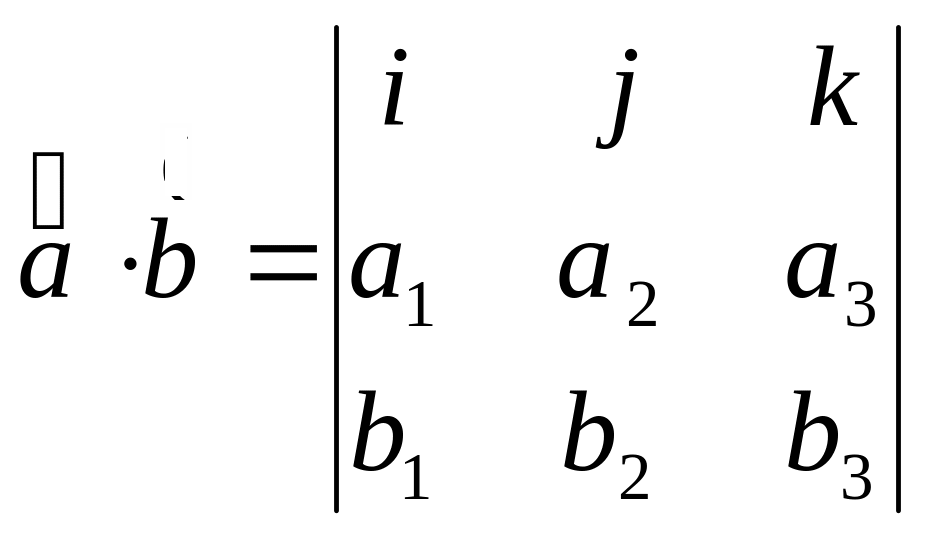
Смешанное произведение

Пусть даны 3 вектора . Умножим векторно, а полученный р-т скалярно на . В р-те получим число , называемое смешанным произведением векторов .

Смешанное произведение 3-х некомпланарных векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если тройка правая и со знаком «-« - если правая.

Следствие. компланарны только тогда, когда их смешанное произведение =0.

Т. Пусть , , , тогда

Вопрос №12. Плоскость в пространстве.

Ур-ние плоскости по точке и норм. вектору.

П усть дана точка и плоскости. Пусть -произвольная точка плоскости. Рассм. вектор

(1)  (2)

(1)-ур-ние по точке и нормальному вектору, (2)-общее ур-ние плоскости.

Частные случаи:1)если , то плоскость проходит через начало координат

2)если , тогда оси . След-но плоскость параллельна оси

3) плоскость проходит через ось

4) плоскость параллельна плоскости

5) плоскость определяет координатную плоскость

Ур-ние плоскости, проходящей через 3 данные точки

Р ассм. 3 точки, не лежащие на одной прямой , , . Рассм. произвольную точку , лежащую в этой плоскости. Рассм. .

, ,

т.к. компланарны, то их смешанное произведение =0, т.е. - ур-ние плоскости по 3 точкам.

Взаимное расположение двух плоскостей.

Пусть даны 2 плоскости 1-ая плоскость имеет , . Если плоскости параллельны, то и коллинеарны. Поэтому – условие параллельности плоскостей. –условие совпадения плоскостей. Если условие параллельности не выполняется, то плоскости пересекаются. В частности  плоскостей равносильна  их нормальных векторов.

- условие перпендикулярности.

Угол между двумя плоскостями.

-угол между их нормальными векторами, т.е.

Вопрос №13. Прямая в пр-ве.Векторно-параметрическое ур прямой.

Направляющим вектором прямой наз любой вектор, лежащий на прямой или параллельной ей.

Составим ур прямой, проходящ. через  . Отложим из вектор . Пусть -произвольная точка прямой - её радиус вектор. Тогда .

- векторно-параметрическое ур-ние прямой.

Параметрическое ур-ние прямой

В векторно-параметрическое ур-ние подставим координату векторов. Тогда

-параметрическое ур-ние прямой.

Выразим в каждом из ур-ний параметр .

- каноническое ур-ние.

Ур-ние прямой, проходящей через две данные точки.

Пусть прямая прох через точки и . В кач-ве направляющего вектора данной прямой можно выразить вектор .Будем составлять ур прямой, проход. через  . Получим

-ур-ние прямой, прох через две данные точки.

Угол между двумя прямыми. Рассм. 2 прямые с направляющими векторами и . Угол между прямыми = углу между их направляющими векторами, т.е.

- условие перпендикулярности.

Прямые  если их направляющие вектор коллинеарные. .

Взаимное расположение прямых в пр-ве.

Пусть даны две прямые и . Очевидно, что прямые лежат в одной плоскости, если вектора и – компланарны, т.е. определитель будет =0.

Если в определителе первые две строки пропорциональны, то прямые . Если все 3 строки пропорц., то прямые совпадают. Если определитель =0 и первые 2 строки не пропорциональны, то прямые пересекаются. Если данный опред. отличен от нуля, то прямые скрещиваются.

Вопрос №14.Прямая как пересечение двух плоскостей.

Пусть даны 2 плоскости и (*). Если плоскости не явл. параллельными, то нарушается условие . Пусть например . Найдем ур-ние прямой, по к-рой пересекаются плоскости. В кач-ве направляющего вектора можно взять вектор . Подставим в с-му (*) и найдем

По предположению , т.е. опред. матрицы с-мы отличен от 0. След-но с-ма имеет единственное решение ( ). Тогда искомая точка имеет координаты ( ; ), а ур-ние прямой примет вид

Взаимное расположение прямой и плоскости в пространстве.

Пусть задана плоскость и прямая . Чтобы найти общие точки необх реш с-му

если , то с-ма имеет единственное решение. В этом случае прямая и плоскость пересекаются в единственной точке , где

если , то решений нет, т.е. прямая и плоскость параллельны.

и . С-ма имеет бесконечное множ-во решений, т.е. прямая принадлежит плоскости.

Угол между прямой и плоскостью.

Найдем угол между прямой и плоскостью

;

Расстояние от точки да плоскости.

Пусть плоскость задана общим ур-нием . Расст. от до данной плоскости вычисляется по ф-ле

Вопрос №15. Цилиндры второго порядка.

Цилиндрическая поверхность-поверхность, описываемая прямой (образующей движущийся вдоль нек-рой линии направляющей) и остающейся параллельной исходному направлению.

Цилиндр второго порядка - цилиндрическая поверхность, направляющей к-рой явл. эллипс(окружность), гипербола или парабола.

Эллиптический цилиндр.

Гиперболический цилиндр

Параболический цилиндр.

Поверхности вращения второго порядка.

О Поверхностью вращения 2-го порядка наз пов-сть, образованная вращением линий 2-го порядка вокруг ее оси.

Эллипсоид вращения.

При вращении эллипса вокруг оси . Получим пов-сть, к-рая наз эллипсоидом вращения

Однополостный гиперболоид образуется при вращении гиперболы вокруг оси .

Двуполостный гиперболоид образуется при вращении гиперболы вокруг оси . .

К онус вращения: образуется вращением прямых вокруг оси .

Параболоид вращения: вращением вокруг оси

16. Понятие линейного пространства.

Линейным (векторным) пространством наз не пустое множество V с заданными на нём операциями сложения и умножения на число, удовлетв след условиям:

1) x+y=y+x для люб x,y ЄY

2)(x+y)+z=x+(y+z) для люб x,y,z ЄV

3) сущ-ет эл-т eЄV, такой что ; e – нулевой элемент

4) , y – противоположный эл-т

5) V

6)

7)

8) (

В дальнейшем под числами будем понимать только действительные числа, V – линейное пространство над полем действительных чисел. Эл-ты пространства V наз-ся векторами. Нулевой вектор - , противоположный x, как -x.

Нулевое векторное пространство – состоящее из одного нулевого вектора. - мн-во комплексных чисел, являющихся векторным пространством.

Лемма:

1) V сущ-ет единств нулевой эл-т

2) сущ-ет единств противоположный эл-т

3)

4)

5) если то либо =0, либо x =0.

6) - противоположный эл-ту x

Линейная зависимость и независимость векторов

Конечная с-ма векторов простр-ва V наз линейно зависимой, если найдутся такие числа , из кот-х хотя бы одно ≠0, такие что (совп с нейтральным эл-том).

В противном случае с-му наз линейно независимой.

Лемма. Система векторов простр-ва V явл-ся линейно зависимой, если один из векторов линейно выражается через остальные.

Выр-е вида наз линейной комбинацией векторов

Сис-ма векторов наз базисом пространства V , если:

1) с-ма векторов линейно независима

2)любой вектор пр-ва V линейно выр-ся через

Число n называется размерностью простр-ва V, если в этом пространстве сущ-ет n линейно независимых векторов, а любые n+1 векторы линейно зависимы.

Т. В простр-ве V разм-ти n любая с-ма, состоящая из n линейно независимых векторов, образует базис.

Если - базис простр-ва V, то называют разложением вектора x по векторам базиса. В этом случае наз координатами вектора x в базисе

Вопрос №17. Функция. Предел ф-и.

Ф-я. Рассм. множ-во элементов и множ-во элементов . Если каждому элементу из поставлен в соотв-е единственный элемент из обозначаем , то говорят: на множ-ве задана ф-я со значениями в множ-ве . Элементы значение аргумента; -значение ф-и; множ-во –область определения; множ-во всех значений ф-и – областью значений ф-и.

К основным способам задания ф-и относят:

1. Аналитический. Ф-я, заданная ф-лой , правая часть к-рой не содержит наз явной ф-ей. Ф-я наз заданной не явно.

2. Табличный способ- способ задания ф-ии при помощи таблицы (Н.:логарифмич. таблицы, тригонометрические и т.д.)

3. Графический-при помощи графика. Графиком ф-и наз множ-во точек плоскости с координатами плоскости , где .

сложная ф-я или композиция.

Степенные, показательные, логарифмические, тригонометрические, обратные тригонометрические наз основными элементарными ф-ями. Элементарными наз ф-ии, к-рые можно получить из основных элементарных с помощью алгебраических действий и композиций.