Вопрос №9.Системы линейных уравнений.

Совокупность ур-ний вида

(1) - с-ма –линейных ур-ний с –неизвестным

Числа наз коэф-ми с-мы. Числа - свободными коэфф-ми.

Решением с-мы (1) наз совокупность чисел при подстановке к-рых в с-му (1) вместо получаем верные числовые рав-ва.

Решить с-му, значит найти все ее решения, либо доказать, что их нет.С-ма наз совместной, если она имеет хотя бы одно решение, несовместной- если решений нет. Матрица составлена из коэф-тов

наз матрицей с-мы (1).

Если к данной матрице добавить столбец свободных коэф-тов, такую матрицу наз-ют расширенной матрицей с-мы

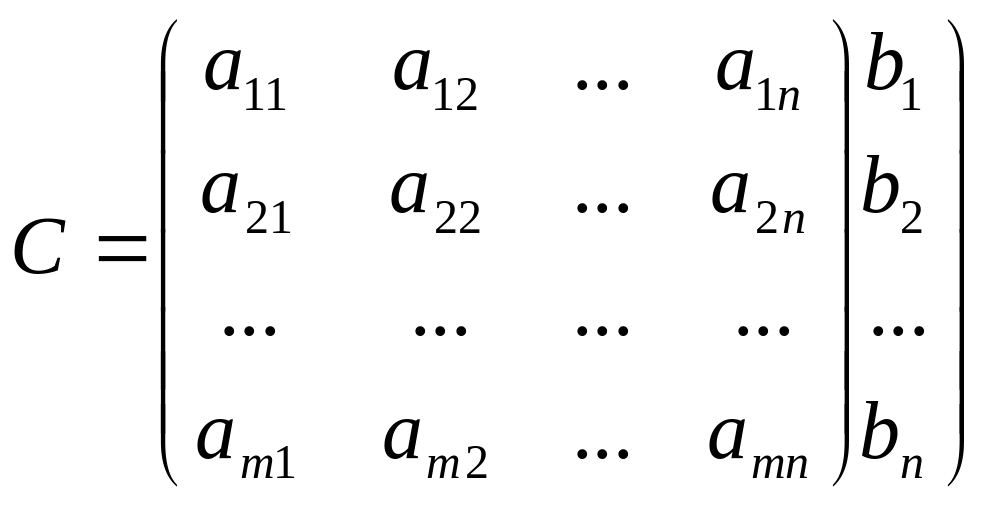Критерий совместимости с-мы.

Т.Кронекера-Копелли: Для того, чтобы с-ма линейных ур-ний была совместна необх и достаточно, чтобы ранг расширенной матрицы совпадал с рангом матрицы с-мы.

Метод Гаусса: применяется для произвольной с-мы линейных ур-ний.

С-му будем наз-ть ступенчатой, если матрица имеет ступенчатый вид. При решении с-м линейных ур-ний нам понадобится след алгоритм:

Запишем расшир. матрицу и приведем ее к ступенчатому виду.

если ранги не равны, то с-ма несовместна

если ранги равны и равны числу , то с-ма совместна и остается записать ее решение используя ступенчатый вид расширенной матрицы запишем соотв. ступенчатую с-му.

если = , совпад с числом неизвестных, то с-ма имеет единствен реш.

Двигаясь снизу вверх выражаем каждую из неизвестных.

если  , то в с-ме ур-ний и неизвестных. Неизвестные, к-рые первыми встречаются в ступенчатой с-ме ( -неизвестных) назовем главными неизвестными, а остальные –свободными неизвестными. Снизу вверх выражаем каждую из главных неизвестных свободные неизвестные могут принимать любые значения, в этом случае с-ма имеет бесконечно много решений.

Правила Крамера:

С-ма линейных ур-ний наз крамеровской, если число ур-ний совпадает с числом неизвестных и определитель матрицы с-мы отличен от 0.

Т. Крамеровская с-ма имеет единственное решение, к-рое находится по ф-лам

, где -определитель матрицы с-мы, а - определитель, полученный из  подстановкой вместо того столбца столбец свободных коэф-тов.

Матричный метод решения с-мы линейных ур-ний.

Этот метод основан на рав-ве .

Вопрос №10.Векторы и действия над ними.

Прямоуг. Декартова с-ма координат в пространстве.

Декартова с-ма корд. в пространстве определяется заданием масштабной единицы измерения длин и трех пересекающихся в одной точке 0 взаимноперпендик осей . О-начало координат. -ось абсцисс, -ось ординат, -аппликат.

Пусть М-произвольная точка пр-ва. Проведем через точку М 3 плоскости,  осям. Точки пересечения обозначим . Декартовыми коорд точки М в пр-ве наз числа , соотв. точкам .

Понятие вектора.

Любая упорядоченная пара точек А и В в пр-ве определяет направленный отрезок-вектор. А-начало вектора, В-конец вектора. Обозначают

Модуль вектора- его длина и обозн .Нулевой вектор-вектор, начало и конец кот совпадают. Единичный вектор-вектор, длина кот равна 1.

Вектора и наз коллинеарными если они лежат на параллельных прямых. Векторы и наз равными, если они коллинеарны и имеют равные длины. и наз противоположными , если они коллинеарны, противоположны и имеют равные длины.