Лабораторна робота 1.1 Дослідження проектування інтерфейсів з урахуванням методів квантифікації

Мета – навчитися проектувати інтерфейси з урахуванням методів квантифікації

Теоретичні відомості

Для кожної задачі завжди існують декілька варіантів рішення. За допомогою методів квантифікації інтерфейсів можна визначити переваги конкретного варіанту. Одним із найкращих підходів до кількісного аналізу моделей інтерфейсів є класична модель GOMS – «правила для цілей, об’єктів, методів і виділення» (the model of goals, objects, methods, and selection). Модель GOMS дозволяє передбачити, скільки часу буде потрібно досвідченому користувачеві на виконання конкретної операції під час використання конкретного інтерфейсу (табл. 1.1). GOMS – модель, що базується на оцінці швидкості друку.

Таблиця часових інтервалів операторів за моделлю GOMS

Таблиця 1.1

Операція	Опис
К= 0,2 с	Натиснення клавіші. Час, необхідний для того, щоб натиснути клавішу.
Р = 1,1 с	Вказівка. Час, необхідний користувачеві для того, щоб вказати на якусь позицію на екрані монітора.
Н=0,4 с	Переміщення. Час, необхідний користувачеві для того, щоб перемістити руку з клавіатури на ГПВ або з ГПВ на клавіатуру.
М=1,35 с	Ментальна підготовка. Час, необхідний користувачеві для того, щоб розумово підготуватися до наступного кроку.
R	Відповідь. Час, протягом якого користувач повинен чекати відповідь комп’ютера.

Основні правила розстановки ментальних операцій наведені в табл. 1.2.

Розстановка ментальних операцій

Таблиця 1.2

Правило	Опис
1. Початкова розстановка операторів M	Оператори M слід вставляти перед операціями К і P, призначеними для вибору команд; але перед операторами P, призначеними для вказівки на аргументи цих команд, ставити оператора M не слід.
2. Видалення очікуваних операторів М	Якщо оператор, що йде за оператором M, є повністю очікуваним з точки зору оператора, що передує M, то цей оператор M може бути видалений. Наприклад, переміщення ГПВ з наміром натиснути кнопку після досягнення мети руху. Відповідно до цього правила слід видалити оператор M, що був встановлений за правилом 0. У цьому випадку послідовність P M K перетворюється на P K.
3. Видалення операторів М усередині когнітивних одиниць	Якщо рядок M K M K M K... належить когнітивній одиниці, то слід видалити всі оператори M, крім першого. Когнітивною одиницею є безперервна послідовність символів, що вводяться, які можуть утворювати назву команди або аргумент. Наприклад Y, переміщати, або 4564.23 є прикладами когнітивних одиниць.
4. Видалення операторів M перед послідовними роздільниками	Якщо оператор K означає зайвий роздільник, що стоїть у кінці когнітивної одиниці (наприклад, роздільник команди, що слідує відразу за роздільником аргументу цієї команди), то слід видалити оператор M, що стоїть перед ним.

5. Видалення операторів M, які переривають команди

Якщо оператор K є роздільником, що стоїть після постійного рядка (наприклад, назва команди або будь-яка послідовність символів, яка кожного разу вводиться в незмінному вигляді), то слід видалити оператор M, що стоїть перед ним. (Додавання роздільника стане звичною дією, і тому роздільник стане частиною рядка і не вимагатиме спеціального оператора M.) Але якщо оператор K є роздільником для рядка аргументів або будь-якого іншого змінного рядка, то оператора M слід зберегти перед ним.

6. Видалення перекриваючих операторів M

Будь-яку частину оператора M, яка перекриває оператор R, що означає затримку, пов'язану з очікуванням відповіді комп'ютера, враховувати не слід.

Закон П.Фіттса (Paul M. Fitts) дозволяє кількісно визначити той факт, що чим далі знаходиться об'єкт від поточної позиції курсору або чим менше розміри цього об'єкта, тим більше часу потрібно для переміщення до нього (рис.1.1).

Математично закон Фіттса записується так:

Т = a + b log₂(D/S+1) ,

де Т– час на виконання дії(мс), S – розмір цілі, D – відстань до цілі.

Константи a і b встановлюються дослідним шляхом за параметрами продуктивності людини a=50, b=150

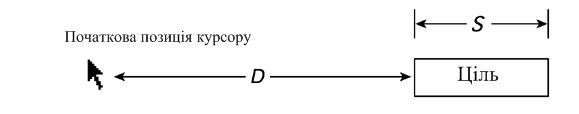
Рис. 1.1 Відстані, які використовуються в законі Фіттса для визначення часу, необхідного для переміщення курсору до цілі

Закон В. Хіка (William E. Hick) дозволяє кількісно визначити спостереження, що чим більше варіантів заданого типу, тим більше часу потрібно на його вибір (рис.1.2).

Рис.1.2 Залежність між часом і кількістю виборів

Математично закон Хіка записується так:

Т = a+b log₂(n+1),

де Т – середнє значення часу реакції (мс) за всіма альтернативами, п – кількість виборів з однаковою ймовірністю, а ,b – коефіцієнти пропорційності.

При використанні будь-яких позитивних і ненульових значень a і b із закону Хіка випливає, що надання користувачеві одразу кількох варіантів одночасно зазвичай є більш ефективним, ніж організація тих самих варіантів в ієрархічні групи. Наприклад, вибір з одного меню, що складається із восьми елементів, проводиться швидше, ніж із двох меню, що складаються з чотирьох елементів кожне.

Отже, час реакції з вибору деякого числа альтернатив залежить від їх кількості.

Ефективність інтерфейсу - це відношення мінімальної (М) кількості інформації, необхідної для виконання завдання, до кількості інформації, яку повинен ввести користувач (F):

Е=M/F,

де M(F) ­– мінімальна (фактична) ­­ кількість інформації розраховується за формулою:

М=К*Log₂(N),

де K – кількість жестів, N– кількість варіантів вибору.

Наприклад, потрібно підрахувати на калькуляторі (рис.1.3) остачу від ділення. Для цього послідовно натискаємо 256%101=

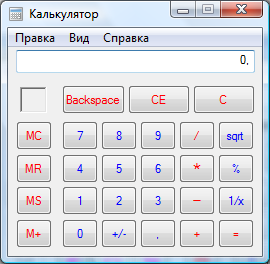
Рис.1.3 Калькулятор

Для виконання поставленого завдання користувачеві необхідно зробити К=8 жестів. При виконанні кожного з них є N=2 варіанти: натиснути ліву або праву кнопку миші. Тому M= 8*Log₂ 2 =8 біт.

Для підрахунку кількості інформації (F), яку повинен ввести користувач, необхідно виділити з робочої області додатка кількість областей, натискання миші в котрих можливе. У нашому випадку таких областей (варіантів) N=28. Для виконання поставленого завдання користувачеві необхідно зробити 8 жестів. F= 8* Log₂ 28 =~40 біт, отже,

Е=8/40=0,2

Додаткові відомості: [9, глава 4].