1.Основные понятия и гипотезы сопротивления материалов.
Все твердые тела в той или иной мере обладают прочностью и жесткостью.
Сопротивление материалов – наука о прочности и жесткости элементов инженерных конструкций.
Рассмотрим некоторое пространственное тело, находящееся в равновесии под действием системы сил. Тело деформируется, и его точки К получают перемещения (рис. 1.1, а).
Выделим в окресности точки К бесконечно малый элемент размерами dx, dy, dz (рис.1.1, б).
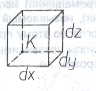
В пространстве эта точка имеет шесть степеней свободы: три поступательных (линейных) и три вращательных (угловых) перемещения. Деформация тела взаимосвязана с деформацией отдельных элементов.
При деформации тела его элементы оказывают давление друг на друга. Эти давления называются напряжениями.
Между напряжениями, деформациями и перемещениями существуют определенные зависимости. Для установления этих зависимостей вводятся ряд допущений, гипотез и принципов.
1. Тело считается сплошным, т.е. не имеет никаких пустот и трещин.
2. Материал тела считается однородным. Свойства бесконечно малого элемента не зависят от его расположения в теле.
3. Материал тела считается изотропным, т.е. имеет одинаковые физические свойства во всех направлениях.
Но дерево обладает разными физическими свойствами вдоль и поперек волокон. Подобные материалы называют анизотропными.
4. Деформации тела считаются упругими.
5. Деформации тела считаются малыми, т.е. перемещения точек весьма малы по сравнению с размерами всего тела.
6.Тело считается линейно-деформируемым, т.е. деформации, напряжения и перемещения возрастают пропорционально (линейно) росту нагрузки.
2.Метод сечений для определения внутренних сил в брусе.
Рассечем брус плоскостью, перпендикулярной к оси бруса в точке К, и рассмотрим равновесие одной из частей (рис. 2.6, б).
Рассечем брус плоскостью, перпендикулярной к оси бруса в точке К, и рассмотрим равновесие одной из частей (рис. 2.6, б).
Часть В должна находиться в равновесии под действием внешних сил Р3 и Р4 и поля элементарных сил dP, действующих по элементарным площадкам dF поперечного сечения.
Все элементарные силы, действующие в сечении, можно привести к главному вектору и главному моменту в системе координат x, y, z.
Представляя главный вектор в виде составляющих N , Qx , Qу и главный момент в виде составляющих Мx , Му , Мz , получим внутренние силы :
N - продольная сила,
Qx , Qу - поперечные силы,
Мx , Му - изгибающие моменты,
Мz = Мкр - крутящий момент.
Внутренние силы можно рассматривать и как интегральные характеристики поля напряжений, действующих в сечении.
3.Дифференциальные и интегральные зависимости между интенсивностью распределённой нагрузки и внутренними силами
Участком оси бруса назовем часть оси бруса между двумя соседними узловыми точками. Узловой назовем точку, в которой изменяет свой характер либо ось бруса либо нагрузка (например, приложена распределенная нагрузка, сосредоточенная сила или момент), либо изменяется поперечное сечение.
На каждом участке любая внутренняя сила S представляет собой функцию S(s).
Вырежем из бруса двумя сечениями l – l и ll – ll элемент плоского бруса длиной dz (рис. 2.10, а).
Обозначим интенсивность
поперечной нагрузки - q,
продольной нагрузки - qn ,
изгибающего момента - m.
Элемент бруса находится в равновесии, то из условий статики получим:
Пренебрегая членами высшего порядка малости, получим:
Рассмотрим теперь элемент dz бруса, на который действует распределенной крутящий момента mz относительно оси z (рис.2.10, б).
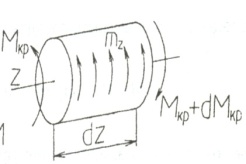
На основе полученных дифференциальных зависимостей можно установить и интегральные зависимости между внутренними силами и нагрузкой.