
- •1. Собственные интегралы, зависящие от параметра.
- •2. Формула Лейбница.
- •3. Несобственные интегралы, зависящие от параметра.
- •4. Признак Вейерштрасса равномерной сходимости по параметру.
- •5 . Гамма функция. Свойства.
- •6. Бета функция. Свойства.
- •7.Интеграл Фурье.
- •8.Двойной интеграл. Определение. Примеры.
- •9.Сведение двойного интеграла к повторному.
- •10.Замена переменных в двойном интеграле. Якобиан.
- •11.Тройные и n кратные интегралы.
- •12.Криволинейный интеграл первого рода.
- •13.Криволинейный интеграл второго рода.
- •14.Формула (теорема) Грина.
- •15.Независимость криволинейного интеграла второго рода от пути интегрирования.
- •16.Элементы теории поверхностей.
- •17.Поверхностные интегралы первого рода.
- •18.Поверхностные интегралы второго рода.
- •19.Дивергенция векторного поля.
- •20. Теорема Остроградского-Гаусса.
- •21.Векторные тождества.
- •22.Потенциальные и соленоидальные поля.
- •24.Формула Стокса.
- •25. Дифференциальные уравнения.
19.Дивергенция векторного поля.
![]()
Свойства дивергенции
![]()
![]()
![]()
20. Теорема Остроградского-Гаусса.
Для
вычисления потока через внешнюю сторону
замкнутой поверхности ![]() удобно применить формулу Остроградского
– Гаусса:
удобно применить формулу Остроградского
– Гаусса:
![]() ,
(5)
,
(5)
где  –
дивергенция векторного поля
–
дивергенция векторного поля ![]() в
точке
в
точке ![]() .
.
Поток
будет равен тройному интегралу от ![]() ,
взятому по объему
,
взятому по объему ![]() ,
ограниченному поверхностью
,
ограниченному поверхностью ![]() .
.
Если
в пространстве задано векторное поле
и
линия ![]() ,
то работа этого поля вдоль линии
,
то работа этого поля вдоль линии ![]() представляет собой криволинейный
интеграл
представляет собой криволинейный
интеграл ![]()
21.Векторные тождества.
Введём
обозначение:
 – формальный оператор,
– формальный оператор,
 – оператор Гамильтона.
– оператор Гамильтона.
Пусть
u–
скалярное поле. Тогда
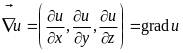 .
.
Пусть
 – векторное поле. Тогда
– векторное поле. Тогда
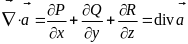 .
.
 .
.
22.Потенциальные и соленоидальные поля.
Потенциальные векторные поля
Для
того, чтобы поле
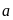 было потенциальным в области G,
необходимо и достаточно , чтобы выполнялось
одно из условий:
было потенциальным в области G,
необходимо и достаточно , чтобы выполнялось
одно из условий:
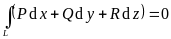 для любой замкнутой
кривой L.
для любой замкнутой
кривой L.
Для
любых двух кривых, у которых совпадают
начала и концы,
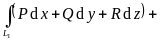
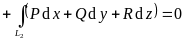 .
.
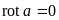 .
.
Первые
два условия эквивалентны. Докажем второе
условие: пусть
 .
Тогда
.
Тогда
 (по тереме
о среднем)
(по тереме
о среднем)
 ,
где
,
где
 .
Тогда
.
Тогда
 .
Аналогично
.
Аналогично
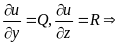 поле
потенциально.
поле
потенциально.
Соленоидальные векторные поля
Векторное
поле
называется соленоидальным, если для
любой замкнутой поверхности ,
ограничивающей некоторое тело V,
 .
.
Поле
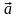 соленоидально тогда и только тогда,
когда
соленоидально тогда и только тогда,
когда
 .
.
Пусть
.
Тогда по теореме Остроградского
 .
.
Пусть
– соленоидально, т.е.
.
Пусть
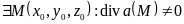 .
Тогда существует сфера
.
Тогда существует сфера
 и
и
 при
при
 ,
т.е.
,
т.е.
 .
Пусть
– поверхность V.
Тогда по теореме Остроградского
.
Пусть
– поверхность V.
Тогда по теореме Остроградского
 ,
что противоречит тому, что поле
соленоидально, следовательно,
.
,
что противоречит тому, что поле
соленоидально, следовательно,
.
Если
поле
соленоидально, то существует векторное
поле
 .
.
23.Ротор
векторного поля.
![]() или
в символическом виде
или
в символическом виде
Свойства ротора
![]()
![]()
![]()
24.Формула Стокса.
Формула Стокса
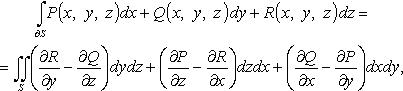
обход
контура ![]() (границы
поверхности S)
согласован с выбором стороны поверхности S.
(границы
поверхности S)
согласован с выбором стороны поверхности S.
Формула Стокса в символической форме
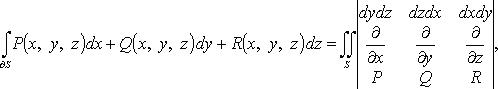
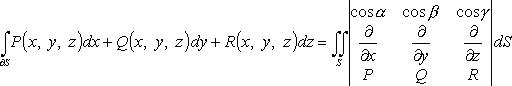
(![]() -
направляющие косинусы нормали,
соответствующей выбранной стороне
поверхности.
-
направляющие косинусы нормали,
соответствующей выбранной стороне
поверхности.
25. Дифференциальные уравнения.
Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке. Дифференциальное уравнение содержит в своей записи неизвестную функцию, её производные и независимые переменные; однако не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением.
Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
![]()
где p(x) и h(y) −
непрерывные функции.
Рассматривая
производную y' как
отношение дифференциалов ![]() ,
перенесем dx в
правую часть и разделим уравнение
на h(y):
,
перенесем dx в
правую часть и разделим уравнение
на h(y):
![]()
Разумеется,
нужно убедиться, что h(y)
≠ 0. Если найдется число x0,
при котором h(x0)
= 0, то это число будет также являться
решением дифференциального уравнения.
Деление на h(y) приводит
к потере указанного решения.
Обозначив ![]() ,
запишем уравнение в форме:
,
запишем уравнение в форме:
![]()
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
![]()
где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение
![]()
описывающее общее решение уравнения с разделяющимися переменными.
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
![]()
где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
Использование интегрирующего множителя;
Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
то интегрирующий множитель определяется формулой:
![]()
Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение диффференциального уравнения выражается в виде:
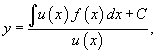
где C − произвольная постоянная.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
![]()
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Алгоритм решения уравнения в полных дифференциалах
Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
![]()
Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):
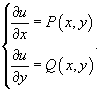
Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
![]()
Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:
![]()
Отсюда получаем выражение для производной неизвестной функции φ(y):
![]()
Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):
Общее решение уравнения в полных дифференциалах записывается в виде:
![]()
Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ(x).
Для линейных
неоднородных уравнений с постоянными
коэффициентами и с правой частью
специального вида, а именно состоящей
из сумм и произведений функций ![]() ,
частное решение можно искать методом
неопределенных коэффициентов.
Вид частного решения зависит от корней
характеристического уравнения. Ниже
представлена таблица видов частных
решений линейного неоднородного
уравнения с правой частью специального
вида.
,
частное решение можно искать методом
неопределенных коэффициентов.
Вид частного решения зависит от корней
характеристического уравнения. Ниже
представлена таблица видов частных
решений линейного неоднородного
уравнения с правой частью специального
вида.
Правая часть |
Число, сравниваемое с корнем характеристического уравнения |
Вид частного решения |
|
0 - не корень |
|
0 - корень кратности k |
|
|
|
|
|
- корень кратности k |
|
|
|
|
|
- корень кратности k |
|
|
|
|
|
- корень кратности k |
|
Здесь ![]() -многочлены степени s,
а
-многочлены степени s,
а ![]() -
многочлены степени s,
коэффициенты которых нужно найти методом
неопределенных коэффициентов. Для того
чтобы их найти, нужно функцию, задающую
вид частного решения, подставить в
исходное дифференциальное уравнение
и после приведения подобных слагаемых
приравнять соответствующие коэффициенты
в правой и левой частях уравнения.
-
многочлены степени s,
коэффициенты которых нужно найти методом
неопределенных коэффициентов. Для того
чтобы их найти, нужно функцию, задающую
вид частного решения, подставить в
исходное дифференциальное уравнение
и после приведения подобных слагаемых
приравнять соответствующие коэффициенты
в правой и левой частях уравнения.
