10.Замена переменных в двойном интеграле. Якобиан.

Для вычисления двойного интеграла иногда удобнее перейти в другую систему координат. Это может быть обусловлено формой области интегрирования или сложностью подынтегральной функции. В новой системе координат вычисление двойного интеграла значительно упрощается. Замена переменных в двойном интеграле описывается формулой

где выражение представляет собой так называемый якобиан преобразования , а S − образ области интегрирования R, который можно найти с помощью подстановки в определение области R. Отметим, что в приведенной выше формуле означает абсолютное значение соответствующего определителя.

11.Тройные и n кратные интегралы.

Предел интегральных сумм (f,, ) при ()0 (если он существует и не зависит от выбора разбиений и промежуточных точек ) называется тройным интегралом от функции f на D и обозначается

= .

Можно использовать обозначение = .

Более точно это определение выглядит следующим образом:

J>0>0:(()<, )|(f,, )-J|<.

Понятие длины, площади, объема распространяется и на области n- мерного евклидова пространства. В этом случае говорят об измеримости множества D n- мерного пространства и о его мере D. Для измеримой области D и определенной на ней функции f(x)=f(x1,x2,…,xn) рассматривается разбиение этой области на измеримые множества {Dk}. В каждой из подобластей выбераются промежуточные точки k=( )Dk. Полученный набор точек обозначим  ={k}. Интегральной суммой для набора f, ,  называется выражение

(1)

Суммирование производится по всем областям разбиения. Величина ()= d Dk называется характеристикой разбиения  (d Dk – диаметр множества ).

Определение. Предел интегральных сумм (f,, ) при ()0 (если он существует и не зависит от выбора разбиений и промежуточных точек ) называется тройным интегралом от функции f на D и обозначается

= .

12.Криволинейный интеграл первого рода.

Определение

Пусть кривая C описывается векторной функцией , где переменная s представляет собойдлину дуги кривой (рисунок 1). Если на кривой C определена скалярная функция F, то интеграл называется криволинейным интегралом первого рода от скалярной функции F вдоль кривой C и обозначается как

Криволинейный интеграл существует, если функция F непрерывна на кривой C.


Рис.1		Рис.2

Свойства криволинейного интеграла первого рода

Криволинейный интеграл I рода обладает следующими свойствами:

Интеграл не зависит от ориентации кривой;

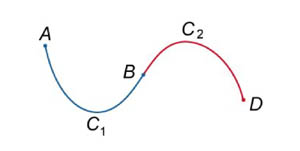
Пусть кривая C₁ начинается в точке A и заканчивается в точке B, а кривая C₂ начинается в точкеB и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться криваяC₁ U C₂, которая проходит от A к B вдоль кривой C₁ и затем от B к D вдоль кривой C₂. Для криволинейных интегралов первого рода справедливо соотношение