Формула полной вероятности

Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.

Формулировка

Пусть дано вероятностное пространство  , и полная группа попарно несовместных событий  , таких что            . Пусть   — интересующее нас событие. Тогда

.

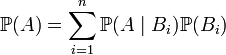Замечание

Формула полной вероятности также имеет следующую интерпретацию. Пусть   — случайная величина, имеющаяраспределение

.

Тогда

,

т.е. априорная вероятность события равна среднему его апостериорной вероятности.