Числовые характеристики случайных величин и векторов

В данном разделе определяются основные числовые характеристики случайных величин и векторов – математическое ожидание , дисперсия, ковариация, коэффициент корреляции и т.д.

Интеграл Лебега – математическое ожидание

Пусть основное вероятностное пространство и случайная величина. Наша цель – определить интеграл Лебега от случайной величины

который в теории вероятностей называется математическое ожидание (среднее значение) случайной величины

Вначале определим этот интеграл для простых случайных величин.

Если случайная величина простая

то интегал Лебега от простой случайной величины определяется так

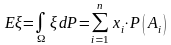
В частности

Ясно, что, таким образом определенный, интеграл обладает следующими очевидными свойствами

Свойства интеграла Лебега (математического ожидания)

1. 

2. 

3. 

4. 

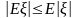
5. для независимых случайных величин

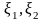
Доказательство последнего свойства следует из того, что для независимых случайных величин

Пусть теперь случайная величина неотрицательна. Тогда для нее существует последовательность простых случайных величин монотонно приближающая ее снизу.

Интеграл Лебега определим как предел интегралов от простых случайных величин.

Заметим, что так как последовательность интегралов от монотонно возрастающих функций тоже монотонно возрастает, у этой последовательности обязан быть предел, пусть даже равный бесконечности. Можно показать, что этот предел не зависит от последовательности приближающих простых случайных величин, т.е. определение корректно.

Для произвольной случайной величины положим

если хотя бы один из этих интегралов конечен.

Скажем, что у случайной величины конечное математическое ожидание, если конечны оба этих интеграла, или что то же самое, конечен интеграл

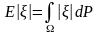
Свойства интегралов от простых случайных величин переносятся на случай произвольных случайных величин без изменений.

Заметим, что свойство нормированности вероятности 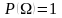при построении интеграла не использовалось. Таким образом можно строить интегралы по произвольным мерам.

Неравенства Неравенство Маркова

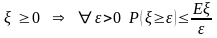
Доказательство следует из очевидного неравенства

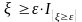
и свойств 1) и 3) математического ожидания.

Неравенство Чебышева. Дисперсия

Доказательство следует из неравенства Маркова, примененного к случайной величине .Величина называется дисперсия случайной величины. Она является естественной мерой разброса случайной величины относительно ее математического ожидания. Очевидны следующие свойства дисперсии.

1. 

2. 

3. для независимых с.в.

Следующее свойство выявляет смысл математического ожидания и дисперсии, как экстремальных характеристик с.в. Будем обозначать точку экстремума (минимума и максимума) функции так

. Тогда

Для доказательства заметим, что по переменной x выражение 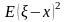представляет собой квадратный трехчлен.

Неравенство Коши-Буняковского-Шварца. Ковариация

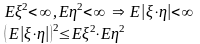
Доказательство. Если то и неравенство превращается в равенство.

Если то, используя очевидное неравенство 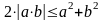получаем

что эквивалентно доказываемому неравенству.

Применяя неравенство КБШ к случайным величинам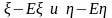 получаем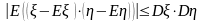

Величина называется ковариация случайных величин и, как мы увидим в дальнейшем, является естественной мерой связи этих случайных величин между собой. Величина

называется коэффициент корреляции случайных величин Из неравенства КБШ следует, что и если то между этими случайными величинами существует (почти наверное) линейная зависимость

с положительным коэффициентом a. В этом случае говорят, что случайные величины положительно коррелированы. Если

то коэффициент a отрицателен и случайные величины отрицательно коррелированы. Коэффициент корреляции используют как меру зависимости случайных величин.