5.6. Математичне забезпечення операцій на грошовому ринку
5.6.1. Основні умовні позначення
і (%) - проста річна ставка відсотка;
і - відносна проста річна ставка відсотка;
іс- відносна величина річної ставки складних відсотків;
j - номінальна ставка складних відсотків;
Іг - сума відсоткових грошей, виплачених на рік за відсотками;
І - загальна сума відсоткових грошей, сплачена за ставкою відсотка за весь період нарахування;
D (%) - проста річна облікова ставка;
d - відносна величина простої облікової ставки;
dc(%) - складна річна облікова ставка;
dc- відносна величина складної річної облікової ставки;
f- номінальна річна облікова ставка;
Dr - сума відсоткових грошей, сплачених на рік за обліковою ставкою;
D - загальна сума відсоткових грошей, сплачених за обліковою ставкою за весь період нарахування;
Р - величина початкової вкладеної грошової суми;
S - нарощена сума;
Кн - коефіцієнт нарощення у випадку простих відсотків;
Кн.с- коефіцієнт' нарощення у випадку складних відсотків;
Кн.у- коефіцієнт нарощення у випадку облікових ставок;
kд - коефіцієнт дисконтування;
n - період нарахування в роках;
д - період нарахування в днях;
К - тривалість року в днях;
аr - річний темп інфляції;
а - темп інфляції;
іа- ставка відсотків, яка враховує інфляцію;
Sa - сума, покупна спроможність якої з урахуванням інфляції дорівнює покупній спроможності суми S при відсутності інфляції;
Ін - індекс інфляції;
R - величина кожного платежу ануїтету (фінансова рента);
А - сучасна величина ануїтету;
Ходаківська В. 11., Беляєв В. В
kн.a -коефіцієнт нарощення ануїтету;
а- коефіцієнт приведення ануїтету;
N - номінальна вартість акції або облігації;
Р0 - вартість покупки облігації;
Pk-курс облігації;
Іо - дохід за облігацією;
Pa - вартість покупки акції;
Q - ціна продажу акцій;
la - дохід за акціями.
5.6.2. Основні поняття та формули
Процентними грошима (відсотками) називають суму доходів від надання грошей у різних формах (відкриття депозитних рахунків, видача кредитів, купівля облігацій і т. д.).
Збільшення суми боргу за рахунок нарахованих відсотків називається нарощенням (ростом) початкової суми боргу.
Відношення нарощеної суми до початкової суми боргу називають коефіцієнтом нарощення.
Інтервал часу, за який нараховують відсотки, називають періодом нарахування.
Концепція тимчасової вартості грошей
Стара приказка про те, що краще синиця в руках, аніж журавель у небі, безпосередньо стосується фінансів. Це означає, що сьогодні гроші мають більшу вартість, ніж завтра: з плином часу вартість грошей змінюється. Інвестори, звісна річ, віддають перевагу грошам, які с сьогодні, а не тим, що будуть завтра, бо вони дають їм змогу з тих грошей зробити ще гроші. Це, звичайно, основна мета фінансового менеджера. Окрім тої о, що гроші сьогодні мають більшу вартість, ніж гроші в майбутньому, слід ще пам'ятати, що вони з часом частково втрачають свою вартість. Основні причини втрати вартості ірошей:
• інфляція;
• ризик;
• схильність до ліквідності.
Одним з найважливіших інструментів проведення аналізу тимчасової вартості грошей є часова лінія. Графічний вираз тим-
188
ринок фінансових послуг: теорія і практика часового розподілу потоку готівки відтворює діаграма А:
Діаграма А
Кожний штрих на лінії відмічає кінець одного періоду і, в той же час, початок наступного. Іншими словами, штрих І на часовій лінії відмічає кінець року 1 і початок року 2.
Діаграма В
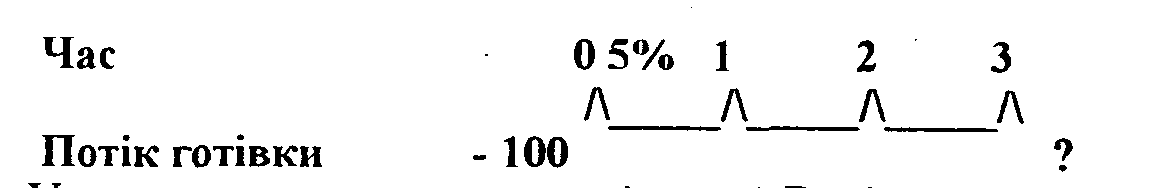
У випадку, показаному на діаграмі В, відсоткова ставка
для усіх трьох періодів становить 5 відсотків. Під час 0 трапився одноразовий відплив потоку готівки, під час 3 очікується невідомий приплив готівки. Відплив - це витрати, виплати, депозити готівкою. Приплив - прийняття готівки.
Діаграма С
На діаграмі С відсоткова ставка у перший період становить 5 відсотків, але протягом другого періоду вона виросте до 10 відсотків. Якщо відсоткова ставка постійна протягом усіх періодів, ми вказуємо її тільки для першого періоду, якщо ж вона змінюється, то її вказують для кожного періоду окремо.
Часові лінії дуже важливі для початкового розуміння концепцій тимчасової вартості грошей, але навіть досвідчені спеціалісти користуються нею для проведення складного аналізу проблем.
Долар, який ми маємо наданий момент, коштує дорожче, ніж долар, отриманий у майбутньому. Це відбувається тому, що якщо ви маєте його зараз, то можете його вкласти у будь-яку справу і одержати відсоток, що однаково дасть суму, більшу ніж долар, який ви отримаєте у майбутньому.
Майбутня вартість - сума, до якої виросте грошовий потік чи серія грошових потоків протягом даного періоду часу при даній процентній ставці. Цей процес продовжується, і внаслідок того, що кожного разу початкова сума вище попередньої, річний відсоток зростає.
189
Ходаківська В. II., Веляєв В. В
Процес переходу від теперішньої вартості (Р) до майбутньої вартості (S) називається компаундируванням.
Приклад. Припустимо, що ви поклали у банк 100 доларів під 5 відсотків річних. Яку суму ви будете мати наприкінці першого року? S у такому випадку необхідно розраховувати наступним чином:
S = Si = Р + Рі = Р (1 + і) = S 100 (1 + 0,05) = $ 100 (1,05) = S 105.
S = Р (1 + пі) .
Відповідно до цього рівняння майбутня вартість після закінчення одного року дорівнює початковій ставці, помноженій
на 1,0 плюс відсоткова ставка.
Яким же буде результат, якщо ви залишите свої 100 доларів на банківському рахунку на 5 років? Для того, щоб краще не зоозуміти, слід накреслити часову лінію:
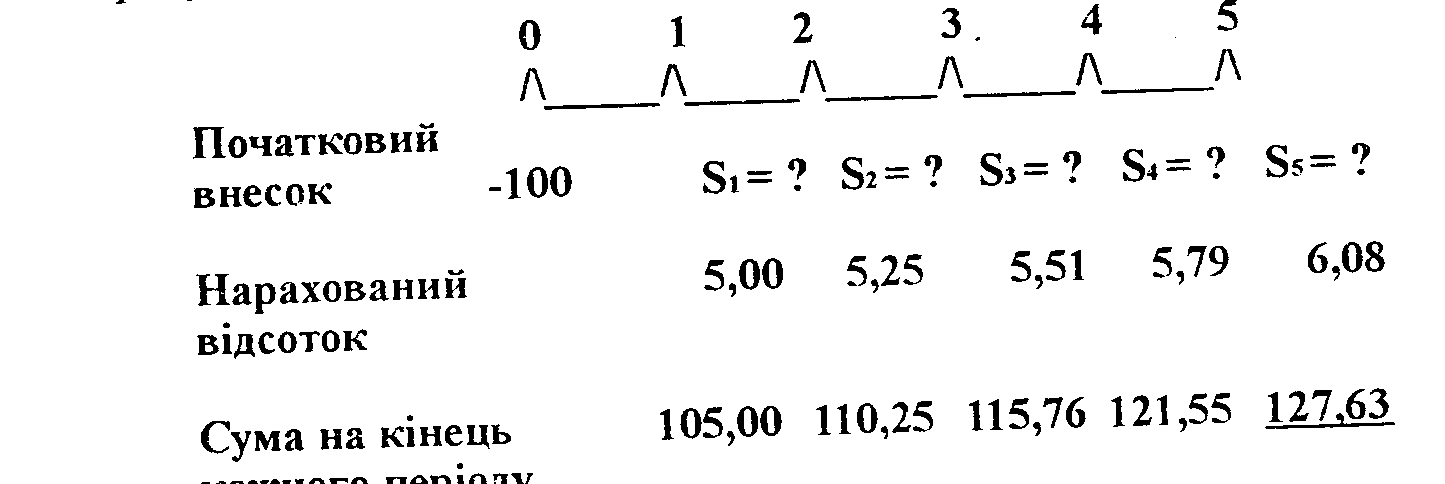
Відмітьте, що вартість наприкінці 2 року, $ 110/25,дорівнює
S;°= S, (1 + і) = Р (1 + і) (1 + і) = Р (1 + і);= S 100 (1,05), = S 110,25.
Кінцевий результат третього року внеску:
S,= Si (1 + і) = P(l + і) (1 + і) (1 + і) = Р(1 + і)і= S 100 (1,05> = S 115,76.
1, нарешті:
S.= S< (1+ і) = Р (1 + і) (1 + і) (1 + і) (1 + і) (1 + і) = Р (1 + і). = S 100 (1,05)з -- S 127.63.
Взагалі, майбутня вартість початкової суми на кінець п-ої кількості років може бути визначена за допомогою рівняння:
S = Р (1 + і)п.
Поняття поточної вартості. Припустимо, що у вас з'явились вільні гроші, 100 доларів США, і ви маєте можливість придбати цінні папери з низьким відсотком ризику, за якими через 5 років отримаєте 127,63 долара. Ваш місцевий банк на даний час пропонує 5 відсотків річних за внеском на 5 років, і ви вважаєте, що ці цінні папери такі ж надійні, як і ощадні сертифікати. Ставка 5 відсотків може бути визначена як ставка "ціни шансу"
190
ринок фінансових послуг: теорія і практика
або ставка прибутку, який ви могли б одержати за іншим внеском з таким же ступенем ризику. Отже, запи тання: яку суму ви були б згодні заплатити за дані цінні папери?
З прикладу майбутньої вартості ми зрозуміли, що первісна сума в 100 доларів США, покладена в банк під 5% річних, після закінчення 5 років матиме вартість у 127,63 долара США. 100 доларів США у даному випадку визначаються як поточна вартість (Р) суми в 127,63 долара США у майбутньому, через 5 років.
Поточна вартість потоку готівки, очікувана через п-у кількість років у майбутньому - це сума, яка (якщо є в наявності на сьогодні), виросте до рівня суми, що дорівнює майбутній. Через те, що S 100 при 5-процентній річній ставці виросте за 5 років до суми $ 127,63, то $ 100 е поточною вартістю суми S 127,63 при 5-процентній ставці та за 5 років.
Дія визначення поточної вартості називається дисконтуванням і є прямою протилежністю компаундируванню.
Поточна вартість 1 долара США (або будь-якої іншої суми), яку вкладник очікує отримати у майбутньому, графічно зменшуватиметься із плином часу відповідно до того, як збільшуються показники років. При відносно високій відсотковій ставці сума, яку вкладник розраховує одержати в майбутньому, коштує в поточний момент небагато. Навіть якщо відсоткова ставка низька, поточна вартість суми, що повинна виплатитись через досить довгий час, досить мала. Наприклад, при 20-відсотковій дисконтній ставці 1млн. доларів через 100 років буде мати вартість усього 1 цента сьогоднішнього дня (проте 1 цент при 20-відсотковій ставці за 100 років виросте до 1млн. доларів).
Розрахунки тимчасової вартості грошей майже завжди виконуються за допомогою рівнянь із чотирма невідомими. Тому, якщо вам відомо три з них, ви (або ваш калькулятор) можете легко розрахувати четверту. Так, якщо вам відомі суми окремих потоків готівки і Р (або S) всього потоку готівки, ви можете розрахувати відсоткову ставку.
На практиці значно частіше, ніж раз на рік, проводяться виплати та нараховуються відсотки, тому кількість років необхідно замінити в таких випадках на кількість періодів.
Поняттями, розглянутими вище, ми будемо користуватись при обміркуванні проблем прийняття фінансових рішень у різних фінансових ситуаціях з використанням рівнянь із чотирма невідомими.
191
Ходаківська В. 11., Беляєв В. В
Декурсивний та антисипативний способи нарахування відсотків
Існує дві концепції і, відповідно, два способи визначення і
нарахування процентів.
Антисипативтш (попередній) спосіб. Відсотки нараховуються на початку кожного інтервалу нарахування. Сума процентних грошей визначається, виходячи із нарощеної суми:
S = Р/(1 - і)n.
Відсотковою ставкою буде виражене у відсотках відношення суми прибутку, що сплачується за певний інтервал, до величини нарощеної суми, яка отримується в кінці цього інтервалу. Ставка, що визначається таким способом, називається (в широкому розумінні) обліковою ставкою або антисипативним відсотком.
Декурсивний спосіб. Відсотки нараховуються в кінці кожного інтервалу нарахування. Декурсивна відсоткова ставка або позичковий відсоток - це відношення суми нарахованого за певний інтервал доходу до суми, що є на початку даного інтервалу.
У світовій практиці Декурсивний спосіб найбільш розповсюджений. У нас - антисипативний, особливо в періоди високої інфляції. При рівності позичкового відсотку та облікової ставки, нарощення початкової суми в другому випадку (антисипативний спосіб) йде швидше, тому в літературі часто можна зустріти твердження, що Декурсивний спосіб більш вигідний для позичальника, а антисипативний - для кредитора. Але це справедливо лише
для невеликих відсоткових ставок.
Приклад. Початкова сума боргу складає 3800 грн. Визначити величину нарощеної суми через 4 роки при застосуванні де-курсивного і антисипативного способів нарахування відсотків. Річна ставка - 70%.
Декурсивний спосіб:
S = 3800 (1 + 0,7)4 = 31738.
Антисипативний спосіб:
S = 3800 / (1 - 0,7)4 = 475 000.
Даний приклад демонструє різницю у результатах при різних способах нарахування відсотків на фоні великих сум і високих відсоткових ставок.
Прості ставки позичкових відсотків (декурсивних) застосовуються у короткотермінових фінансових операціях, коли інтервал нарахування співпадає з періодом нарахування (і складає, як правило, термін менше одного року). Звичайно, прості ставки по-
192
ринок фііілисоиііх послуг: теорія і практика.
зичкових відсотків можуть застосовуватись і в будь-яких інших випадках за домовленістю сторін, що беруть участь в угоді.
Залежно від способу визначення тривалості фінансової операції розраховується точний або звичайний (комерційний) відсоток. Точний відсоток отримують, коли за часову базу приймають фактичну кількість днів на рік (365 або 366) і точну кількість днів позички. Дата видачі та дата погашення позички завжди рахуються як один день.
У практиці банків різних країн термін у днях і розрахункова кількість днів на рік при нарахуванні відсотків визначається по-різному. Німецька практика підрахунку кількості днів засновується на тривалості року в 360 днів і місяців у ЗО днів. При французькій практиці тривалість року приймається рівною 360 дням, а кількість днів на місяць береться рівного їх фактичній календарній тривалості (28, 29, ЗО і ЗІ день відповідно). В англійській практиці рік береться тривалістю у 365 днів і відповідна точна тривалість місяців. При використанні простих відсотків сума процентних грошей протягом всього терміну боргу визначається виходячи із початкової суми боргу, незалежно від кількості періодів нарахування та їх тривалості.
Ходаківська В.П., Бсляєв В. В
Для випадків простих облікових ставок. При антисипа-тивному способі нарахування відсотків сума отримуваної о доходу розраховується виходячи із суми, що отримується після закінчення певного інтервалу нарахування (тобто із нарощеної суми). Ця сума і вважається величиною отримуваного кредиту (або позички). Так як у даному випадку відсотки нараховуються на початку кожного інтервалу нарахування, позичальник, звичайно, отримує цю суму за вирахуванням процентних грошей (S — Р). Така операція називається дисконтуванням за обліковою ставкою, а також комерційним або банківським обліком.
Дисконтом називається дохід, отриманий за обліковою ставкою, тобто різниця між розміром кредиту і сумою, що видається.
На практиці облікові ставки застосовуються, в основному, при обліку (купівлі) векселів та інших грошових зобов'язань.
Складні ставки позичкових відсотків. Якщо після чергового інтервалу нарахування дохід (нараховані за даний інтервал відсотки) не виплачується, а додається до грошової суми, що є на початку цього інтервалу, то для визначення нарощеної суми застосовують формули складних відсотків, які є досить розповсюдженим сьогодні видом відсоткових ставок, що застосовуються у різних фінансових операціях.
Коли виникає можливість вибору між низькою складною відсотковою ставкою і більш високою простою, слід віддавати перевагу першому варіанту.
194
У нашій країні на даний момент наиоільш розповсюджу ним є нарахування відсотків за півріччями, поквартальне щомісячне. Такі відсотки,, що нараховуються з певної періодичністю, називаються дискретними.
У світовій практиці часто застосовується також неперері не нарахування складних відсотків (тривалість інтервалу нарах;
вання прагне до нуля, a m - до нескінченності): е = 2/71828.... S = Р е„
Формули еквівалентності облікових ставок. Оскільки умови нарахування відсотків с одним з основних факторів при виборі банку або фінансової компанії дпя розміщення засобів, необхідно їх порівнювати за деяким загальним показником. У якості такої о показника використовується еквівалентна (ефективна) річна ставка простих або складних відсотків.
Еквівалентні відсоткові ставки - це такі ставки різного виду, застосування яких при "різних початкових умовах дає однакові фінансові результати.
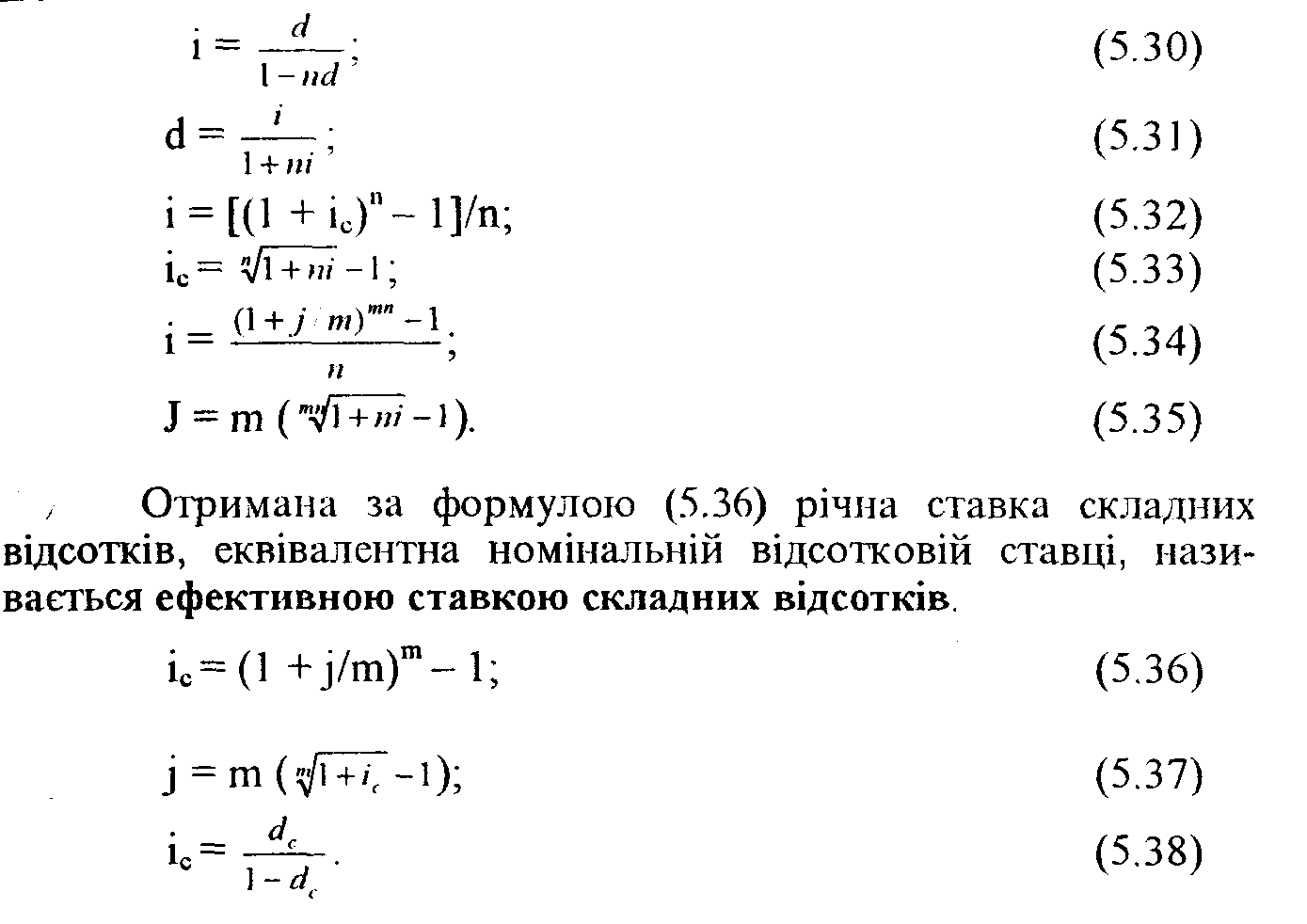
Визначення індексу інфляції. Відношення ^s/s, що виражене у відсотках, називається рівнем інфляції. При розрахунках використовують відносну величину рівня інфляції - темп інфляції - а.
Величину (1 + а), що показує, у скільки разів Sa більше за s (тобто у скільки разів у середньому виросли ціни), називають індексом інфляції іі.
Для визначення відсоткових ставок, враховуючи інфляцію, використовують формули:
197
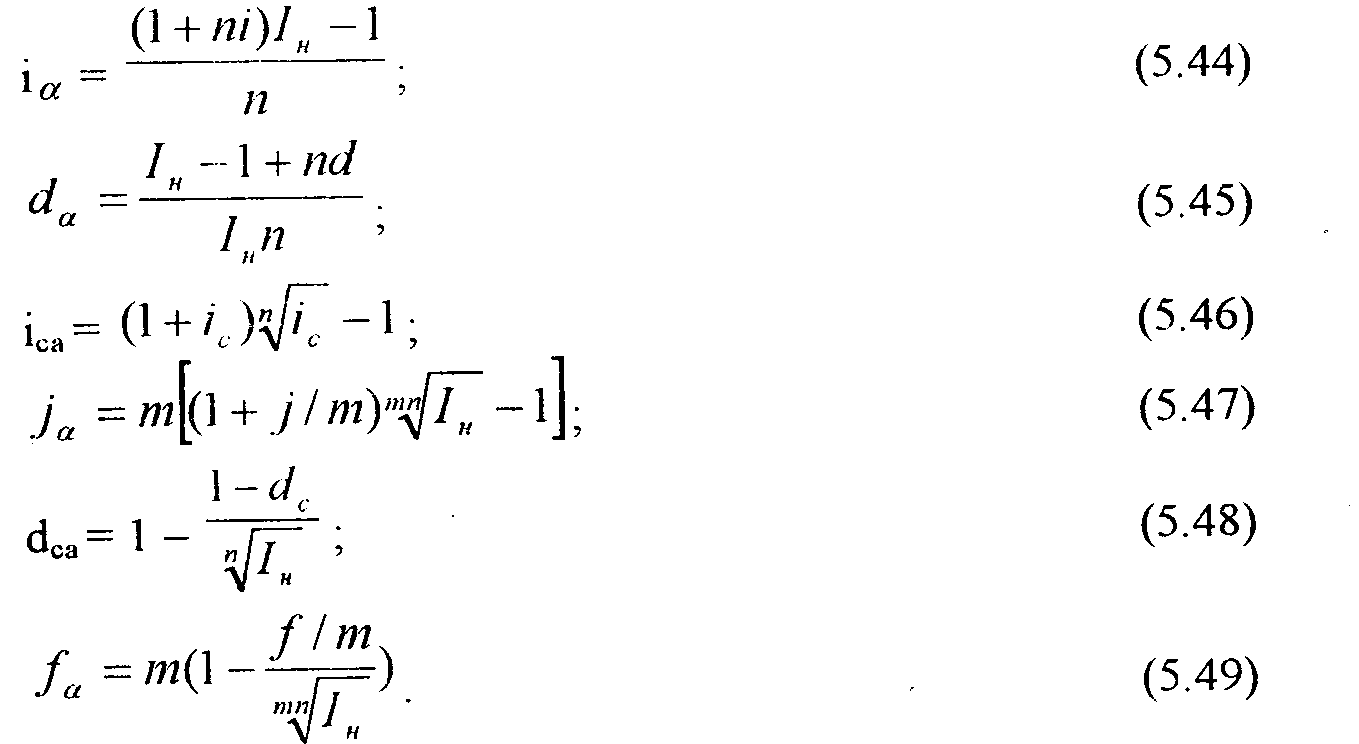
Для нарощеної суми ануїтету. При погашенні кредиту частинами поточне значення суми боргу буде після чергової сплати зменшуватись, і відповідно, буде зменшуватись сума відсотків, що нараховується на черговому інтервалі.
Розмір сплати в кінці першого року :
Si = D/n + Dg; (5.50)
D - сума кредиту;
g - річна ставка відсотків за кредитом у відносних одиницях. Залишок боргу в кінці другого року становитиме:
D2=D-D/n=D(l-l/n). (5.51) Розмір сплати в кінці другого року становитиме:
Sz = D/n + Dg = D/n + Dg (1 - 1/n). (5.52) Залишок боргу на початок третього року становитиме:
Di,D - D/n = D (1 - 2/п) і т. д. (5.53) Сума виплачених відсотків буде дорівнювати:
І = Dg + Dig + Dag + ..... + Dng = Dg (1+ 1 - 1/n + 1 - 2/п +....+
l-{(n-l)/n}. (5.54) Застосувавши до виразу в дужках формулу для суми
членів гсометричної'прогресії, отримуємо:
I=Dg [(n+l)/2]. ' (5.55) Загальна сума погашення кредиту буде дорівнювати:
S=D+I=D(l+g(n+l)/2]. (5.56) Якщо внески на погашення кредиту будуть здійснюватись
р раз на рік, сума сплачуваних відсотків, визначена аналогічно,
буде дорівнювати:
'І = [(D/p)gj [(пр +1) / 2].(5ІР7)~
Якщо умовами кредитної угоди передбачено, що кредит і відсотки за ним погашаються протягом його терміну рядом платежів за вказаною в угоді схемою, суму відсотків і загальну суму, що повинна бути погашена, можна визначити, послідовно використовуючи наведені вище формули.
Кредити можуть погашатись однаковими терміновими сплатами, що включають погашення основної суми боргу і виплату відповідної суми відсотків. Якщо відсотки за кредит нараховуються за простою ставкою, загальна їх сума І буде визначатись наведеною вище формулою (5.57).
Загальна сума витрат з погашення кредиту в розмірі D буде дорівнювати:
S=D+I, (5.58) і, відповідно, розмір однакових термінових сплат буде дорівнювати:
R = (D + І)/пр; (5,59) де n - термін кредиту в роках;
р - кількість сплат на рік.
При погашенні рівними терміновими сплатами довгострокових кредитів з нарахуванням відсотків за складною ставкою відсотків розміри термінових сплат можуть бути визначені, якщо перерахувати (перевести) суми сплат до моменту видачі кредиту, або, інакше кажучи, здійснювати їх дисконтування з використанням формули
P=S/(1 +i)n=Ska; (5-60) де kd- коефіцієнт дисконтування (приведення);
ka=l/(l+i)n. (5.61) Якщо платежі розміром R будуть здійснюватись щорічно в кінці кожного року, то їх значення, дисконтовані за складною ставкою відсотків і на початок першого року виплат, будуть Дорівнювати:
Ai=R/(l +i).
A2=R/(1 +І)2,
до цих формул ....
An=R/(l+i)n. (5.62)
Застосувавши до суми цих величин формулу для суми членів геометричної прогресії, отримуємо для сучасної (наведеної) величини суми всіх платежів наступне вираження:
t=l,
199
A=ZA,=R [1-(1+i)-n|/i, ^.u-^
t=n. Із цієї формули можна визначити розмір платежу:
R-Ai/|l-(l +i)-|. (5.64) Оскільки сума всіх платежів з погашення кредиту і нарахованих відсотків повинна бути рівною сумі кредиту D, розмір
сплат, що вносяться в кінці кожного року при ставці складних
відсотків і за формулою (5.64) буде дорівнювати:
R = D і/[1 - (1 + і)-]. (5.65) Загальна сума погашення кредиту складе:
S = nR = nD i/[l - (1 + i).n]. (5.66) А сума сплачених відсотків буде дорівнювати:
I=S-D. (5.67) Якщо рівнозначні виплати за кредитом у розмірі R будуть
вноситись р раз на рік, їх розмір, що визначається аналогічно,
складе:
R=D [(І +і)кр-1]/ |1-(1 +і)-„1. (5.68)
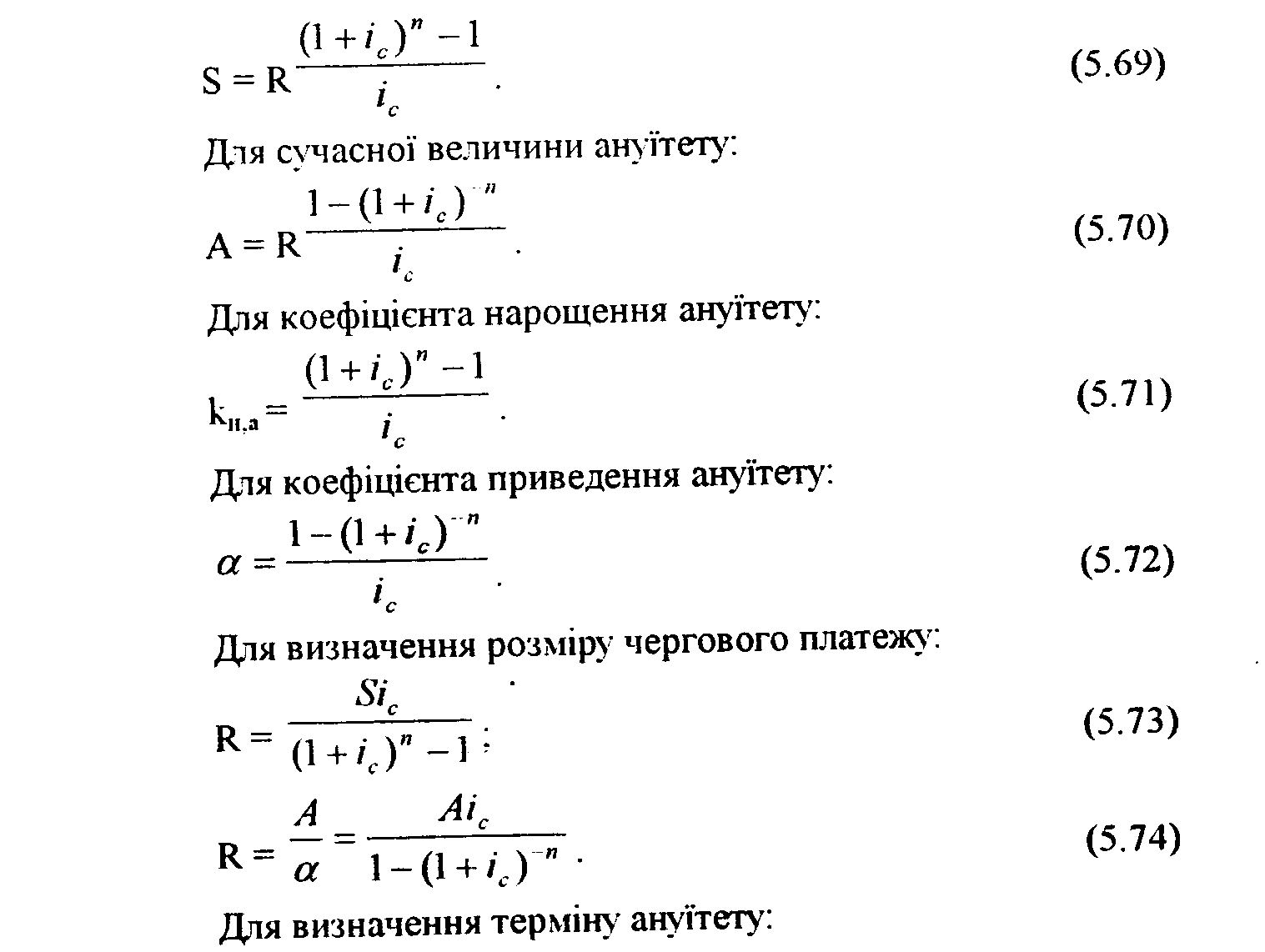
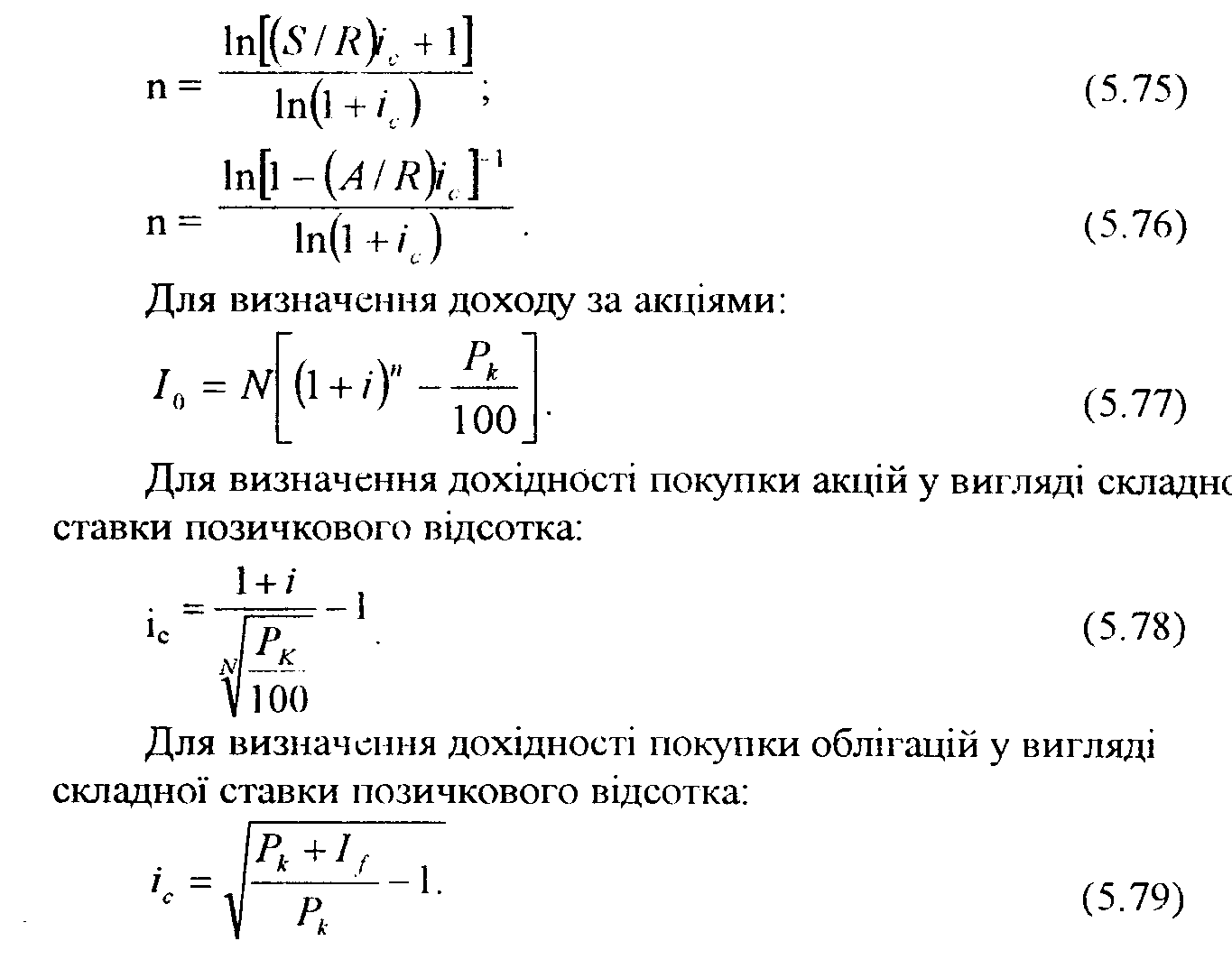
5.6.3.Способи розв'язування фінансових задач
Розв'язування фінансових задач, як і більшість інших проблем тимчасової вартості грошей, може вирішуватись трьома способами: числовим, табличним (відсоткові таблиці) або із застосуванням фінансового калькулятора.
У наш час прогрес досяг рівня, при якому більшість задач, пов'язаних з тимчасовою вартістю грошей, слід вирішувати за допомогою фінансового калькулятора. Проте необхідно розуміти концепції даної проблеми без калькулятора і знати, як будувати часові лінії для того, щоб вміти розробляти комплексні програми. Це може особливо знадобитися для розрахунку вартості цінних паперів і облігацій при проведенні лізингового аналізу, рішення інших важливих фінансових проблем.
Формат задачі. Для того, щоб розуміти різні типи задач, які стосуються тимчасової вартості грошей, ми досить часто Діємо у певному порядку: спочатку ми визначаємо дану задачу
201
Ходаківська В. II., Беляєв В. В
словами, потім подаємо її рішення за допомогою часової лінії, діаграми, далі під часовою лінією ми даємо рівняння, яке необхідно розв'язати. Розв'язати задачу можна трьома альтернативними способами, а саме:
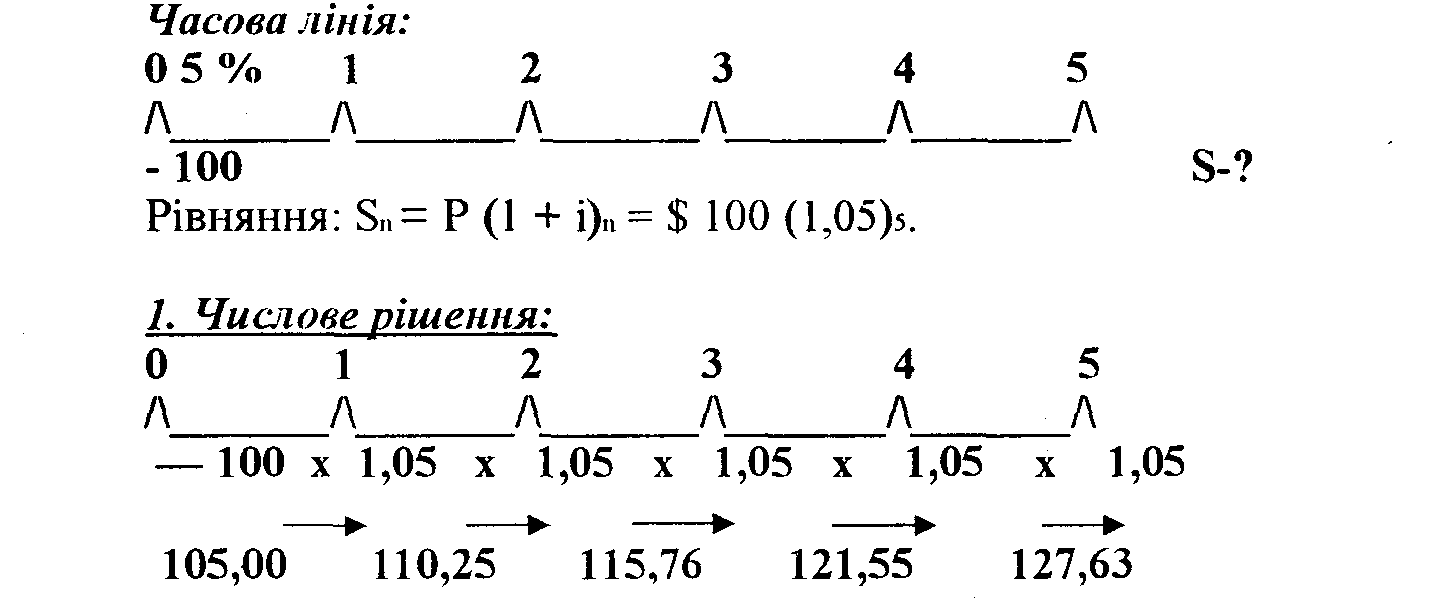
або при застосуванні звичайного калькулятора піднесіть 1.05 до 5-го ступеня і помножте на $ 100. У результаті ви отримаєте: 85 =$ 127,63.
2. Рішення за допомогою фінансових таблиць:
Фактор майбутньої вайтості відсотка k in = (1 + i)n
Г. J Г- v
|
|||
Період (n)
|
4%
|
5%
|
6%
|
1
|
1,0400
|
1.0500
|
1,0600
|
2
|
1.0816
|
1.1025
|
1.1236
|
3
|
1,1249
|
1.1576
|
1.1910
|
4
|
1,1699
|
1.2155
|
1,2625
|
5
|
1,2167
|
1.2763
|
1.3382
|
6
|
•1,2653
|
1.3401
|
1,4185
|
Знайдіть значення k 5 •/., s у таблиці, потім помножте на 100 доларів:
S5= $ 100 (k 5%,5) = $ 100 (1,2763) = $ 127,63. 3. Рішення за допомогою фінансового калькулятора:
Введені дані: Результат:
N 5,1 5, PV-100, РМТ 0, FV = 127/63 Зазначимо, що згідно з процедурою розрахунку ви повинні ввести дані тільки у заданій послідовності, а потім натиснути кнопку FV, після чого отримаєте відповідь - 127,63.
202
ринок фінансових послуг: теорія і практика
~ПИТАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ НАД ТЕМОЮ
Рівень 1.
1. Організація депозитного ринку як основа проведення активних операції! банків.
2. Операції, пов'язані із залученням грошових коштів на вклади, називаються ...
3. Існують різні ознаки класифікації вкладів. Назвіть їх.
4. Чому вклади до запитання (безстрокові депозити) в своїй основі нестабільні. що обмежує сферу їх використання комерційними банками?
5. Які два типи вкладів до запитання ви знаєте?
6. Для ефективного управління тимчасово вільною готівкою клієнта банки застосовують методи, що дозволяють мінімізувати розміри грошових коштів, що зберігаються на безпроцентних поточних рахунках. Назвіть ці методи.
7.Які вклади переважають у структурі депозитів у комерційних банках України? Чим це пояснюється?
8. Термінові вклади та їх різновидності.
9. Депозитні та ощадні сертифікати: особливості випуску та обігу.
10. Яку роль у ресурсах банків відіграють ощадні вклади населення та їх типи?
11. Охарактеризуйте механізм міжбанківських кореспондентських відносин.
12. У якому порядку та формі комерційним банкам надаються кредити центральних банків?
13. Євровалютні кредити як фінансовий інструмент управління пасивними операціями комерційних банків.
14. Тезаврація дорогоцінних металів як спосіб накопичення грошових заощаджень, тобто акумуляції капіталу.
15. Механізм здійснення банками операцій із золотом.
16. Основні види та форми грошових розрахунків.
17. Особливості здійснення готівкових розрахунків. Кредитні та де-бетні картки.
18. Із чим пов'язана організація безготівкового грошового обороту?
19. Система безготівкових розрахунків як фіорма організації руху грошей на рахунках у банку. На яких принципах вона базується?
20. Особливосгі організації обліку банками виданих клієнтам кредитів (банки відкривають їм позичкові рахунки). Назвіть основні види позичкових рахунків.
21. Перерахування г рош'ей на рахунках банку базується на двох основних принципах. Назвіть їх.
22. Виходячи із специфіки проведення безготівкових розрахунків. виділяються три рівні їх організації. Назвіть їх.
23. Міждержавні розрахунки як окрема організаційна форма, що існує в умовах грошової системи закритого типу. Охарактеризуйте механізм.
203
Ходаківська В.П., Беляєн В.В
24. Оріанізація міждержавних розрахунків у і ротовій системі відкри-
1010 Till IV.
25. Міжбанківські розрахунки u умовах однорівневої іа дворівневої банківської системи.
26. Грошові та безгрошові розрахунки юридичних та фізичних осіб. що здіііснююгься банками.
27. Особливості розрахунків за товарними і нетоварними операціями.
28. Як розрізняються розрахунки за способом оплати товарів та послу] •?
29. Залежно від кількості учасників розрахунки можуть бути прямими чи транзитними. У чому полягає між ними різниця?
30. У процесі безготівкових перерахувань клієнти банків України використовують п'ять основних форм розрахунків, які відрізняються за формою розрахункових документів та порядком документообороту. Назвіть їх.
31. Механізм здійснення розрахунків платіжними вимогами.
32. Механізм здійснення розрахунків платіжними дорученнями.
33. Особливості здійснення платежів при розрахунках чеками із чекових книжок.
34. Механізм здійснення розрахунків акредитивами.
35. В умовах розвитку ринкових відносин в Україні почали впроваджуватися платіжні вимоги-доручення - форма розрахунків, аналогічна перевідним векселям. У чому полягає сутність механізму їх здіснення?
36. Загальна класифікація інструментів грошового ринку.
37. Комерційні папери та банківські акцепти як інструменти грошового ринку.
38. Вексель як універсальний інструмент кредиту, платіжний засіб, абстрактний цінний папір.
39. Функції векселя.
40. Особливості організації вексельного ринку в Україні.
Рівень 2.
41. Вексель відповідно до Закону України "Про особливості обігу векселів в Україні" - це ...
42. Векселі бувають прості (соло-вексель) і перевідні (тратта). У чому полягає різниця між ними?
43. Відмінні особливості оформлення векселя.
44. За 4'ормою передачі векселя за індосаментом, останній може бути двох видів: або іменним, або бланковим. У чому їх особливості?
45. Які операції виконують банки з векселями?
46. Спеціальний позиковий рахунок - це ...
47. Інкасування векселів банком - це ...
48. Доміціляція (від лат. doiniciliuin - місцеперебування) векселя - це
49. Аваль (фр. aval) векселя - це ...
50. Акцепт (лат. Acceptus - прийнятий) векселя - це...
51. Місце державних фінансових інститутів на грошовому ринку.
204
Рийок фінансових послуг: теорія / практик»
52. Дія забезпечення оріаніі.іціі іотівковою і рошеного обії v Національний банк здійснює: ...
53. Основні економічні засоби іа методи грошово-кредитної політики НБУ.
54. Відкріпнії ринок • це ринок, на якому здійснюються операції •;
купівлі-продажу цінних паперів між особами, що ...
55. Операціями на відкритому ринку Національної о банку є ...
56. Назвіть критерії вибору банку вкладниками.
57. Від чого залежить ціна кредиту, якчіі отримує позичальник у банку?
58. Хто є емітентом комерційних паперів?
59. Виходячії із зюди про зворотний викуп, ви очікуватимете від них вищий чи нижчий дохід, ніж від комерційних паперів? Чому?
60. Для чого існують банківські акцепти?
61. Які види процентних ставок ви знаєте?
62. Назвіть основні фактори, які впливають на процентні ставки.
63. Що таке номінальна процентна ставка, і чим вона відрізняється від реальної?
64. Які державні цінні напери обертаються на і рошовому ринку?
65. Яким чином казначейство використовує первинний ринок для одержання капіталу?
66. Взаємозв'язок грошово-кредитної та бюджетної політики держави.
67. Концепція тимчасової вартості ірошей.
68. Особливості здійснення розрахунків на грошовому ринку в умовах інфляції.
69. Поясніть, іцо лежить в основі виразу: "Долар, який ви маєте в наявності сьогодні, дорожчий, ніж долар, який ви одержите у наступному році".
70. Що таке компаундирування?
71. Що таке дисконтування? Як цей процес співвідноситься із процесом компаундирування?
72. Як зміниться поточна вартість суми, яку ви очікуєте отримати в майбутньому, з плином часу і при підвищенні відсоткової ставки?
73. Припустимо, що ви знаєте поточну вартість вашого рахунку, суму вашого рахунку наприкінці певного року та процентну ставку. Напишіть рівняння, за допомогою якого знаходимо число періодів.
74. Припустимо, що ви знаєте поточну вартість вашого рахунку, суму вашого рахунку наприкінці певної о року та число періодів. Напишіть рівняння. ча допомогою якого ми можемо знайти процентну ставку.
75. Теперішня вартість майбутнього потоку готівки або групи потоків готівки:
а) ставка "ціни шансу";
б) дисконтування:
в) поточна вартість:
г) правильної відповіді немає.
Ходаківська В. її., Беляєв В. В
76. До відпливу грошової готівки слід віднести:
а) витрати та виплати;
6) прийняття готівки;
в) депозити готівкою;
г) інвестування.
77. До припливу грошової готівки слід віднести:
а) витрати та виплати;
б) прийняття готівки;
в) депозити готівкою;
г) інвестування.
78. Де б ви віддали перевагу зберігати кошти: 1) на ощадному рахунку. за яким виплачуються 5 відсотків при піврічному компаундируваині або: 2) на рахунку, за яким 5 відсотків компаундирується щоденно? Поясніть, чому.
79. Чому з точки зору інвестора піврічне компаунднрування краще за
річне?
80. Назвіть основні напрями вдосконалення податкового регулювання
депозитного ринку.
Рівень 3. Завдання для практичної роботи
81. Вексель на суму 32000 грн. видано на 230 днів з нарахуванням за ним відсотків за ставкою 25% річних при розрахунковій кількості днів на рік -365. Банк облікував вексель за 54 дні до настання терміну оплати за обліковою ставкою 10% річних при розрахунковій кількості днів на рік - 360. Визначити суму, отриману пред'явником векселя, і суму доходу банку.
82. При обліку векселя на суму 2300 гри., до терміну оплати якого залишилось 80 днів, банк виплатив його пред'явнику 1810 грн. Визначити, яку облікову ставку використовував банк при розрахунковій кількості днів на рік,
рівному 360.
83. При оплаті пред'явленого векселя на суму 12000 грн., до терміну
погашення якого залишилось 32 дні, дохід банку склав 2125 гри. Визначити ставку відсотків, використану банком при визначенні доходу.
84. Вексель обліковано в банку за обліковою ставкою 25% річних за сім місяців до терміну його погашення. Визначити значення ефективної річної ставки відсотків.
85. Вексель, до терміну оплати якого залишилось 150 днів, обліковано
в банку за обліковою ставкою 35% річних при розрахунковій кількості днів на рік - 360. Визначити дохідність операції обліку за ефективною ставкою простих
відсотків для розрахункової кількості днів на рік - 365.
86. Депозитний сертифікат дисконтного типу номіналом 15000 грн., ціна якого визначається з використанням облікової ставки, було куплено за півроку до його погашення і продано через 3 місяці. Значення ринкових облікових ставок у моменти купівлі та продажу склали 40% і 35% річних відповідно. Визначити дохід від операцій купівлі-продажу та її дохідність у вигляді ефективної річної ставки відсотків. 206
87. Ощадний серті^ика'і номіналом 50 000 ірн. з нарахуванням процентів за ставкою 30% річних і терміном півроку було куплено за 110 днів до погашення і продано через 15 днів. Значення ставок відсотків за депозитами в моменти купівлі та продажу склали 30% і 28% річних відповідно. Визначити дохід від операції купівлі-продажу і її дохідність у вигляді е4іективної річної ставки відсотків при розрахунковій кількості днів на рік - 360.
88. Вексель обліковується в банку за півроку до терміну його погашен-ня. Місячний рівень інфляції складає 2%. Визначити облікову ставку, яка забезпечує реальну дохідність операції обліку, що відповідає реальній дохідності кредитних операцій 6% річних.
89. При обліку векселів в умовах інфляції повинна бути забезпечена реальна дохідність, що визначається обліковою ставкою, яка дорівнює 8% річних. Визначити облікову ставку, що компенсує втрати від інфляції при обліку векселя, до терміну погашення якого залишилось 75 днів, якщо очікуваний рівень інфляції складає 3% в місяць, а розрахункова кількість днів на рік - 360.
90. Вексель на суму 20000 грн. було пред'явлено в банк для оплати за 250 днів до терміну його погашення. Визначити суму, отриману пред'явником векселя, і суму доходу банку, якщо банк для його визначення буде використовувати ставку відсотків і облікову ставку, що дорівнюють 25% річних (розрахункова кількість днів на рік при використанні ставки відсотків дорівнює 365, при використанні облікової ставки - 360).
91. Банк приймає внески до запитання за ставкою 80% річних. Визначити cvmv процентів на внесок 2400 грн., що розміщено на півроку.
92. Банк приймає депозити на 3 місяці за ставкою 20% річних, на 6 місяців за ставкою 40% річних і на рік за ставкою 50% річних. Визначити суму, яку отримає власник депозиту 4400 гри. в усіх трьох випадках.
93. Вклад у розмірі 4000 грн. було покладено в банк 20.01.02 і запитано 7.10.02. Ставка відсотків банку складала 30% річних. Визначити суму нарахованих відсотків при різних методах визначення терміну нарахування.
94. При відкритті ощадного рахунку за ставкою 25% річних 20.04.02 на рахунок було покладено суму 4000 гри. Потім на рахунок 21.07.02 була додана сума 400 гри.: 7.10.02з рахунку було знято суму 770 грн., а 11.11.02 рахунок було закрито. Визначити загальну суму. отриману вкладником при закритті рахунку.
95. Ставка відсотків банку за внесками до запитання, що складає на початку року 30% річних, через півроку була зменшена до 25%, а через три місяці До 20%. Визначити суму відсотків, яку було нараховано на вклад 4000 грн. за рік.
96. Вклад 4000 грн. було. покладено в банк 25.05.02 при ставці 35% річних. З 1 червня банк знизив ставку за внесками до 25% річних. 15 липня рахунок було закрито. Визначити суму нарахованих відсотків при англійській практиці їх нарахування.
97. У пенсійний фонд щорічно в кінці року будуть уноситись суми 56 ірн., на які будуть нараховуватись складні відсотки за ставкою 12% річних. Визначити суми, накопичені у фонді протягом: а) 10 років; б) 20 років; в) ЗО років.
207
Ходаківська В. І Е., Беляєв В. В
98. Y пенсійний фонд v кінці кожної о кварталу будуть вноситись суми 10.40 гри., на які також щоквартально будуть нараховувагись складні відсотки •за номінальною річною ставкою 11 "о річних. Визначити суми, накопичені у
фонді протягом 20 років.
99. На внески в пснсііініііі фонд. що вносяться щорічно в кінці року. будуть нараховувашсь складні відсотки за ставкою 15% річних. Визначити розмір щорічних внесків, необхідних для накопичення через 26 років суми 22000 гри.
100. Y пенсійний фонд на початку кожного кварталу будуть вноситись суми 13,40 гри., на які також щоквартально будуть нараховуватись складні відсотки за номінальною річною ставкою і 4% річних. Визначити суми, накопичені у фонді протніом 25 років.
101. У пенсійний фонд щорічно на початку кожного року будуть вноситись суми, на які будуть нараховуватись складні відсотки за ставкою 16% річних. Визначити розмір внесків, необхідних для накопичення через ЗО років
суми 48000 гри.
!02. Вексель на суму 32000 гри. видано на 230 днів з нарахуванням
відсотків за ставкою 25% річних іірі; розрахунковій кількості днів на рік - 365. Банк облікував вексель за 54 дні до г'.асгання терміну оплати за обліковою ставкою 10% річних при розрахунковії! кількості днів на рік - 360. Визначити суму,
отриману пред'явником векселя, і суму доходу банку.
і 03. При обліку векселя на суму 2300 грн.. до терміну оплати якою залишилось 80 днів. банк виплатив по; о пред'явнику 1810 ірн. Ви значити, яку облікову ставку використовував банк при ро ірахунковііі кількості днів на рік - 360.
104 При оплаті пред'явленої о векселя на суму 12000 ірн., до терміну погашення якого залищії.'юсь 32 дні. дохід банку склав 2125 гри. Визначити
ставку відсотків, використану банком при визначенні доходу.
105. Вексель обліковано в банку за обліковою ставкою 25% річних за сім місяців до терміну його иоі ащення. Визначити значення ефективної річної
ставки відсотків.
106. Банк видав кредит у розмірі 15000 гри. на 9 місяців за ставкою 35%
річних. Визначити суму, що погашається, і суму відсотків за кредит.
107. Кредит у розмірі 7500 гри. було взято 5.01.02 з іерміном погашення 11.07.02 за ставкою 30% річних. Визначити суму відсотків за кредит при
різній практиці їх нарахування.
108. За умовами кредитної угоди ставка простих відсотків у першому
місяці за користування кредитом дорівнює 45% річних, а в кожному наступному місяці збільшується на 2 відсоткових пункти. Визначити суму відсотків за
кредит у розмірі 11000 гри., взятий на 9 місяців.
109. Банк нараховує відсотки :за складною ставкою 35'- о річних. Визначити суму нарахованих відсотків, якщо вклад 4000 гри. було закрито через 3.5
року.
!ІО. Складні відсотки на вкладі! нараховуються щоквартально і'.і
номінальною ставкою 25% річних. Визначити суму відсотків, нарахованих на внесок 4000 ірн. за 4 роки.
Ринок фінансових послуг: теорія і прак'пікя
~ВАРІАНТИ ЗАВДАНЬ ДЛЯ організації ПОТОЧНОГО ТА ПІДСУМКОВОГО КОНТРОЛЮ ЗНАНЬ СТУДЕНТІВ
Варіант індивідуального контрольного завдання № 1 |
|
|
ip. Up. Шр
|
26.25.31.23.І7.32.39.13 | 75.79,70.46,74,64.50.57,54, 69
|
109.99
|
|
Варіант індивідуального хошролькоґ-озаддаірм-№ 2
|
|
1р. 11р. Шр.
|
8, 5.26. 2. li.28.24, 15
|
60.64,52,69,42,49,72.66,55,43 89,86 1
|
|
Варіант індивідуального коЕ;грольа.огс)'зав,паяня.ХйгЗ
|
|
ip. ІІр. Шр.
|
39. 6. 17.24. П. 3. 9. 12 і 78,57,79,77,44,59,71,61,47,41 100.108
|
Варіант індивідуального вгонтрольног'ав'авдання .№ 4
|
|
lp.J26.35- 4. 2. 1.1Л6. 15.20 Пр.|б3, 42, 41, 73. 69, 57, 51, 58, 55, 46 Шр.|і04,98
|
|
Варіант індивідуального контролї-ного завдання № 5 [
|
|
Ір. Up. Гір.
|
18. 7. 15.32.20.33.34.40 45.51.53.47.43.71,66.61-59. 62
|
87.91
|
|
Варіант індивідуального контрольного завда;:ня л^і б !
|
|
Ір. 1ІП. Шр.
|
35, 10, 16,24,31. 3, 7,25 | 44,49,59,66,68,7 і,72,55,80,76 83. 103
|
Варіаіп-ігіДивіду'альнЬгохотрЬїїБкУпйавданняХ"?;
|
|
Ір. Up.
|
15,33, 3, 1, 5,23,25,26 80,47,50,70,65.55.45,53,73,49
|
ПГр,
|
95.107
|
Варіант індивідуального кбнтрбдьнЙЖі'^Івяйн'в^їІ08
|
|
ip. Up. Пір.
|
24. 10. 6. 13,35. 14.28.25 68,64,54,48,42,71,44.58,72,45
|
101.86
|
|
Варіант індивідуального контрольного: Завдання №'9 .
|
|
Ір. lip. IIIp.
|
14.26.24. 8-28.23.38. 3 47,73,68,78,63,45,46,59,56,44 і 04.88
|
Варіант індивідуального контрольного заТад&іня №> 10
|
|
Ір,|26, 16,35,31, 17, 2.40, 9 Up. 57.67,48,56,73,46,68,49,78.7 і Шр, 105.106
|
|
20
|
|
Кодаківська В.П., Беляєв В. В
|
||
Вай^^ндйві^й^і^кМфба&віай^^йїї^ .11 •
|
|
|
ір. Пр. Ulp. .
|
16,17,11, 7,37,27, 15,38 49,78,66,60,71,55,68,45,42,65 94,106
|
|
Варіазд"4Вдий®АЙ^і^:йоїіїр6лбНог'б |"гі$аа&йя' № 12
|
||
Up. Шр.
|
Ір. - -37,24,15, 2,34,22, 1,13 58,70.62.49.73.59,54. 50.65, 71 106,84
|
|
Варійй.шд&взід^йЙ^їюайтролй ІЗ.,
|
||
Ір. Up. Шр. .
|
4,28,13, 12, 2,40, 10,35 42,56,66,59,51,55,78.45,79,60 105.102 і———————————,———————————————^————•g. '.. -! •.^——-^Я——Ж.-;-.111.^--,1. ..'-———•————-;——————————————————
|
|
В^анійіййЖ^йійіЙіонтрЙаІЇ^
|
||
Up. Шр. .
|
Ір. - - 17,31,37,19,39,26, 3,35 42.44,64.61,57.49.76,77,72,63 107,98
|
|
Варіант індивідуалБНбго контрблБн6тозавдїЕвї[ЯХ215
|
||
1р. Пр. Шр. .
|
11,31, 2, 7,19, 8,39, 16 72,50,44,46,48,51,59,69,49,54 92,85 ——————————————————————————————————-——————————-———. •ч і r.—i. ! ,——., „• • -. і————• „.';;".——————————————————————
|
|
Варіант івдйвідаальноФ.'коійроі&нопз-заШіюня^Ж' 16'
|
||
Ір. Пр. Шр.
|
26. 17.25.27. 15.23.38.29 75,64,63,55,71,68,78,77,48,79 101.82
|
|
Варіаіа^ййсві.йхалЙ^Й&тЕЙЖ^^ййЙжЗ^ЇЖ-;
|
||
Ір. Пр. шр.- .
|
28.20,16, 5, 1,17,22,27
|
|
55, 63, 68, 49, 47,71,60,54,48,69 96,103
|
||
ВаріанТчн)йвіЙ%й88і^&шдайЙЙ^
|
||
ip. Пр. Шр.
|
26.22, 1, 2,18,19,29.40 79.48.55.50.45.74.71.77,75.63
|
|
82,81
|
||
Варіант індивіда'альнбгб'контроі&нбго завдання № 19...
|
||
Ір. Up. Шр.
|
29,33,12. 4. 9. 18, 2,15 64,69,43,60,51,54,53,57,56,42 92.83
|
|
Варіант вддивід\'альной.контр@л^йогозавданад^^^^
|
||
Ір, пр Шр
|
7. 29 6 30 37 4. 25 21
|
|
66. 74'. 54. 48'. 72, 63. 67. 55. 76, 64 110,87
|
||
1 Ринок фінансових послуг: теорія і практик ^ ^ - . -- -.- •— • - ———
|
||
4.:.
|
В~•^•g^jaatg^^a^'TiV,,;-.^^.»'- ,.
|
|
Ір. Пр. пір.
|
9.33. 10, 13, 12, 2. 17.31
|
|
64,68,57,46,41,60,53,45,74,44
|
||
82,85
|
||
to'ft-^'^^'^^&s'.^u^^^'t^^^^.^S'^'iSi-^^^^HSi^^^^^^^^iSA^
|
||
Ір. Up. пір.
|
24.25. 12,31,33,16, 3.37
|
|
56,79,77,69,71,57,46,70.80,63
|
||
'———————^--92,81
|
||
|
||
Ір. Пр. пір. ——————
|
38,28.31,26,37,21,22. 1
|
|
76,59,71,57,47,68,75,54,53.70 100.109
|
||
[ 1
|
||
Ір. Up. пір.
|
27,11. 9,30,38,34. 8, 4-
|
|
47.43.61,42,48,75,46, 54, 66, 60
|
||
81. 110
|
||
Варіайг^^віжальйоі^.;ікбйй^^^в»е^^^^й
|
||
Ір. Up. Пір.
|
13,33,29,34, 1,38, 5, 9
|
|
71.45.60,76,65,61.48. 46, 78, 53
|
||
96.97
|
||
|
||
Ір. Up. пір.
|
30.26.23.36,40.18. 8,11 46. 55. 67.54.45,70.57.76,42,65 •
|
|
104.90
|
||
|
||
Ір. Up. Шр.
|
30,35,22,40,38.18, 4,36 77,48.55,51,54,62. 69, 42,74,46
|
|
107,85
|
||
ВарїаЙ^ЙЕЙЗДЮвЙЙЯЙЙІ^^^^И^Й^^^^
|
||
Ір. Up. IIIp.
|
1^ 01 11 1^ Л'і 1 ТЇ 00 JJ, Z.I, J 1 , 13, ij, 3, LJ, 20
|
|
46,75.79,47,53,42.49.43.64,55 90,98
|
||
ВаріанЇЗ^ЇЩальн6га-хонті»Ш5^а|давай^Ш
|
||
Ір. Up, IIIp.
|
1,38.31,33,30,23,24,35
|
|
80,52,60,77,72,53,41,79, 46, 73 93.81
|
||
Варіант •індивідуальною кбнтрЗлій'ойїйавданнйі^ЗД.»
|
||
Ір. Up, IIIp.
|
7.35.39. 2. 6,12,14,36 47 73.57,60,67,77,74.45.54.66 98.104
|
|
|
||
ВаріеіІйнІздЩлуадьногоконтрольного завдання .№'31
|
|
|
r- ip.
|
4.27. 9.20.40. ! 7. 18. 19
|
|
Пр. Шр.
|
73,47,74,53,57,76,80,72,75,52 81.97
|
|
ВаріааЙ^йвідаотіЙ'ЗДїон^ф^ 'ЗЗ.л.
|
||
1р. Up, Шр.
|
4, 6.35, 11,22,28,39,29 47.69 74.5І.60.79.68.78.55.80
|
|
107,110
|
||
Варіант їіййвід^ЧБНой^оюуойййгй'.йвдання^:^^^^
|
||
1ір' Пр.
|
33. 7.39. 10.21,30. 9. 18 49-56.45.59.74.43.71, 44. 75. 51
|
|
Шр.
|
96.109
|
|
ВаріайЯнді|ві^^ьаЬго-ісоігірбйнбгб'зав
|
||
ip. Пр. Шр.
|
15,39,31,10, 1,12,35,21 63,78,56,46,69,44,61, 50, 73, 67 89,86
|
|
Варіант індивіяуального контролвного;завдання№3&,.
|
||
ip. Пр. Шр.
|
26,39.37, 12, 14, 8,38, 7 53.58.45.78.64.59.46,66,61.57 97,82
|
|
( ТЕМА б. ФІНАНСОВІ ПОСЛУГИ НА І ВАЛЮТНОМУ РИНКУ