22, Способы преобразования чертежа. Вращение вокруг проецирующих прямых

23. Способ прямоугольного треугольника. Определение натуральной величины отрезка прямой линии и углов его наклона к плоскостям проекций

а) смотрите 20; б) Угол наклона отрезка к плоскости проекций равен углу между гипотенузой и проекцией отрезка на той же плоскости. Пример: Определить длину отрезка AB и угол его наклона b к плоскости H.

П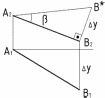 ри определении длины отрезка за катет прямоугольного треугольника может быть выбрана любая проекция отрезка. Другое дело, если определяется угол наклона отрезка к той или иной плоскости проекций. Здесь выбор падает на проекцию отрезка, принадлежащую именно той же плоскости проекций.

Решение: Строим прямоугольный треугольник, приняв за катет фронтальную проекцию отрезка A2B2. Второй катет по длине равен разности координат точек A и B в направлении мнимой в данном случае оси y. На чертеже эта разница берется на другой плоскости проекций: на плоскости V . Из построенного треугольника делаем выводы:

b= углу между A2B2 и A2B

24. Развертка цилиндрической и канонической поверхности. Геодезическая линия на поверхности.

построение развёртки поверхности можно выполнить иремя способами:

1)способом нормального сечения

2)способом раскатки

3)способом треугольника

1.способом нормального сечения

Н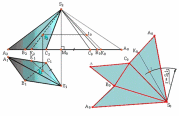 аходим натуральный вид этого сечения методом замены плоскостей проекций.

Поскольку боковые ребра призмы параллельны между собой, а стороны нормального сечения перпендикулярны к ним, на развертке призмы боковые ребра будут также параллельны, а стороны нормального сечения развернуться в одну прямую.

В этой связи для построения развертки призмы необходимо отложить на произвольной прямой М0М0 натуральные величины сторон нормального сечения, через их концы провести прямые, перпендикулярные к этой прямой. Затем следует отложить по обе стороны от прямой М0М0 отрезки боковых ребер, взятые на плоскости проекций П2, и соединить отрезками прямых концы отложенных отрезков. В результате получим развертку боковой поверхности призмы. Присоединяя к этой развертке оба основания призмы, получим ее полную развертку.

2.способом раскатки

Способ раскатки целесообразен при построении разверток в том случае, когда основания призмы параллельны какой-либо одной плоскости проекций, а ее ребра или образующие цилиндра и конуса занимают положение линий уровня.

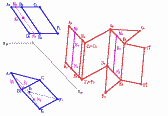
Если ребра призмы или образующие цилиндра, конуса занимают общее положение, то прежде чем приступить к построению развертки, следует с помощью известных методов преобразования чертежа перевести их в частное положение, при котором ребра или образующие будут параллельны какой-либо плоскости проекций.

Сущность способа состоит в том, что грани призмы или образующие цилиндра последовательно вращаются вокруг ребер до совмещения соответственно с фронтальной или горизонтальной плоскостью.Основание цилиндра делим на 12 равных частей и через полученные точки проводим образующие. Из точек /2, 22 122 опускаем перпендикуляры к очерковой образующей /2Л2 и радиусом, равным хорде 1±2Х (7i2 части деления окружности основания), последовательно делаем засечки на этих перпендикулярах, начиная от точки 72 (или отступив от нее на величину А).

Полученные точки /2, 2а, ..., /22 соединяем плавной кривой. Развертка верхнего основания симметрична развертке нижнего, так как сохраняется равенство длин всех образующих цилиндра.

3.способом треугольника (триангуляции)

Боковые грани любой пирамиды являются треугольниками. Для построения развертки пирамиды (рис. 9.2) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.У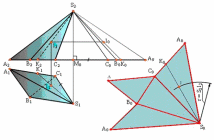 изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П1 в истинную величину. Истинные величины боковых ребер определены способом прямоугольных треугольников. S2M0C0, S2M0B0 и S2M0А0, у которых одним катетом является высота пирамиды (S2М0 - разность высот точки S и точек А, В, С), а другим - горизонтальная проекция соответствующего ребра.

(/М0C0/ = /S1C1/; /M0B0/ = /S1B1/; /M0A0/ = /S1A1/; /M0K0/ = /S1K1/).

Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П1.

Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание (АВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. Такой способ построения развертки поверхности называется способом триангуляций.

Геодезическая линия - эта линия кратчайшего расстояния между двумя точками на поверхности. На развёртке этой линии соответствует прямая. Она строится на развёртке по двум её конечным точкам , заданным на проекции предмета, а затем достраивается на заданных проекциях по дополнительным промежуточным точкам, взятым на построенной развёртке.