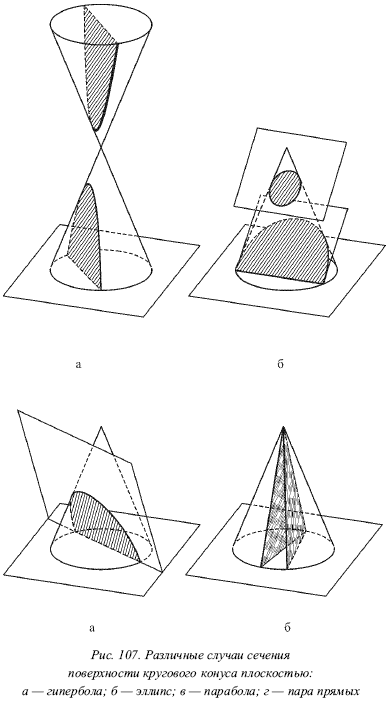
Сечение конуса вращения проецирующими плоскостями.
Характерные линии сечений прямого кругового конуса.
В зависимости от направления секущей плоскости, в сечении конуса могут получиться различные линии, называемые линиями конических вращений.
Если секущая плоскость проходит через вершину конуса, то в его сечении получается пара прямых (образующие)
Если секущая плоскость перпендикулярна к оси вращения конуса, получается окружность
Если секущая плоскость параллельная одной образующей конуса, то получается парабола
Если секущая плоскость параллельная двум образующим конуса, то получается гипербола
Если секущая плоскость пересекает все образующие конуса ( то есть не параллельна ни одной из них), то получается эллипс.
а) гипербола б) эллипс в) парабола г) пара прямых
Соосные поверхности. Метод концентрических сфер. Соосными называются геометрические тела вращения, имеющие общую ось вращения i. Поверхности соосных тел пересекаются по окружностям, перпендикулярным их общей оси. Если общая ось i соосных геометрических тел является проецирующей прямой (т.е. перпендикулярна одной плоскости проекций, а двум другим параллельна), то окружность пересечения проецируется в прямую линию, перпендикулярную их общей оси, на те плоскости проекций, которым эта общая ось параллельна. Применение способа вспомогательных концентрических сфер для построения линии пересечения поверхностей возможно при наличии трех графических условий: 1) пересекаются поверхности вращения (кроме открытого и закрытого тора); 2) общая плоскость симметрии пересекающихся поверхностей является плоскостью уровня; при этом условии точки пересечения очерков на проекции предмета, изображенного на параллельной общей плоскости симметрии плоскости проекций, принадлежат искомой линии пересечения; 3) оси поверхностей пересекаются; точка пересечения осей является центром всех вспомогательных концентрических сфер.
Сфера-посредник образует две пары соосных поверхностей с каждой из заданных поверхностей. Каждая образованная пара соосных поверхностей пересекается по соответствующим окружностям, которые проецируются в прямые, перпендикулярные общей оси каждой пары, и проходят через точки пересечения очерков каждой пары соосных поверхностей. всех вспомогательных концентрических сфер.