9. Образование поверхности. Определитель поверхности. Каркас поверхности

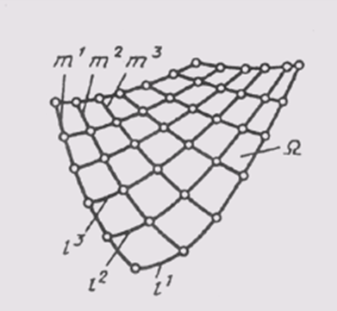
Поверхностью называют множество последовательных положений линий, перемещающихся в пространстве. Эта линия может быть прямой или кривой и называется образующей поверхности. Если образующая кривая, она может иметь постоянный или переменный вид. Перемещается образующая по направляющим, представляющим собой линии иного направления, чем образующие. Направляющие линии задают закон перемещения образующим. При перемещении образующей по направляющим создается каркас поверхности (рис. 84), представляющий собой совокупность нескольких последовательных положений образующих и направляющих. Рассматривая каркас, можно убедиться, что образующие l и направляющие т можно поменять местами, но при этом по верхность получается одна и та же.

Определител поверхности - необходимая и достаточная совокупность геометрических фигур и связей между ними, которые однозначно определяют поверхность. В число условий, входящих в состав определителя, должны быть включены. Определитель поверхности состоит из двух частей: из совокупности геометрических фигур и дополнительных сведений о характере изменения формы образующей и законе ее перемещения.

10. Образование поверхности вращения. Очерк вращения

Образование поверхности вращения. Очерк вращения

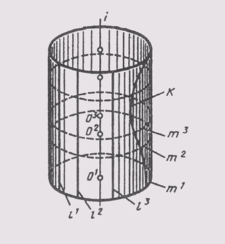
Любую поверхность вращения можно получить различными способами. Так, прямой круговой цилиндр (рис. 85) можно создать вращением образующей l вокруг оси г, ей параллельной. Тот же цилиндр образуется перемещением окружности т с центром в точке О, скользящим по оси i. Любая кривая k, лежащая на поверхности цилиндра, образует эту поверхность при своем вращении вокруг оси /'.

Очерком поверхности называются линии, которые ограничивают области ее проекций. При вращении каждая точка образующей описывает окружность, плоскость которой перпендикулярна оси.

11. Позиционные задачи. Принадлежность точки, линии поверхности. Теорема МонжаПозиционные задачи - задачи на определение общих элементов различных геометрических фигур. К ним относятся задачи на взаимную принадлежность (взять точку на линии или на поверхности, провести линию на поверхности, провести поверхность через заданные линии и т.д.) и задачи на пересечение различных геометрических объектов (найти точку пересечения линии с поверхностью или линию пересечения двух поверхностей и т.д.).

Плоскость является простейшей поверхностью, которую можно представить как веер линий, полученных при движении прямой (образующей), закрепленной в некоторой точке, по другой прямой (направляющей).

Из геометрии известны теоремы о принадлежности точки и прямой линии плоскости.

Т1. Точка принадлежит плоскости, если она принадлежит прямой линии, лежащей в плоскости.

Т2. Прямая линия принадлежит плоскости, если она проходит через 2 точки, лежащие в этой плоскости.

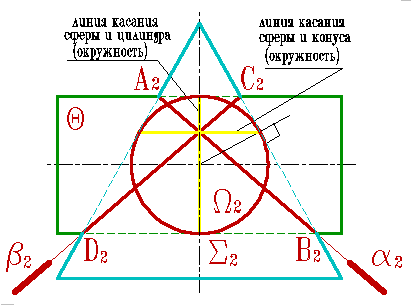
теорема Г. Монжа. Если две поверхности второго порядка описаны около третьей или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. Плоскости этих кривых проходят через прямую, соединяющую точки линий касания.

		а) модель	б) эпюр
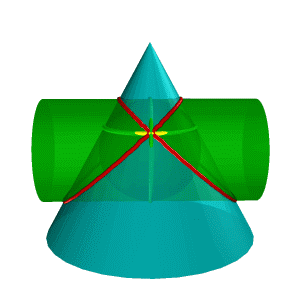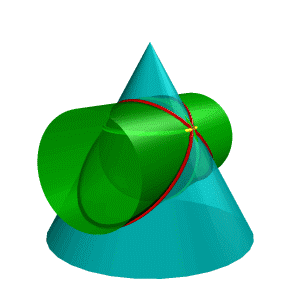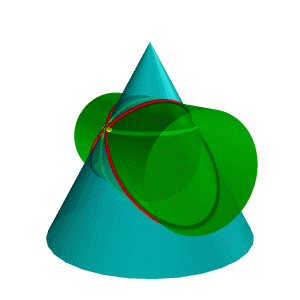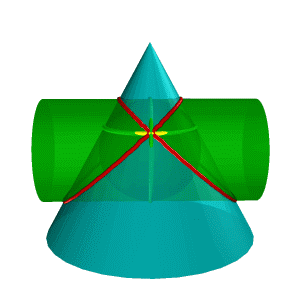
Рисунок 8.38. Пересечение конуса и цилиндра имеющих общую вписанную сферу

В соответствии с этой теоремой линия пересечения конуса Σ и цилиндра  (рис.8.38), описанных около сферы , будут плоскими кривыми – эллипсами (расположенными в плоскостях  и ), фронтальные проекции которых изображаются прямыми А₂В₂ и С₂Д₂,