
- •Билет №1.2. Правило замыкающей, правило параллелограмма сложения векторов. Свойства операции сложения вектором (с доказательством).
- •Билет №1.3. Произведение вектора на число. Свойства операции произведения вектора на число (с доказательством).
- •Билет №1.6. Свойства проекций и их величин: проекция суммы векторов, проекция произведения вектора на число, проекция линейной комбинации векторов (с доказательством).
- •Билет №1.7. Линейно зависимые, линейно независимые векторы. Критерий линейной зависимости двух векторов (с доказательством).
- •Билет №1.8. Теорема о разложении произвольного вектора плоскости по любым двум неколлинеарным векторам этой плоскости (с доказательством).
- •Билет №1.9. Критерий линейной зависимости трех векторов (с доказательством).
- •Билет №1.10. Теорема о разложении произвольного вектора плоскости по любым двум неколлинеарным векторам этой плоскости (с доказательством).
- •Билет №1. 11. Теорема о линейной зависимости любых четырех векторов (с доказательством).
- •Билет №1.14. Полярная система координат. Полюс, полярная ось. Полярный радиус, полярный угол. Главные значения полярного угла. Связь между полярными и прямоугольными координатами на плоскости.
- •Билет №1.18. Определение скалярного произведения векторов. Основные свойства скалярного произведения векторов (с доказательством).
- •Билет №1.20. Определение векторного произведения векторов. Основные свойства векторного произведения векторов (с доказательством).
- •Билет №1.21. Выражение векторного произведение векторов через координаты перемножаемых векторов (с доказательством). Двойное векторное произведение. Тождество Якоби.
- •Билет №1.22
- •Билет №1.23
- •Билет №2.1
- •Билет №2.2
- •Билет №2.3
- •Билет №2.4
- •Билет №2.5
- •Билет №2.6
- •Билет №2.7
- •Билет №2.8
- •Билет №2.9
- •Билет №2.10
- •Билет №3.2. Эксцентриситет, фокальные радиусы, фокальный параметр эллипса. Параметрические уравнения эллипса.
- •Билет №3.3. Определение гиперболы. Каноническое уравнение гиперболы (без вывода). Исследование формы. Асимптоты.
- •Билет № 3.4. Эксцентриситет, фокальные радиусы, фокальный параметр гиперболы. Директрисы эллипса и гиперболы. Свойства директрис эллипса и гиперболы.
- •Билет №3.5. Определение параболы. Каноническое уравнение параболы (с выводом). Исследование формы. Фокальный парам.
- •Б илет №3.6. Уравнение эллипса, гиперболы и параболы при вершине (с выводом). Полярное уравнение эллипса, гиперболы, параболы.
- •Билет №3.8.Понятие поверхности второго порядка. Эллипсоид, гиперболоиды, параболоиды, конус второго порядка, цилиндрические поверхности. Построение тела, ограниченного поверхностями второго порядка.
Билет №1.8. Теорема о разложении произвольного вектора плоскости по любым двум неколлинеарным векторам этой плоскости (с доказательством).
Теорема:
Если
в некоторой плоскости Π
заданы
два неколлинеарных вектора
Доказательство.
Отложим
векторы
и
от
одной точки O,
т. е. построим точки
Спроектировав
точку M
на
прямую
Д
|
Билет №1.9. Критерий линейной зависимости трех векторов (с доказательством).
Теорема: Для того чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны. Доказательство.
Пусть
векторы
,
,
Если векторы и неколлинеарны, то точки O, , определяют плоскость Π. В силу равенства отрезок такжележит в плоскости Π и, следовательно, векторы компланарны. Если векторы и коллинеарны, т. е. отрезки и лежат на одной прямой, то в силу равенства отрезок также лежит на этой прямой. Следовательно, в этом случае векторы не только компланарны, но даже и коллинеарны. Обратно, пусть векторы компланарны. Предположим сначала, что два из заданных векторов, например , , неколлинеарны. Тогда по теореме 2.4 вектор можно представить в виде , и, следовательно, векторы линейно зависимы. Пусть
теперь все три вектора (10) коллинеарны,
т. е. параллельны одной прямой. Из
теоремы 2.3 следует, например,
Переписывая
это равенство в виде
|
Билет №1.10. Теорема о разложении произвольного вектора плоскости по любым двум неколлинеарным векторам этой плоскости (с доказательством).
Теорема:
Если
векторы
,
,
Д
Пусть
,
и
Так
как векторы
|

 и
и
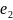 ,
то любой вектор
этой
плоскости можно разложить по векторам
,
то любой вектор
этой
плоскости можно разложить по векторам
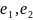 ,
т. е. представить в виде
,
т. е. представить в виде
 .
(1). Коэффициенты
.
(1). Коэффициенты
 ,
,
 определяются однозначно.
определяются однозначно.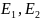 , M,
такие, что
, M,
такие, что
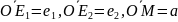
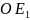 параллельно
прямой
параллельно
прямой
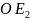 ,
получим
точку
,
получим
точку
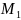 .
Пусть,
далее, точка
.
Пусть,
далее, точка
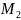 является
проекцией точки M
на
прямую
параллельно
прямой
.
Так как векторы
является
проекцией точки M
на
прямую
параллельно
прямой
.
Так как векторы
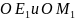 коллинеарны
и
коллинеарны
и
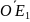 –
ненулевой
вектор, то
–
ненулевой
вектор, то
 .
Аналогично
.
Аналогично
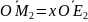 .
Так как
.
Так как
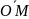 =
=
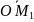 +
+
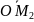 ,
то равенство (1)
верно.
,
то равенство (1)
верно.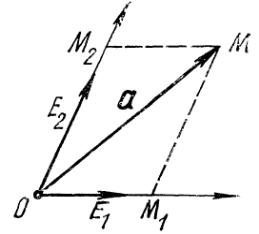 окажем
единственность разложения (1).
Пусть наряду с представлением (1)
имеется еще разложение
окажем
единственность разложения (1).
Пусть наряду с представлением (1)
имеется еще разложение
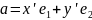 (2).
Вычитая из равенства (1)
равенство (2),
получаем
(2).
Вычитая из равенства (1)
равенство (2),
получаем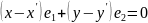 .
(3)
Так как векторы
- неколлинеарны,
то они линейно независимы, и из равенства
(3)
следует x–
x'
=
0, y–
y'
=
0 ⇒x=
x',
y=
y'.
.
(3)
Так как векторы
- неколлинеарны,
то они линейно независимы, и из равенства
(3)
следует x–
x'
=
0, y–
y'
=
0 ⇒x=
x',
y=
y'. линейно зависимы. Тогда, по крайней
мере, один из них линейно выражается
через остальные, например
линейно зависимы. Тогда, по крайней
мере, один из них линейно выражается
через остальные, например
 .Отложим
векторы
,
,
от одной точки O,
т. е.
построим такие направленные отрезки
.Отложим
векторы
,
,
от одной точки O,
т. е.
построим такие направленные отрезки
 ,
,
 и
и
 ,
что
,
что
 ,
,
 ,
,
 .
.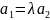 .
. ,
получаем, что векторы (10)
линейно зависимы.
,
получаем, что векторы (10)
линейно зависимы. линейно независимы, то любой вектор
может
быть разложен по этим векторам, т. е.
может быть представлен в виде
линейно независимы, то любой вектор
может
быть разложен по этим векторам, т. е.
может быть представлен в виде
 .
Это разложение единственно.
.
Это разложение единственно. оказательство:
Отложим
векторы
,
,
и
от
одной точки O,
т. е. построим такие направленные
отрезки
оказательство:
Отложим
векторы
,
,
и
от
одной точки O,
т. е. построим такие направленные
отрезки
 ,
,
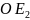 ,
,
 и
OM,
что
и
OM,
что ,
,
 ,
,
 ,
,
 .
. – проекции
точки
– проекции
точки
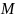 на
прямые
,
,
параллельно
плоскостям
на
прямые
,
,
параллельно
плоскостям
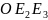 ,
,
 ,
,
 соответственно.
На отрезках
соответственно.
На отрезках
 ,
,
 ,
,
 как
на ребрах, построим параллелепипед.
Тогда
как
на ребрах, построим параллелепипед.
Тогда
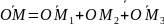 .
.
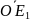 и
и
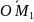 коллинеарны
и
≠
0
,
то
коллинеарны
и
≠
0
,
то
 .
Аналогично
.
Аналогично
 ,
,
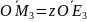 .
Единственность
разложения доказывается так же, как
и в теореме о разложении по 2-м векторам.
.
Единственность
разложения доказывается так же, как
и в теореме о разложении по 2-м векторам.