Билет №3.8.Понятие поверхности второго порядка. Эллипсоид, гиперболоиды, параболоиды, конус второго порядка, цилиндрические поверхности. Построение тела, ограниченного поверхностями второго порядка.

Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида 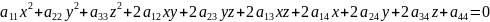, , , , , отличен от нуля.

Эллипсоид — поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением вида: 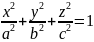. Уравнение называется каноническим уравнением эллипсоида. Величины  , ,  есть полуоси эллипсоида. Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при 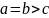  - сжатым. В случае, когда 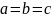 , эллипсоид представляет собой сферу.

Гиперболоид — поверхность, которая в некоторой ДПСК определяются уравнениями: , . Гиперболоид, определяемый уравнением , называется однополостным. Гиперболоид, определяемый уравнением называется двуполостным; уравнения называются каноническими уравнениями соответствующих гиперболоидов. Величины  , ,  называются полуосями гиперболоида. Гиперболоиды, определяемые уравнениями и , при   являются поверхностями вращения.

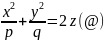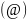Параболоид — поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями и , где   и  - положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением , называется эллиптическим; параболоид, определяемый уравнением называют гиперболическим. Уравнения и называют каноническими уравнениями соответствующих параболоидов. В случае, когда 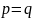 , параболоид, определяемый уравнением , является поверхностью вращения (вокруг  ).

Конус — поверхность, которая в некоторой декартовой системе координат определяется уравнением 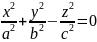, где  , 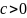, — параметры конуса.

Цилиндр —поверхность, которая в некоторой декартовой системе координат определяется уравнением, в котором не фигурирует одна из переменных: ,  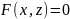или  .

Построение тела, ограниченного поверхностями второго порядка: Алгоритм построения: 1) Построить первую фигуру. 2) Построить вторую фигуру. 3) Построить поверхность их пересечения. 4) Совместить все на одном рисунке и удалить лишнее.