
- •Билет №1.2. Правило замыкающей, правило параллелограмма сложения векторов. Свойства операции сложения вектором (с доказательством).
- •Билет №1.3. Произведение вектора на число. Свойства операции произведения вектора на число (с доказательством).
- •Билет №1.6. Свойства проекций и их величин: проекция суммы векторов, проекция произведения вектора на число, проекция линейной комбинации векторов (с доказательством).
- •Билет №1.7. Линейно зависимые, линейно независимые векторы. Критерий линейной зависимости двух векторов (с доказательством).
- •Билет №1.8. Теорема о разложении произвольного вектора плоскости по любым двум неколлинеарным векторам этой плоскости (с доказательством).
- •Билет №1.9. Критерий линейной зависимости трех векторов (с доказательством).
- •Билет №1.10. Теорема о разложении произвольного вектора плоскости по любым двум неколлинеарным векторам этой плоскости (с доказательством).
- •Билет №1. 11. Теорема о линейной зависимости любых четырех векторов (с доказательством).
- •Билет №1.14. Полярная система координат. Полюс, полярная ось. Полярный радиус, полярный угол. Главные значения полярного угла. Связь между полярными и прямоугольными координатами на плоскости.
- •Билет №1.18. Определение скалярного произведения векторов. Основные свойства скалярного произведения векторов (с доказательством).
- •Билет №1.20. Определение векторного произведения векторов. Основные свойства векторного произведения векторов (с доказательством).
- •Билет №1.21. Выражение векторного произведение векторов через координаты перемножаемых векторов (с доказательством). Двойное векторное произведение. Тождество Якоби.
- •Билет №1.22
- •Билет №1.23
- •Билет №2.1
- •Билет №2.2
- •Билет №2.3
- •Билет №2.4
- •Билет №2.5
- •Билет №2.6
- •Билет №2.7
- •Билет №2.8
- •Билет №2.9
- •Билет №2.10
- •Билет №3.2. Эксцентриситет, фокальные радиусы, фокальный параметр эллипса. Параметрические уравнения эллипса.
- •Билет №3.3. Определение гиперболы. Каноническое уравнение гиперболы (без вывода). Исследование формы. Асимптоты.
- •Билет № 3.4. Эксцентриситет, фокальные радиусы, фокальный параметр гиперболы. Директрисы эллипса и гиперболы. Свойства директрис эллипса и гиперболы.
- •Билет №3.5. Определение параболы. Каноническое уравнение параболы (с выводом). Исследование формы. Фокальный парам.
- •Б илет №3.6. Уравнение эллипса, гиперболы и параболы при вершине (с выводом). Полярное уравнение эллипса, гиперболы, параболы.
- •Билет №3.8.Понятие поверхности второго порядка. Эллипсоид, гиперболоиды, параболоиды, конус второго порядка, цилиндрические поверхности. Построение тела, ограниченного поверхностями второго порядка.
Билет №2.6
Расстоянием
от точки
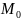 до
прямой Δназывается
длина перпендикуляра, опущенного из
точки
на
прямуюΔ.
до
прямой Δназывается
длина перпендикуляра, опущенного из
точки
на
прямуюΔ.
Возьмем некоторую прямоугольную систему координат (O, i, j) (рис.). Рассмотрим орт e, перпендикулярный прямой Δ. ЕслипрямаяΔ проходит через начало координат, то в качестве e выберем любой из двух взаимно противоположных ортов, перпендикулярных этой прямой. Если же прямаяΔ не проходит через начало координат, то в качестве e возьмем тот орт, который направлен от начала координат к прямой. Обозначим буквой α угол между векторами i и e. Тогда e (cosα, sinα). Обозначим буквой N точку пересечения прямой Δ с перпендикуляром , проведенным из начала координат к этой прямой, а буквой p – расстояние от начала координат до прямой Δ, т. е. длину отрезка ON. Т Выражая
скалярное произведение через координаты
перемножаемых векторов, получаем
Это уравнение называется нормальным уравнением прямой Δ.
|
Формулы
для отклонения и расстояния
от точки
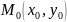 до
прямой:
до
прямой: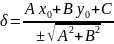 ,
,
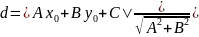 .
.
Отклонением точки от прямой Δназывается число δ, которое задается следующим образом:
Пусть d – расстояние от точки до прямой Δ.
1) δ = d, если точка лежит в положительной полуплоскости;
2) δ = –d, если точка лежит в отрицательной полуплоскости;
3) δ = d = 0, если ∈ Δ.
Геометрически
смысл
для неравенств
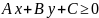 ,
,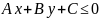 для
прямой, заданной уравнением
для
прямой, заданной уравнением
 .
.
ПрямаяΔ разбивает множество всех точек плоскости, не принадлежащих этой прямой, на два подмножества, называемых полуплоскостями. Полуплоскость, в которую направлен орт e, отложенный от точки N, назовем положительной, а вторую полуплоскость – отрицательной. Заметим, что начало координат всегда находится в отрицательной полуплоскости или лежит на прямойΔ.
Для всех точек положительной полуплоскости, определяемой прямой, неравенство принимает положительные численные значения; для всех точек второй полуплоскости неравенство имеет противоположный знак.
Билет №2.7
П В
качестве направляющих векторов этих
прямых берем векторы
Здесь буквой ϕ обозначен один из двух углов, образуемых прямыми при их пересечении. Если эти прямые не пересекаются, т. е.параллельны, то угол между ними по определению считается равным нулю. Из
формулы (16)
следует необходимое и достаточное
условие перпендикулярных прямых (14)
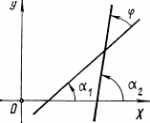
и (15): Пусть теперь прямые заданы в прямоугольной системе координат уравнениями
Обозначим
буквой ϕ
угол, на
который надо повернуть прямую
вокруг
точки пересечения этих прямых, чтобы
совместить ее с прямой
|
Пусть
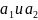 –
углы наклона
прямых
к
оси
,
т. е.
–
углы наклона
прямых
к
оси
,
т. е.
 ,
(рис).
,
(рис).
Тогда
ϕ =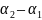 и
и (19).
(19).
Если прямые параллельны, то считаем ϕ = 0.
Если
прямые
перпендикулярные, то тангенс угла ϕ
не
существует, т. е. знаменатель в формуле
(19)
обращается ноль: .Условие
перпендикулярности прямых
.Условие
перпендикулярности прямых
 имеет
вид:
имеет
вид:
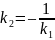 .
.

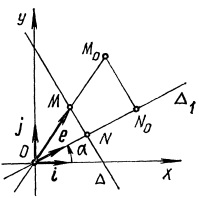 очка
M(x,
y)
принадлежит прямой Δ
тогда
и только тогда, когда ортогональная
проекция точки M
на
прямуюΔ
совпадает
с точкой N.Это
условие равносильно следующему:
очка
M(x,
y)
принадлежит прямой Δ
тогда
и только тогда, когда ортогональная
проекция точки M
на
прямуюΔ
совпадает
с точкой N.Это
условие равносильно следующему:
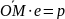 .
.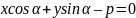 .
(12)
.
(12) усть
на плоскости заданы две прямые
своими
уравнениями относительно прямоугольной
системы координат Oxy:
(14),
(15) .
усть
на плоскости заданы две прямые
своими
уравнениями относительно прямоугольной
системы координат Oxy:
(14),
(15) .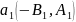 ,
,
 .
Поэтому
.
Поэтому
 .
(16)
.
(16) .
.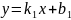 ,
(17)
,
(17)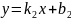 .
(18)
.
(18) .
.