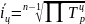18. Ряды распределения. Атрибутивный и вариационные ряды. Дискретные и интервальные ряды.

Результаты статистических сводок и группировок могут быть представлены в виде статистических рядов – упорядоченных совокупностей значений показателей (статистического признака). По своему содержанию статистические ряды подразделяются на ряды динамики и ряды распределения.

Рядом динамики называют систематизированную совокупность числовых данных, характеризующих изменения изучаемых явлений во времени.

Ряд распределения, представляет собой систематизированную последовательность статистических единиц, сгруппированных по конкретному признаку. Он характеризует состав изучаемого явления, позволяет судить об однородности совокупности, закономерности распределения статистических единиц. Обычно ряд распределения представляет собой результат структурной группировки.

Ряд распределения считается построенным, если известно, каким образом меняются в совокупности значения признака и как часто встречаются отдельные значения признака.

Для различных статистических признаков строятся ряды распределения разного типа:

• атрибутивные – строятся по описательным признакам в порядке возрастания или убывания наблюденных значений признака; примером атрибутивных рядов могут служить распределения населения по национальности, по профессиям, по полу; распределение предприятий по формам собственности;

• вариационные - строятся по количественным признакам, например, распределение рабочих по уровню квалификации, по заработной плате, распределение студентов по успеваемости.

Вариационные ряды делятся на дискретные и интервальные.

В дискретных рядах признак принимает только целые значения, например, размер семьи, тарифный разряд.

Интервальные ряды основаны на непрерывных признаках, принимающих любые, в том числе и дробные значения

Основными элементами рядов распределения являются:

1) значения признака (варианты):

• χ _i - дискретное в дискретных рядах;

• χ _i ^н- χ _i^в - интервал для интервальных рядов.

2) частота n _i - число единиц совокупности, обладающих данным значением признака. Частота показывает, сколько раз данное значение признака встречается в совокупности; сумма всех частот всегда равна объему статистической совокупности.

19. Статистика национального богатства: основные понятия и категории. Состав и структура НБ.

Основным составным элементом совокупного экономического потенциала национальной экономики является национальное богатство. Его объем во многом определяет масштабы и темпы экономического роста, что делает актуальной его оценку как одного из показателей функционирования национальной экономики.

НБ – это совокупность накопленных материальных благ, являющихся плодом человеческого труда, земли, природных ресурсов, находящихся в чьей-либо собственности, а так же невоспроизводимых и финансовых активов.

Оно состоит из экономических объектов, собственники которых получают экономическую выгоду.

В состав национального богатства национального богатства включаются нефинансовые и финансовые активы.

Произведенные нефинансовые активы создаются в результате производственных процессов и включают три основных элемента: основные фонды (основной капитал), запасы материальных оборотных средств и ценности.

Финансовые активы:

- наличность, депозиты в банках, вклады, чеки, страховые полисы, вложения в ценные бумаги;

- портфельные вложения в акции предприятий;

- пакеты акций других предприятий, дающие право контроля;

- паи или долевые участия в предприятиях.

В настоящее время российская статистика оценивает только три составляющих НБ: основные фонды, материальные оборотные средства и накопленное домашнее имущество.

Основные фонды – многократное использование в процессе производства, срок использования превышает 12 мес.; материальные оборотные средства – оборотные фонды, включающие производственные запасы (сырье, топливо) и товарно-материальные ценности (готовая продукция); накопленное домашнее имущество (потребительский капитал) – предметы личного потребления со сроком службы более 1 года.

На практике для подсчета национального богатства используются элементы СНС. Это позволяет определить его примерный объем, но при этом не требует серьезных материальных и финансовых затрат. Для этого используется такая составляющая СНС, как совокупность институциональных единиц по секторам.

20. Расчет общих индексов и определение влияния факторов на стоимостные прироста продукции.?

21. Виды средних величин и формулы их расчета. Значение структурных средних.

Средним называется обобщающий показатель статистической совокупности, характеризующий наиболее типичный уровень явления. Он выражает величину признака, отнесённую к единице совокупности. Особенности средних показателей заключаются в том, что они, во-первых, отражают то общее, что присуще всем единицам совокупности; во-вторых, в них взаимопогашаются те отклонения значений признака, которые возникают под воздействием случайных факторов. Это означает, что средний показатель отражает типичный уровень признака, формирующийся под воздействием основных доминирующих неслучайных факторов.

Средняя арифметическая используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности.

При этом если индивидуальные значения признака у статистических единиц заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.

Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле: , N – объем совокупности, x_i – количественное значение данного признака.

Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным или вариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднюю сгруппированных величин:

f_i – частота появления изучаемого признака.

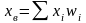, ,w – доля значения признака, принадлежащего объекту i в общем числе единиц совокупности.

Среднее арифметическое взвешенное по интервальному ряду (найти середину ряда, применить формулу).

Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когда статистическая информация не содержит частот по отдельным значениям признака, а представлена произведением значения признака на частоту.

Если исходные данные несгруппированны, то применяется средняя гармоническая простая: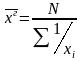

Для сгруппированных: 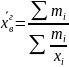, где m_i=x_if_i – взвешенная оценка признака.

22. Роль доходов в СНС. Показатели доходов.?

23. Задачи и система показателей статистики национального богатства.

Статистика национального богатства призвана решать следующие задачи:

четкое определение экономического содержания национального богатства, компонентов, входящих в его состав, и их границ;

подготовка соответствующих классификаций по различным признакам (формам собственности, натурально-вещественному составу, отраслям и секторам экономики и др.);

выработка единых методологических принципов оценки конкретных элементов богатства: земли, природных ресурсов, нематериальных активов и т. д.;

разработка необходимой информационной базы для отражения объема, структуры и динамики национального богатства и его отдельных элементов;

разработка и утверждение статистического инструментария для наблюдения за элементами национального богатства;

взаимоувязка рассчитываемых показателей национального богатства с другими обобщающими показателями (валовым внутренним продуктом, национальным доходом, национальным сбережением и накоплением и т. д.);

разработка методологии расчета производных показателей для экономико-статистического анализа роли элементов национального богатства в развитии экономики страны.

Система показателей статистики национального богатства

Национальное богатство как показатель используется для характеристики имущественного положения страны. Как комплексная экономическая категория, национальное богатство характеризуется системой статистических показателей. В ней выделяются следующие подсистемы показателей:

объема национального богатства в целом и его компонентов;

состава и структуры НБ;

состояния отдельных компонентов НБ;

простого и расширенного воспроизводства национального богатства и его компонентов;

использования НБ;

эффективности использования НБ;

динамики национального богатства.

Показатели национального богатства по основным элементам (всего и на душу населения) служат одной из важнейших характеристик достигнутого страной уровня социально-экономического развития.

24. План статистического наблюдения. Программа наблюдения. – В № 9

26. Основные категории статистики.

Статистика изучает свой предмет при помощи определенных категорий, то есть понятий, отражающих наиболее общие и существенные свойства, признаки, связи и отношения предметов и явлений объективного мира.

В статистике таких основных понятий - пять:

Статистическая совокупность – множество существующих во времени и пространстве варьирующих явлений, однокачественных (однородных) по определенному признаку. Это может быть совокупность жителей Санкт-Петербурга, совокупность студентов ИТМО, и т.д.

Статистическая единица – неразложимый первичный независимый элемент статистической совокупности, являющийся носителем определённого статистического признака. Она является пределом дробления статистической совокупности, при котором сохраняются все свойства изучаемого явления или процесса, ее частным случаем. Выбор статистической единицы определяется целью и уровнем проводимого статистического исследования. Например, можно изучать производительность труда на уровне отрасли, предприятия, цеха, участка, бригады. В каждом случае статистические единицы будут разными: предприятие отрасли, работник данного предприятия, рабочий данного цеха, бригады.

Статистический признак – характерное свойство, определённое качество статистической совокупности. Например, статистическими признаками предприятий могут являться: форма собственности, численность работающих, величина уставного капитала, стоимость активов и т. д. Значение признака отдельной единицы статистической совокупности называется вариантой.

Статистическая закономерность. Как философская категория любая закономерность есть форма проявления причинной связи, выражающаяся в последовательности, регулярности, повторяемости событий с высокой степенью вероятности, если причины, порождающие события не меняются или меняются не значительно.

Статистическая закономерность – это объективная количественная закономерность изменения массовых явлений и процессов, то есть статистическая закономерность является количественной формой проявления причинной связи. Она устанавливается на основе анализа массовых данных и проявляется только на уровне статистической совокупности. Закономерность возникает как результат воздействия большого числа постоянно действующих причин и причин случайных, действующих временами. Постоянно действующие причины придают изменениям в явлениях регулярность и повторяемость, случайные – вызывают отклонения в этой регулярности. На уровне статистических единиц закономерность проявляется не всегда; например, известно, что средняя продолжительность жизни у женщин больше, чем у мужчин. Но это не означает, что каждая женщина живёт дольше, чем каждый мужчина (среди мужчин встречается больше долгожителей).

Статистические показатели являются одной из важнейших категорий статистики, они используются для описания исследуемых массовых явлений и процессов, являются инструментом их познания.

Как философская категория статистический показатель есть мера, т.е. единство качественного и количественного отражения свойств объективных явлений и процессов в научном познании.

Статистический показатель есть количественно-качественная обобщающая характеристика какого-либо свойства статистической совокупности в условиях конкретного места и времени. Этим он отличается от индивидуальных значений признака (вариант). Например, средняя заработная плата работников предприятия – статистический показатель, а заработная плата конкретного работника – это индивидуальное значение признака (варианта).

В отличие от индивидуального значения признака статистический показатель может быть получен только расчетным путем.

В соответствии с определением статистический показатель имеет определенную структуру, в нем различают качественную и количественную стороны. Качественная сторона статистического показателя определяется признаком, который подлежит изучению и отражается в названии показателя, количественная сторона - в численном значении показателя.

Еще одной особенностью статистических показателей является то, что они всегда привязаны к конкретным обстоятельствам места и времени.

Классификация статистических показателей

Выполняемая функция: плановые, учётные, прогностические;

Охватываемые единицы совокупности: индивидуальные, сводные;

Форма выражения: абсолютные, относительные, средние.

Плановые показатели - отражают директивную функцию, ориентированы на выполнение поставленных задач, учётные – показывают реальное состояние изучаемого явления, а прогностические – его возможное состояние в будущем.

Индивидуальные – характеризуют отдельный объект или отдельную единицу совокупности – предприятие, домохозяйство и др. Примером индивидуальных статистических показателей может быть объем продаж торговой фирмы, численность работающих предприятия и т.д.

Сводные (обобщающие) показатели исчисляются по всей совокупности в целом, являются научными абстракциями и занимают особое место в познании статистических закономерностей.

Абсолютные – количественное значение объекта, явления, процесса в определенный момент времени или за определенный период.

Относительные – производные, вторичные показатели по отношению к абсолютным, выражающие определённые соотношения между количественными характеристиками статистических совокупностей.

Средние – наиболее распространённая форма статистических показателей, характеризующая наиболее типичный уровень явления. Рассчитываются на единицу статистической совокупности или на единицу признака.

27. Типологические таблицы: место и роль в статистическом анализе.?

28. Система счетов в СНС.?

29. Сводка и группировка материалов статистического наблюдения.

Сводка материалов наблюдения представляет собой комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность, с целью обнаружения типичных черт и закономерностей, присущих изучаемому явлению в целом.

Статистическая сводка (простая сводка) в узком смысле слова представляет собой операцию по подсчету общих итоговых (суммарных) данных по совокупности единиц наблюдения. Статистическая сводка (сложная сводка) в широком смысле слова включает в себя также группировку данных наблюдения, подсчет общих и групповых итогов, получение системы взаимосвязанных показателей,

представление результатов группировки и сводки в виде статистических таблиц.

Задача сводки – дать характеристику объекту исследования с помощью систем статистических показателей, выявить и измерить таким путем его существенные черты и особенности. Эта задача решается на трех этапах:

• определение групп и подгрупп;

• определение системы показателей;

• определение видов таблиц.

На первом этапе осуществляется систематизация, группировка материалов, собранных при наблюдении. На втором этапе уточняется предусмотренная планом система показателей, с помощью которых количественно характеризуются свойства и особенности изучаемого предмета. На третьем этапе исчисляются сами показатели, и обобщенные данные для наглядности и удобства представляются в таблицах, статистических рядах, графиках, диаграммах.

Перечисленные этапы сводки еще до начала ее проведения отражаются в специально составляемой программе. Программа статистической сводки содержит перечень групп, на которые целесообразно разделить совокупность, их границы в соответствии с группировочными признаками; систему показателей, характеризующих совокупность, и методику их расчета; систему макетов разработочных таблиц, в которых будут представлены итоги расчетов.

Наряду с программой существует план проведения сводки, который предусматривает ее организацию. План проведения сводки должен содержать указания о последовательности и сроках выполнения ее отдельных частей, об ответственных за ее выполнение, порядке изложения результатов, а также предусматривать координацию работы всех организаций, задействованных в ее проведении.

Статистические группировки – первый этап статистической сводки, позволяющий выделить из массы исходного статистического материала однородные группы единиц, обладающих общим сходством в качественном и количественном отношениях. Важно понимать, что группировка – это не субъективный технический прием разделения совокупности на части, а научно обоснованный процесс разделения множества единиц совокупности по определенному признаку.

На основе применения метода группировок определяются группы по принципу подобия и различия единиц совокупности. Подобие – это однородность единиц в определенных пределах (группах); различие – это их существенное расхождение по группам.

Итак, группировка – разделение общей совокупности единиц по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в качественном и количественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности или проанализировать связи между отдельными признаками. Основными задачами, решаемыми с помощью группировок, в статистике являются следующие:

• выделение в совокупности изучаемых явлений их социально-экономических типов;

• изучение структуры общественных явлений;

• выявление связей и зависимостей между общественными явлениями.

Виды: Типологическая – разделение разнородной совокупности на на однокачественные группы; структурной группировкой предназначена для изучения совокупности по какому-либо варьирующему признаку. К структурным группировкам относятся группировка населения по полу, возрасту, уровню образования, группировка предприятий по численности работников, уровню заработной платы, объему работ и т. д. Аналитическая группировка – средство изучения связи между признаками.

35. Добавленная стоимость: методы расчета и значения ВДС.?

40. Способы расчета аналитических показателей рядов динамики. Метод разностей, темп роста, темп прироста.

Ряд динамики (временной ряд) – совокупность (последовательность) количественных значений какого-либо признака за определенный период времени или в определенные моменты времени. Может быть моментным (конкретная дата) и интервальным (промежуток времени – год).

Базисные показатели – значения текущего периода сравниваются со значением периода, имеющим первое место во временном ряду (базисом).

Цепные показатели – значение показателя сравнивают со значением показателя, предшествующего периода.

Абсолютный прирост Δ характеризует размер увеличения (уменьшения) уровня ряда по сравнению с выбранной базой:

• цепной абсолютный прирост показывает, на сколько изменилось значение данного уровня по сравнению с предыдущим, то есть приращение уровня по сравнению с предыдущим:

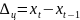
• базисный абсолютный прирост показывает, на сколько изменилось значение данного уровня по сравнению с исходным (начальным) уровне

Коэффициент роста характеризует интенсивность изменения уровней ряда (скорость изменения уровней). Он показывает, во сколько раз уровень данного периода выше или ниже базисного уровня. Этот показатель как относительная величина, выраженная в долях единицы, называется коэффициентом (индексом) роста; выраженная в процентах, называется темпом роста.

• Цепной коэффициент роста показывает, во сколько раз текущий уровень выше или ниже предыдущего: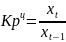

• Базисный коэффициент роста показывает, во сколько раз текущий уровень выше или ниже начального уровня:

Темп роста:

Темп прироста: ; Т^б_пр=*** ; Т_пр=К_пр*100%; Т_пр=Т_р-100.

Средние показатели ряда динамики.

Средний уровень ряда – простая арифметическая средняя.

Для моментного ряда:

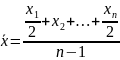
Среднее абсолютное изменение уровней ряда: = ;

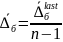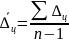Среднее относительное изменение: ;