Непрерывность элементарных функций

Разумеется, имеется бесконечно много разных функций. Однако среди них выделяется класс элементарных функций. К ним относятся:

а) степенная функция у=xⁿ;

б) показательная функция у=a^x;

в) логарифмическая функция у=log_a(x);

г) гиперболические функции sh(x), ch(x), th(x);

д) тригонометрические функции sin(x), cos(x), tg(x);

е) обратные тригонометрические функции arc sin(x), arc cos(x), arc tg(x).

Всевозможные суперпозиции этих функций также называются элементарными.

37.

Производная суммы и разности

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

1. (f + g)’ = f ’ + g ’

2. (f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.

38.

(f · g) ’ = f ’ · g + f · g ’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

Частного: Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:

39.

Производная сложной функции

Сложная функция — это не обязательно формула длиной в полкилометра. Например, достаточно взять функцию f(x) = sin x и заменить переменную x, скажем, на x² + ln x. Получится f(x) = sin (x² + ln x) — это и есть сложная функция. У нее тоже есть производная, однако найти ее по правилам, рассмотренным выше, не получится.

Как быть? В таких случаях помогает замена переменной и формула производной сложной функции:

f ’(x) = f ’(t) · t ’, если x заменяется на t(x).

Как правило, с пониманием этой формулы дело обстоит еще более печально, чем с производной частного. Поэтому ее тоже лучше объяснить на конкретных примерах, с подробным описанием каждого шага.

Пусть   -- непрерывная функция, монотонная на интервале  . Тогда, как мы доказали в гл. 3, функция   имеет обратную функцию  , которая также является непрерывной и монотонной функцией на интервале  , в который функция   переводит интервал  . Пусть   -- фиксированная точка и   -- точка, ей соответствующая. Тогда  .

40. Дифференциал функции

Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства:  где α – бесконечно малая в окрестности   функция. Для приближенного вычисления значения функции f в точке x₀ + Δx эту бесконечно малую функцию можно отбросить: 

Линейную функцию   называют дифференциалом функции f в точке   и обозначают df. Для функции x производная в каждой точке   равна 1, то есть   Поэтому пишут: 

Приближенное значение функции вблизи точки   равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом: 

Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.

Модель 3.3. Дифференциал функции.

Инвариантность формы первого дифференциала

Если x - независимая переменная, то dx = x - x₀ (фиксированное приращение). В этом случае имеем

df(x₀) = f'(x₀)dx.     (3)

Если x = φ(t) - дифференцируемая функция, то dx = φ'(t₀)dt. Следовательно,

т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.

41. Формулу

задающую определение дифференциала, можно записать в виде приближённого равенства

если считать (при малых   ) значение бесконечно малой величины   много меньшим, чем   . Перенося   в правую часть, получаем:

где   . С учётом выражения дифференциала через частные производные, находим, что

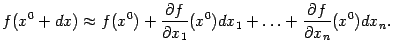
Эту формулу можно применять для приближённого вычисления значений функции   в точках   , если известны значения   и её частных производных   в точке   .

42.