24. Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.

Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.

Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности   такой, что   сходящейся к числу a, соответствующая последовательность значений функции  сходится к числу A.

25. Первым замечательным пределом называется предел

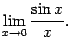
26. Определение непрерывности функции

  Пусть функция f (x) определена в некоторой окрестности точки х₀. Функция f (x) называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т. е.

                     (5.1)

или

(   ε > 0 ) (   δ = δ (ε, x₀) > 0 ) (  | x - x₀ | < δ ) : | f ( x ) − f ( x₀) | < ε

  Заметим, что в этом случае окрестность точки х₀ не является выколотой, в отличие от определения предела. Напомним, что δ – окрестностью точки х₀ называют множество всех точек х, удалённых от точки х₀ на расстояние, меньшее чем δ. Для непрерывности функции в точке требуется выполнение двух условий: существование предела функции в данной точке и совпадение этого предела с тем значением, которое функция принимает в этой точке. Так как  , то соотношение (5.1) можно записать в следующем виде:

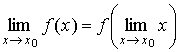
т. е. для непрерывной функции можно переставить знак функции и знак предела. Если функция непрерывна в точке х₀, то она определенна в этой точке, т.е. существует f (x₀). Заметим, что при определении предела функции в точке х₀ этого не требовалось.   Приведем еще одно определение непрерывности функции, которое по существу является перефразировкой данного определения непрерывности функции в данной точке. Если

то функция непрерывна в этой точке. Это определение вытекает из свойства предельного перехода функции в данной точке.   Приведем еще одно определение непрерывности функции, которое является перефразированной первого определения непрерывности. Перенесем в равенстве (5.1) f (x₀) под знак предела. Так как условие х → х₀ и (х − х₀) → 0 равносильны, то получаем

                     (5.2)

  Разность Δx = x - x₀ называется приращением аргумента х в точке x₀, разность Δy = f (x) − f (x₀) называется приращением функции в точке х₀, вызванным приращением аргумента Δх (рис. 5.13). При фиксированной точке х₀ величина Δу является функцией аргумента Δ х. Равенство (5.2) в новых обозначениях принимает вид

                     (5.3)

(5.3) является свойством непрерывной функции, которое можно сформулировать так: функция f (x) является непрерывной в точке х₀, если ее приращение в этой точке является бесконечно малой функцией при Δх → 0.

Арифметические действия над непрерывными функциями

  Пусть функции f (x) и g (x) непрерывны в точке х₀. Тогда функции f (x) ± g (x), f (x)·g (x) и f (x) : g (x) также непрерывны в этой точке (в последнем случае предполагается g (х₀) ≠ 0).

27. Непрерывность сложной функции

  Пусть функция у = φ (x) непрерывна в точке х₀, а функция f (y) непрерывна в точке у₀ = φ (x₀), тогда сложная функция f(φ(x)) непрерывна в точке х₀.   Доказательство. Выберем произвольную как угодно малую окрестность U(z₀) точки z₀ = f (y₀). Тогда в силу непрерывности функции f (y) найдётся такая окрестность V(y₀) точки у₀, что, если у  V(y₀), то значения функции f (y)   U(z₀). Далее, для полученной окрестности V(y₀) в силу непрерывности функции у = φ (x) в точке х₀ существует такая окрестность W(x₀), что если х   W(x₀), то значения функции у = φ(x)  V(y₀). Следовательно, для произвольной точки х   W(x₀) следует z = f (φ(x))  U(z₀). Что и требовалось доказать.   Это можно записать ещё и так

.

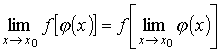Указанное выше свойство можно сформулировать в виде правила замены переменной: пусть функция у = φ (x) непрерывна в точке х₀, а функция f (y) непрерывна в точке у₀ = φ(x₀), тогда

Определение.Пусть имеется функция f(x) определенная на отрезке <a,b>, значения которой принадлежат некоторому отрезку <c,d>. Если

 ,

то говорят, что на отрезке <c,d> определена функция, обратная к функции f(x) и обозначают это так:x=f^(-1)(y).