16.Смеси идеальных газов и их свойства. Определение состава смеси.

Смесь идеальных газов представляет собой механическую смесь отдельных газов, не вступающих между собой в химические реакции. Полагаем, что от­дельные газы и смесь в целом под­чиняются уравнению состояния Клапей­рона — Менделеева. Содержание компонентов смеси обыч­но задается массовыми или объемными долями (чаще всего в процентах). Массовой долей называется отно­шение массы i-го газа, входящего в смесь, к массе смеси: . Масса смеси из п компонентов , а сумма их массовых долей .

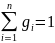Объемная доля — отношение приве­денного объема i-го газа к общему объ­ему смеси:

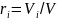
Под приведенным объемом понима­ется такой объем, который занимал бы газ при температуре и давлении смеси и при отсутствии других газов.

Смесь идеальных газов подчиняется законам поведения идеальных газов (законам Авогадро, Клапейрона, Бойля— Мариотта и т. д.). Учитывая это обстоятельство, определим соотношение между массовыми и объемными долями. Формула перехода от массовых долей к объемным и наоборот имеет следую­щий вид:

определе­нии газовой постоянной R и средней молярной массы смеси идеальных га­зов .

В смеси идеальных газов каждый i-й газ ведет себя так, как и при отсут­ствии других газов, т. е. равномерно заполняет весь объем V. Запишем урав­нение Клапейрона для i-го газа: где — парциальное давление.

17.Закон Дальтoна. Парциальное давление.

Под парциальным давлением пони­мается такое давление, которое оказал бы газ, входящий в состав смеси, если бы он находился один в том же объеме V и при той же температуре Т, что и в смеси. Закон Дальтона: каждый отдельный газ ведет себя в газовой смеси так, как будто бы он один при температуре смеси занимает весь объем.

По закону Дальтона давление смеси газов, в которой нет химических реакций между компонентами, равно сумме парциальных давлений отдельных газов: .

Просуммируем левую и правую части уравнения : ИЛИ Уравнение Клапейрона для смеси имеет вид pv=mRT.

Приравнивая правые части уравнений, найдем газовую постоянную смеси Газовая постоянная смеси газов рав­на сумме произведений массовых долей отдельных газов, на их газовую по­стоянную. Универсальная газовая постоянная , откуда средняя молярная масса газовой смеси (можно расписать R) где — молярная масса i-го компо­нента.

Используя формулы перехода получим: и .

Средняя молярная масса является условной величиной, под которой пони­мается молярная масса некоторого од­нородного газа такой же массы, что и у изучаемой смеси, и тождественного по своим физическим свойствам данной смеси.

18.Газовая постоянная и средняя молярная масса смеси.

Газовая постоянная (R) – одна из основных физических постоянных, входит в уравнение состояния 1 моля идеального газа: pV = RT, где р – давление, V – объем моля газа, Т – абсолютная температура. Газовая постоянная численно равна работе расширения 1 моля идеального газа под постоянным давлением при нагревании на 1 K.

R = pV/T = 1.01•105•22.4•10-3/273[Па•м3/моль]/K =8.31(44) Dж/(моль•K)

Уравнение для нахождения удельной газовой постоянной смеси:

R = еgiRi= 8314,2(g1/ M1+ g2/ M2+… + gn/ Mn)

Зная молярную массу смеси, можно найти газовую постоянную смеси:

R = 8,314 / M.

Зная объемный состав смеси, получим следующие формулы:

gi= (R / Ri),

еgi = Rе(ri / Ri) = 1.

Формула для вычисления удельной газовой постоянной примет вид:

R= 1 / е(ri/Ri) = 1 / (r1/ R1 + R2+… + rn / Rn).

Средняя молярная масса смеси газов является достаточно условной величиной:

M = 8314,2 / R,

M= 8314,2 / (g1R1+ g2R2 +. + gnRn).

Если произвести замену удельных газовых постоянных R1, R2,…, Rn их значениями из уравнения Клайперона, найдем среднюю молярную массу смеси газов, если смесь определяется массовыми долями:

M= 1 / (r1/ M1+ r2/ M2+. + rn/ Mn).

В случае, когда смесь определяется объемными долями, получаем следующее выражение:

R= 1 / еriRi = 8314,2 / еriMi.

Зная, что R = 8314,2 / M, получим:

M= еriMi = r1M1 + r2M2 +. + rnMn.

Таким образом, средняя молярная масса смеси газов определяется суммой произведений объемных долей на молярные массы отдельных газов, из которых состоит смесь.