Случайная величина

Одним из важнейших основных понятий теории вероятностей является понятие о случайной величине.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Примеры случайных величин:

1) число попаданий при трех выстрелах; 0, 1, 2, 3

2) число вызовов, поступавших на телефонную станцию за сутки; 1,2, 3, 4

3) частота попадания при 10 выстрелах. 0; 0,1; 0,2; …; 1,0

Во всех трех приведенных примерах случайные величины могут принимать отдельные, изолированные значения, которые можно заранее перечислить.

Такие случайные величины, принимающие только отделенные друг от друга значения, которые можно заранее перечислить, называются прерывными или дискретными случайными величинами.

Существуют случайные величины другого типа, например:

1) абсцисса точки попадания при выстреле;

2) ошибка взвешивания тела на аналитических весах;

3) скорость летательного аппарата в момент выхода на заданную высоту;

4) вес наугад взятого зерна пшеницы.

Возможные значения таких случайных величин не отделены друг от друга; они непрерывно заполняют некоторый промежуток, который иногда имеет резко выраженные границы, а чаще – границы неопределенные, расплывчатые.

Такие случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток, называются непрерывными случайными величинами.

Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая» теория вероятностей оперировала по преимуществу с событиями, то современная теория вероятностей предпочитает, где только возможно, оперировать со случайными величинами.

Функция распределения случайной величины. Её свойства

Каждая случайная величина полностью определяется своей функцией распределения.

Если x .- случайная величина, то функция F(x) = Fx (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x.

Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют простораспределением.

Функция распределения любой случайной величины обладает следующими свойствами:

F(x) определена на всей числовой прямой R;

F(x) не убывает, т.е. если x1 x2, то F(x1)  F(x2);

F(- )=0, F(+ )=1, т.е.   и  ;

F(x) непрерывна справа, т.е. 

Законы распределения дискретной случайной величины

1). Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность  , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону   можно назвать числом появле­нии события в n независимых опытах.

2). Пуассоновский закон распределения. Случайная велbчина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m со­ответствует вероятность  ,где   - некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.

3). Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответ­ствует вероятность P(X=m)=P = .  Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей Mбракованных изделий.

ЛОКАЛЬНАЯ ТЕОРЕМА МУАВРА - ЛАПЛАСА

И ФОРМУЛА ПУАССОНА

Локальная теорема Муавра — Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточ­но велико, то вероятность того, что в n независимых испытаниях событие А наступит m раз, приближенно равна:

.

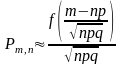где функция f(x) определяется равенством:

.

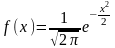Формула называется формулой Муавра — Лапласа. С воз­растанием n относительная точность значений вероятностей, по­лучаемых по ней, возрастает. В этом и заключается содержание ло­кальной теоремы Муавра — Лапласа.

ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА — ЛАПЛАСА

Интегральная теорема Муавра – Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях собы­тие А состоится число раз, заключенное в границах от а до b включительно (а < b), приближенно равна:

,

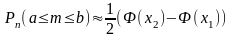где функция Ф (х) определяется равенством

,

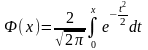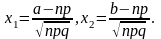
Формула называется интегральной формулой Муавра— Лапласа. Получаемые по интегральной и локальной формулам Муа­вра — Лапласа вероятности достаточно точны, если произведение nр составляет несколько сотен. В задачах, не требующих большой точ­ности ответа, можно пользоваться этими формулами и в случаях, ког­да произведение np имеет небольшое значение, однако не меньшее 20.

Мода и медиана непрерывной случайной величины

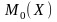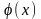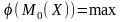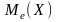Модой непрерывной случайной величины X называется такое ее значение , при котором плотность распределения имеет максимум, т. е. . Медианой непрерывной случайной величины X (обозначение: ) называется такое ее значение 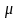, для которого одинаково вероятно, окажется ли случайная величина 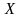меньше или больше , т. е.

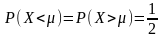
Закон больших чисел

Закон больших чисел – совокупность теорем, определяющих условия

стремления средних арифметических значений случайных величин к некоторой константе при проведении большого числа опытов.

Неравенство Чебышева. Для любой случайной величины X с

математическим ожиданием mX и дисперсией DX выполняют следующее

неравенство:

где ε > 0.

Доказательство. Рассмотрим вероятность p(/X/ ≥ε):

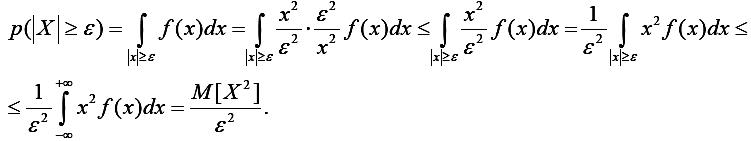
Таким образом, Заменив нецентрированную

величину X на центрированную , получим

Теорема Чебышева. Пусть произведены n одинаковых независимых

опытов, в каждом из которых случайная величина X приняла значения X1,