
- •Тема 6. Использование смешанных стратегий как способ снижения риска.
- •§1. Понятие смешанной стратегии.
- •§2. Ожидаемый доход и риск при смешанной стратегии.
- •§2.1. Ожидаемый доход смешанной стратегии.
- •§2.2. Риск смешанной стратегии.
- •§2.3. Снижение риска в смешанных стратегиях.
- •§2.4. Применение диверсификационной модели к формированию инвестиционного портфеля.
§2.4. Применение диверсификационной модели к формированию инвестиционного портфеля.
2.4.1. Понятие инвестиционного портфеля.
Инвестиционным портфелем (портфелем инвестора) называется набор ценных бумаг, находящихся в собственности участника рынка.
Ценные бумаги являются источниками дохода в виде дивидендов и капитализации (роста их стоимости).
Однако, стоимость каждого вида ценных бумаг складывается под действием множества случайных факторов и подвержена большим колебаниям.
Следовательно, инвестор рискует, вкладывая свои средства в покупку ценных бумаг. Инвестору приходится заключать компромисс между стремлением к прибыли и стремлением уклониться от риска.
2.4.2. Модель инвестиционного портфеля.
Пусть в начальный момент времени t=0 инвестор покупает различные ценные бумаги на некоторую сумму p, рассчитывая, что в момент t=1 эти же ценные бумаги будут стоить сумму p’.
Разность (p’–
p)
составляет доход инвестора, а относительная
величина
![]() (27) - доходность инвестиционного
портфеля.
(27) - доходность инвестиционного
портфеля.
Очевидно, что p’ – СВ;
dp – СВ;
p=const.
В портфель инвестора входят бумаги различных типов 1, 2, …, i, …, n, на которые он тратит средства p1, p2, …, pi, …, pn.
Причем,
![]() .
.
Разделим обе части
на p:
![]() .
.
![]() - доля инвестиций
в ценные бумаги вида i.
- доля инвестиций
в ценные бумаги вида i.
.
В момент времени t=1 ценная бумага вида i принесет доход pi’(i=1,2,…,n). Очевидно, что pi’ – СВ.
Весь доход p’:
![]() (28)
(28)
![]() (29)
(29)
В левой части: - доходность портфеля.
В правой части:
![]() - доходность ценной бумаги вида i;
- доходность ценной бумаги вида i;
- доля ценных бумаг вида i в портфеле инвестора.
Таким образом, получаем следующую формулу:
![]() (30)
(30)
С точки зрения теории риска набор чисел x1, x2, …, xi, …, xn представляет собой смешанную стратегию.
Предположим, что доходности d1, d2, …, dn – СВ с известными математическими ожиданиями m1, m2, …, mn и среднеквадратическими отклонениями σ1, σ2, …, σn.
По формулам предшествующих параграфов найдем среднюю ожидаемую доходность и риск инвестиционного портфеля.
![]() (31)
(31)
![]() (32)
(32)
где Кij – коэффициент корреляции между доходностью di и dj.
Уравнение (32) можно выразить с помощью коэффициента ковариации:
![]() (33)
(33)
Пользуясь уравнениями (31)-(33) можно ставить и решать задачи формирования портфеля инвестора с заданными свойствами.
Например, портфель, который обеспечивает определенный доход при минимальном риске, или портфель, риск которого не превышает заданной величины.
2.4.3. Портфель заданной средней доходности и минимального риска (портфель Марковица).
При заданных значениях m1, m2, …, mn – средние доходности ценных бумаг каждого вида и известных значениях σ1, σ2, …, σn – СКО, а также при известных значениях коэффициента корреляции Кij (i=1,…,n; j=1,…n).
Требуется найти
такие величины x1,
x2,
…, xn
(доли ценных бумаг каждого вида в портфеле
инвестора), которые обеспечивали бы
среднюю доходность портфеля
![]() (заданное число) при минимальном риске
(заданное число) при минимальном риске
![]() .
.
Пользуясь формулами (31)-(33), мы формулируем задачу о портфеле Марковица как задачу квадратического программирования.
Найти x1,
x2,
…, xn,
для которых целевая функция
![]() принимает
минимальное значение при следующих
ограничениях:
принимает
минимальное значение при следующих
ограничениях:

Ограничение
![]() может быть снято, какие-то значения xi
могут быть < 0.
может быть снято, какие-то значения xi
могут быть < 0.
Это возможно в том случае, когда инвестору доступна финансовая операция “short sale”.
Пусть x1 < 0 (например, x1=-0,3). А весь портфель в момент времени t=0 инвестор собирается покупать за p=100000.
Он покупает ценные бумаги первого типа в объеме:
-0,3*100000=-30000.
Т.е. фактически: продает.
“Short sale”: в момент времени t=0 инвестор заключает договор с другим лицом. Получаем сумму (-x1*p), т.е. +30000. А в момент времени t=1 он должен выплатить контрагенту доход p’=(-x1)*p’. Т.е. 0,3*p’ (в эту сумму включаются также дивиденды за этот период). Дополнительные деньги, полученные в момент t=0, инвестор направляет на покупку других ценных бумаг.
2.4.4. Портфель Тобина.
Портфель Тобина – это портфель минимального риска с использованием безрисковых активов.
Постановка задачи.
Пусть на рынке есть безрисковые ценные бумаги. С некоторой натяжкой такими можно считать государственные облигации (государственные ценные бумаги).
Инвестор распределяет свой капитал (равный единице) между безрисковыми активами и рисковыми активами.
Доля инвестиций в безрисковые активы – x0, тогда как доля в рисковые активы – (1- x0).
Рисковые активы состоят из ценных бумаг различного вида. Будем считать, что этих бумаг n: 1, 2, …, i, …, n. Обозначим долю каждой рисковой ценной бумаги как xi (i=1…n).
Тогда справедливо тождество:
![]() (1)
(1)
Обозначим: m0 – доходность безрисковых ценных бумаг;
mi – доходность рисковой ценной бумаги вида i;
mp – доходность всего портфеля.
Тогда очевидно тождество:
![]() (2)
(2)
Задача заключается
в том, чтобы найти такие числа {x1,
x2,
…, xn},
для которых риск портфеля будет
минимальным (σp![]() min)
при условии, что доходность принимает
заданные значения (mp=const).
min)
при условии, что доходность принимает
заданные значения (mp=const).
Для формализации задачи обозначим: Vij (i=1…n; j=1…n) – коэффициент ковариации ценных бумаг вида i и j.
Очевидно,
![]() .
.
Будем также считать, что безрисковые ценные бумаги абсолютно не коррелированны с остальными.
Найдем дисперсию (вариацию) рисковой части портфеля Vr:
![]() (3)
(3)
Найдем дисперсию (вариацию) всего портфеля Vp:
![]() (4)
(4)
![]()
Найдем риск портфеля rp:
![]()
![]() (5)
(5)
Уравнения (2)-(5) позволяют нам формализовать задачу Тобина в следующем виде:
![]() (6)
(6)
при условиях:
 (7)-(8)
(7)-(8)
Без вывода запишем решение задачи Тобина. Для этого введем следующие обозначения:
 - вектор-столбец,
элементами которого являются доли
рисковых ценных бумаг;
- вектор-столбец,
элементами которого являются доли
рисковых ценных бумаг;
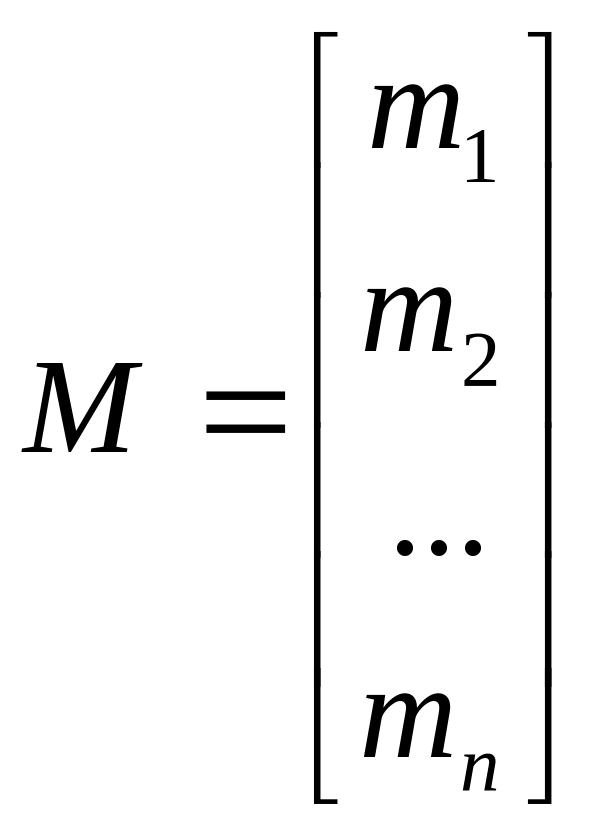 - вектор-столбец,
элементами которого являются доходности
рисковых ценных бумаг;
- вектор-столбец,
элементами которого являются доходности
рисковых ценных бумаг;
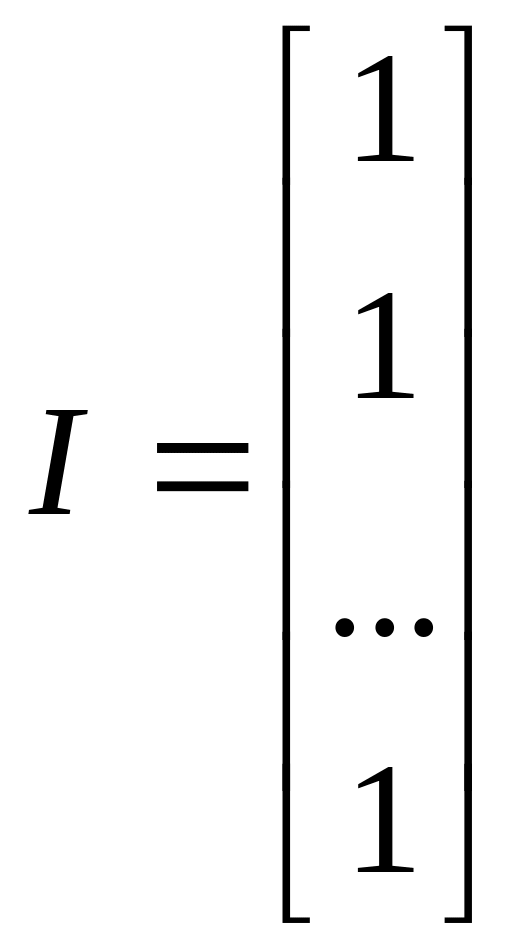 - вспомогательный
вектор.
- вспомогательный
вектор.
Тогда матричная
величина
 .
.
Введем матрицу
ковариаций (размером n![]() n):
n):
![]() - матрица является
симметричной, т.к.
- матрица является
симметричной, т.к.
![]() .
.
Поэтому транспонированная матрица будет совпадать с исходной:
![]()
Введем матрицу:
V-1
– обратная матрица ковариации. Она
также симметричная (![]() ).
).
Тобин доказал, что решением задачи (6)-(8) является вектор-столбец X*, удовлетворяющий уравнению:
![]() (9)
(9)
Покажем, что выражение в знаменателе формулы (9) является числом:
![]() - матричный столбец
n
1;
- матричный столбец
n
1;
![]() - n
n;
- n
n;
![]() - 1
n.
- 1
n.
Первое действие:
![]()
Второе действие:
![]() число.
число.
Обозначим число в знаменателе как d2:
![]() (10)
(10)
![]() (11)
(11)
- n n
- n 1 матрица n 1 (матрица-столбец).
Элементы матрицы-столбца не зависят от доходности портфеля mp. Все равно, что доходность 10, что доходность 40.
Элементы вектора-столбца определяют долю ценных бумаг каждого вида в рисковой части портфеля.
Коэффициент
![]() показывает доли этих бумаг во всем
портфеле. Эта доля прямо пропорциональна
разности
показывает доли этих бумаг во всем
портфеле. Эта доля прямо пропорциональна
разности
![]() и обратно пропорциональна d2.
и обратно пропорциональна d2.
Найдем минимальный риск портфеля Тобина. Для этого уравнение (6) запишем в матричном виде:
![]() (12)
(12)
Теперь в формулу (12) подставим X=X* из уравнения (11):
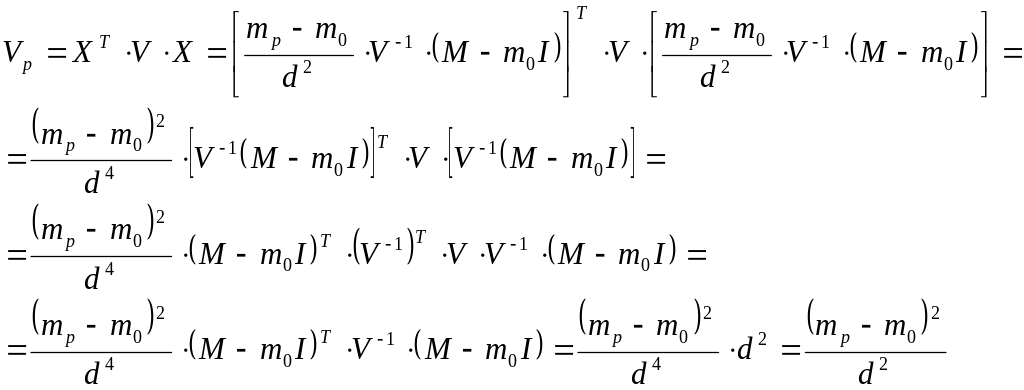
Итак, вариация всего портфеля будет равна:
![]() (13)
(13)
Отсюда находим минимальный риск портфеля:
![]() (14)
(14)
Из формулы (14) следует:
![]() (15)
(15)
В портфеле Тобина доходность является линейной функцией от риска.
2.4.5. Портфели Марковица и Тобина максимальной доходности.
Использование коэффициента ковариации ценных бумаг в портфеле инвестора позволяет ставить две взаимообратные задачи оптимальности:
нахождение портфеля минимального риска при заданной доходности;
нахождение портфеля максимальной доходности при заданном значении риска.
Будем ставить вторую задачу. Существует два варианта:
нет безрисковых бумаг – портфель Марковица;
есть безрисковые бумаги – портфель Тобина.
Портфель Марковица максимальной доходности.
![]()
при условиях:

Портфель Тобина максимальной доходности.
![]()
при условиях:
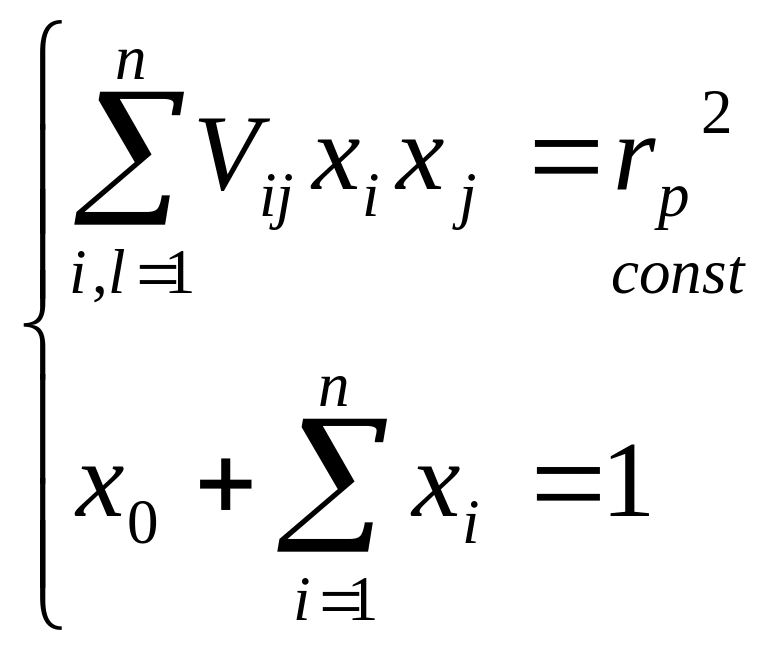
Найдем решение задачи Тобина. Для этого запишем условия в матричной форме.
![]() (1)
(1)
при условиях:
![]() (2)-(3)
(2)-(3)
Задачу (1)-(3) оптимизации будем решать с помощью функции Лагранжа (две управляемые переменные: x0 и X; два условия: λ1 и λ2).
![]()
Найдем частные производные функции Ф по переменным x0 и X:
![]() (4)-(5)
(4)-(5)
Из уравнения (4)
выразим
![]() и подставим в уравнение (5):
и подставим в уравнение (5):
![]()
![]() (6)
(6)
