Тема 6. Использование смешанных стратегий как способ снижения риска.

§1. Понятие смешанной стратегии.

В качестве метода снижения рисков хозяйствующие субъекты принимают диверсификацию.

В узком смысле диверсификация означает снижение инвестиционного риска с помощью приобретения широкого ряда ценных бумаг так, чтобы снижение курса одних из них покрывалось поднятием курса других.

В более широком смысле диверсификация – это метод, направленный на снижение риска путем распределения ресурсов между различными направлениями так, чтобы возможные потери одного направления покрывались возможными выгодами другого направления.

Если выбор одной бумаги определенного вида или выбор определенного направления расходования ресурсов отождествлять с определенной стратегией, то диверсификация будет представлять собой смешанную стратегию.

Из теории игр мы знаем, что применение смешанных стратегий позволяет достичь гарантированного результата.

Теперь выясним, как применение смешанных стратегий изменяет ожидаемый доход и риск в случае известных вероятностей состояния среды.

Будем считать, что каждая стратегия под номером I вместе со случайными факторами внешней среды приводит к тому, что доход (или полезность) ЛПР является случайной величиной (СВ) Y_i, распределенной по некоторому закону.

Обозначим:

(1)

1. – математическое ожидание дохода при выборе стратегии i;

(2)

2. – дисперсия дохода при выборе стратегии i.

Риск мы оцениваем как среднеквадратическое отклонение (СКО):

(3)

Смешанной стратегией будем называть симплекс (псевдовектор) , где , (i=1,2,…n).

(4)

Смысл величин x_i может быть различным:

1. x_i – вероятность того, что ЛПР применит стратегию i. Тогда смешанная стратегия называется вероятностной смесью.

2. x_i – относительная частота применения стратегии i. Тогда смешанная стратегия называется статистической смесью.

3. Пусть ЛПР владеет некоторым ресурсом (или капиталом) в объеме К. перед ним стоит задача распределить его между различными направлениями хозяйственной деятельности.

Обозначим к1 – часть капитала, расходуемая на первое направление;

к2 – часть капитала, расходуемая на второе направление;

… .

. Поделим на к≠0.

(5)

Обозначим - доля всего капитала, которая пойдет на направление i. (доля стратегии под № i)

Смешанная стратегия называется физической смесью.

Проблема заключается в определении смешанной стратегии, которая гарантировала бы определенный средний доход и снижала бы риск.

§2. Ожидаемый доход и риск при смешанной стратегии.

Пусть ЛПР применяет смешанную стратегию {x₁, x₂, …, x_n}. Для каждой чистой стратегии i (i=1, 2, …, n) известны средний ожидаемый доход и риск .

Требуется найти ожидаемый доход и риск при смешанной стратегии.

§2.1. Ожидаемый доход смешанной стратегии.

Обозначим Y – ожидаемый доход смешанной стратегии;

Y_i – ожидаемый доход от i-той стратегии.

Смешанную стратегию можно представить в виде таблицы:

Доли (вероятности)	x1	x2	…	xn
Доход	Y1	Y2	…	Yn

Отсюда следует, что ожидаемый доход от смешанной стратегии будет представлять собой СВ

(6)

M[Y] – средний ожидаемый доход от смешанной стратегии.

Для нахождения этой величины воспользуемся формулой из теории вероятностей: 1) ;

2) .

Найдем средний ожидаемый доход:

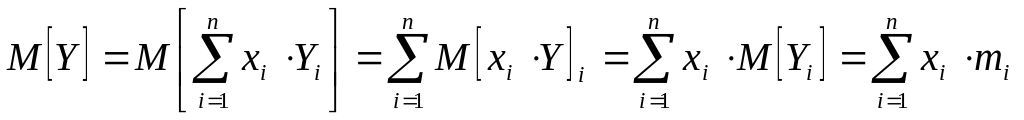
Таким образом, (7)

где M[Y] – математическое ожидание дохода при применении смешанной стратегии (средний ожидаемый доход);

m_i=M[Y_i] – математическое ожидание дохода при применении смешанной стратегии (средний ожидаемый доход i-той стратегии);

x_i – частота (доля) применения i-той стратегии в смешанной стратегии.

ВОПРОС. Можно ли увеличить средний ожидаемый доход с помощью смешанной стратегии?

Рассмотрим ожидаемые доходы для каждой чистой стратегии m₁, m₂, …, m_n и выберем наибольший из них.

Т.е., справедливо неравенство .

Средний ожидаемый доход от смешанной стратегии найдем по формуле (7): .

Т.к. x_i ≥ 0 и m_i ≤ m_k, то будет справедливо неравенство:

Таким образом, мы получили неравенство:

(8)

Средний ожидаемый доход от смешанной стратегии не превышает наибольшего значения средних доходов от чистых стратегий.

ОТВЕТ. с помощью смешанной стратегии нельзя увеличить средний ожидаемый доход.