Вопросы для самоконтроля

1. Изобразите схематически графики функций: y = sin x, y = cos x, y = tg x, y = ctg x

2. Запишите в общем виде решение уравнения sin x = a. Приведите примеры решения таких уравнений.

3. Приведите такой же анализ решения уравнений: cos x = a, tg x = a, ctg x =a.

2.4 Методы решения тригонометрических уравнений

Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения.

Разложение на множители

Пример. Решить уравнение: cos 2x – cos 8x + cos 6x = 1

Решение. cos 2x + cos 6x = 1 + cos 8x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

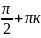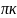4х = 3х= х=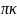

х= + к х=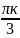

Приведение к однородному уравнению

Уравнение называется однородным относительно sin x и cos x, если все его члены одной и той же степени относительно sin x и cos x одного и того же угла.

Чтобы решить однородное уравнение, надо:

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos x в старшей степени;

д) решить полученное алгебраическое уравнение относительно tg x .

Пример. Решить уравнение: 3sin²x + 4 sinx · cosx + 5 cos²x = 2.

Решение. 3sin ² x + 4 sin x · cos x + 5 cos ² x = 2sin ² x + 2cos ²x ,

sin² x + 4 sin x · cos x + 3 cos ² x = 0 ,

tg² x + 4 tg x + 3 = 0 , отсюда y² + 4y +3 = 0 ,

корни этого уравнения: y₁ = -1, y₂ = -3, отсюда

1) tgx = –1, 2) tgx = –3,

х = - +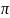 к, к€Z х = - arctg 3 + к, к€Z

3. Показательная и логарифмическая функции

Цель: студенты должны изучить определения, свойства показательной и логарифмической функций, научиться решать показательные и логарифмические уравнения и неравенства

Показательная функция y = ax, где a>0, a≠ 1

Свойства показательной функции.

Определение. Функция, заданная формулой у=а^х (гдеа>0, а≠1), называется показательной функцией с основанием а. Пусть a — неотрицательное число, x — рациональное число: . Тогда определяется по следующим правилам.

• Если x> 0, то .

• 

• 

• 

• 

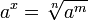Задания для самостоятельной работы

1. Укажите промежуток, которому принадлежит корень уравнения

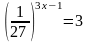
1) [-4;0) 2) [0;1) 3) [1;4) 4) [4;6)

2. Укажите промежуток, которому принадлежит корень уравнения

1) [-5;-3) 2) [-3;0] 3) (2;4] 4) (0;2]

3. Укажите промежуток, которому принадлежит корень уравнения

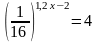
1) (-1;0] 2) (0;1] 3) (1;2] 4) (2;3]

4.Укажите промежуток, которому принадлежит корень уравнения

1) (4;0] 2) (0;1] 3) (1;3) 4) [3;6)

5. Укажите промежуток, которому принадлежит корень уравнения

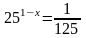
1(1;2) 2) [2;5) 3) [-2;-1] 4) (-1;1]

6. Укажите промежуток, которому принадлежит корень уравнения

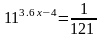
1) [-3;-1) 2) [-1;0) 3) [0;1) 4) [1;5]

7. Укажите промежуток, которому принадлежит корень уравнения

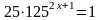
1) (5;6] 2) [-1;0) 3) [0;2] 4) (-5;-1)

8. Укажите промежуток, которому принадлежит корень уравнения

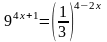
1) [-1;0) 2) [0;1) 3) [1;3) 4) [3;5]