
- •Содержание
- •Введение
- •1 Линейные уравнения, системы линейных уравнений
- •Линейные уравнения
- •1.2 Системы линейных уравнений и способы их решения
- •1.3 Определители второго порядка
- •1.4 Определители третьего порядка
- •1.5 Решение систем трех уравнений
- •Основные тригонометрические тождества.
- •Формулы сложения аргументов
- •Тригонометрические функции удвоенного аргумента
- •Простейшие тригонометрические уравнения
- •Вопросы для самоконтроля
- •2.4 Методы решения тригонометрических уравнений
- •Разложение на множители
- •Приведение к однородному уравнению
- •Показательная и логарифмическая функции
- •Показательные уравнения и неравенства Показательные уравнения, приводимые к квадратным.
- •Задания для самостоятельной работы
- •Логарифмы и их свойства
- •3.4 Логарифмические уравнения и неравенства
- •4 Векторы
- •4.1 Декартова система координат
- •4.2Векторы на плоскости и в пространстве
- •4.3 Действия над векторами
- •Задания для самостоятельной работы
- •Вопросы для самоконтроля
- •5 Прямые и плоскости в пространстве
- •5.1 Прямые на плоскости
- •5.2 Прямые и плоскости в пространстве
- •Тема для реферата
- •6 Многогранники и тела вращения
- •6.1 Призма
- •Параллелепипед
- •Задания для самостоятельной работы
- •6.2 Пирамида
- •Задания для самостоятельной работы
- •6.3Цилиндр
- •Задания для самостоятельной работы
- •6.4 Конус Задачи для самостоятельной работы
- •6.5 Шар и сфера
- •7 Предел функции
- •7.1 Раскрытие неопределенностей вида
- •7.2 Раскрытие неопределенностей вида
- •Задания для самостоятельной работы
- •7.3 Вычисление пределов функции
- •8 Производная и ее приложения
- •8.1 Производная функции
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •8.2 Исследование функции при помощи производной
- •Задания для самостоятельной работы
- •9 Интеграл и его приложение
- •9.1Неопределенный интеграл
- •9.2 Методы нахождения неопределенного интеграла Метод непосредственного интегрирования
- •Замена переменной
- •Интегрирование по частям
- •9.3 Определенный интеграл
- •Методы интегрирования определенного интеграла
- •Непосредственное интегрирование.
- •3 .Интегрирование по частям
- •9.4 Приложения определенного интеграла
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Вопросы для самоконтроля
- •10 Элементы комбинаторики и теории вероятностей
- •10.1 Элементы комбинаторики
- •10.2 Основы теории вероятностей Определение вероятности.
- •Задания для самостоятельной работы
- •Список литературы
1 Линейные уравнения, системы линейных уравнений
Цель: студенты должны научиться решать системы линейных уравнений различными методами
Линейные уравнения
Линейное уравнение с одной переменой – уравнение вида ах+b=0, где а и b – некоторые постоянные. При решении линейного уравнения могут быть три случая:
1) а ≠ 0, тогда х = - в:а
2) а=0, в=0, тогда уравнение принимает вид: 0∙х=0. Корнем уравнения является любое действительное число.
3) а=0, в ≠ 0, тогда уравнение принимает вид: 0∙х=в, уравнение корней не имеет.
1.2 Системы линейных уравнений и способы их решения
Система линейных уравнений – система, все уравнения которой линейны. Прежде чем решать систему линейных уравнений, можно определить число ее решений.
1. Способ подстановки заключается в том, что в одном из уравнений выражают одну переменную через другую. Полученное выражение подставляем в другое уравнение, которое после этого обращается в уравнение с одной переменной, а затем решают его. Получившееся значение этой переменной подставляют в любое уравнение исходной системы и находят значение второй переменной.
2. Способ сложения заключается в том, что если данная система состоит из уравнений, которые при почленном сложении образуют уравнение с одной переменной, то, решив это уравнение, мы получим значение одной из переменных. Значение второй переменной находят как и в способе подстановки.
3. Графический способ заключается в том, что в одной системе координат строятся графики уравнений. Если графики пересекаются, то координаты точки пересечения являются корнями уравнений. Если графики являются параллельными прямыми, то система не имеет решений. Если графики уравнений сольются в одну прямую, то система имеет бесконечное множество решений.
1.3 Определители второго порядка
Определителем второго порядка называется число
 .
.
Задания для самостоятельной работы:
1. Вычислите определители второго порядка:
а)
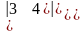 б)
б)
 в)
в)
 г)
г)
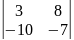
1.4 Определители третьего порядка
Определителем третьего порядка называется число
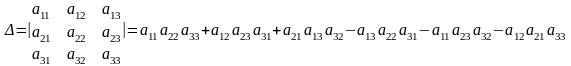 .
.
Этот способ вычисления носит название «метод треугольников Саррюса» и подчиняется следующему правилу: первые три слагаемых со знаком (+) это произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали Следующие три слагаемых со знаком (-) это произведения элементов на побочной диагонали и элементов, стоящих в вершинах треугольников, с основаниями, параллельными побочной диагонали.
Определитель можно разложить по элементам любой строки или столбца.
На практике удобно пользоваться схемами знаков алгебраических дополнений:
 -
для определителя третьего порядка;
-
для определителя третьего порядка;
При вычислении определителей удобно пользоваться следующими их свойствами:
1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонирование).
При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.
Определитель, имеющий две линейно зависимые (пропорциональные) строки (столбца) равен нулю. В частности, определитель, имеющий две одинаковые строки (столбца) равен нулю.
Общий множитель всех элементов строки или столбца можно вынести за знак определителя. В частности, определитель, имеющий нулевую строку (столбец), равен нулю.
Значение определителя не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, отличное от нуля.
Пример 1. Найти значения определителей:
а)
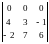 ;
б)
;
б)

Решение:
а) имеется нулевая строка; согласно свойству 4 определитель равен 0;
б) разложим определитель по элементам третьего столбца:
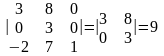 ;
;
Пример
2.
Вычислить определитель
 .
.
Решение:
Разложим определитель по элементам второй строки:
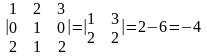 .
.
Пример 3. Вычислить определитель, разложив по элементам первой строки

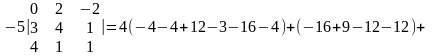
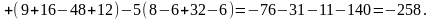
Задания для самостоятельной работы:
1.
Значение определителя равно:
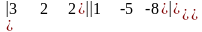
а) 11 б) 0 в) -8 г) -11
2.
Значение определителя равно:

а) 43 б) -18 в) 15 г) -16
3.Значение
определителя равно:

а) -43 б) 0 в) 58 г) 86
