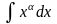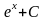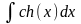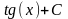- •Содержание
- •Введение
- •1 Линейные уравнения, системы линейных уравнений
- •Линейные уравнения
- •1.2 Системы линейных уравнений и способы их решения
- •1.3 Определители второго порядка
- •1.4 Определители третьего порядка
- •1.5 Решение систем трех уравнений
- •Основные тригонометрические тождества.
- •Формулы сложения аргументов
- •Тригонометрические функции удвоенного аргумента
- •Простейшие тригонометрические уравнения
- •Вопросы для самоконтроля
- •2.4 Методы решения тригонометрических уравнений
- •Разложение на множители
- •Приведение к однородному уравнению
- •Показательная и логарифмическая функции
- •Показательные уравнения и неравенства Показательные уравнения, приводимые к квадратным.
- •Задания для самостоятельной работы
- •Логарифмы и их свойства
- •3.4 Логарифмические уравнения и неравенства
- •4 Векторы
- •4.1 Декартова система координат
- •4.2Векторы на плоскости и в пространстве
- •4.3 Действия над векторами
- •Задания для самостоятельной работы
- •Вопросы для самоконтроля
- •5 Прямые и плоскости в пространстве
- •5.1 Прямые на плоскости
- •5.2 Прямые и плоскости в пространстве
- •Тема для реферата
- •6 Многогранники и тела вращения
- •6.1 Призма
- •Параллелепипед
- •Задания для самостоятельной работы
- •6.2 Пирамида
- •Задания для самостоятельной работы
- •6.3Цилиндр
- •Задания для самостоятельной работы
- •6.4 Конус Задачи для самостоятельной работы
- •6.5 Шар и сфера
- •7 Предел функции
- •7.1 Раскрытие неопределенностей вида
- •7.2 Раскрытие неопределенностей вида
- •Задания для самостоятельной работы
- •7.3 Вычисление пределов функции
- •8 Производная и ее приложения
- •8.1 Производная функции
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •8.2 Исследование функции при помощи производной
- •Задания для самостоятельной работы
- •9 Интеграл и его приложение
- •9.1Неопределенный интеграл
- •9.2 Методы нахождения неопределенного интеграла Метод непосредственного интегрирования
- •Замена переменной
- •Интегрирование по частям
- •9.3 Определенный интеграл
- •Методы интегрирования определенного интеграла
- •Непосредственное интегрирование.
- •3 .Интегрирование по частям
- •9.4 Приложения определенного интеграла
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Вопросы для самоконтроля
- •10 Элементы комбинаторики и теории вероятностей
- •10.1 Элементы комбинаторики
- •10.2 Основы теории вероятностей Определение вероятности.
- •Задания для самостоятельной работы
- •Список литературы
Задания для самостоятельной работы
Задание 1. Для указанной функции требуется провести полное исследование функции и построить её график.
1
 2.
2.
![]()
3.
![]() 4.
4.

5.
 6.
6.
![]()
7.
 8.
8.
![]()
9.
 10.
10.
![]()
11.
 .
12.
.
12.  .
.
13.
 .
14.
.
14.
 .
.
15.
 16.
16.

17.
 18.
18.

19.
 20.
20.

21.
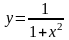 22.
22.

23.
 24.
24.

25.
 26.
26.

27.
 28.
28.

Вопросы для самоконтроля
Как применяется производная для нахождения промежутков возрастания и убывания?
Как исследуется функция на максимум и минимум с помощью второй производной?
Как определяется выпуклость кривой вверх и вниз?
Что необходимо знать для построения графика функции?
9 Интеграл и его приложение
Цель: студенты должны научиться вычислять в простейших случаях площади и объемы с использованием определенного интеграла
9.1Неопределенный интеграл
Неопределенным интегралом функции f(x) называется множество всех первообразных функций F(x) + C.
Записывается
это так:

Первообразной
функцией для функции f(x)
на промежутке (a;
b)
называется такая функция F(x),
производная которой равна f(x)
на рассматриваемом промежутке, то есть
 .
.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Ниже приводится таблица основных интегралов, которые используются при вычислениях неопределенных интегралов различных функций. Верность этой таблицы проверяется непосредственно дифференцированием.
Интеграл |
Значение |
Интеграл |
Значение |
|||
1 |
|
|
11 |
|
|
|
2 |
|
|
12 |
|
|
|
3 |
|
|
13 |
|
|
|
4 |
|
|
14 |
|
|
|
5 |
|
|
15 |
|
|
|
6 |
|
|
16 |
|
|
|
7 |
|
|
17 |
|
|
|
8 |
|
|
18 |
|
|
|
9 |
|
|
19 |
|
|
|
10 |
|
|
20 |
|
|
|
9.2 Методы нахождения неопределенного интеграла Метод непосредственного интегрирования
Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Примеры:
a)

b)
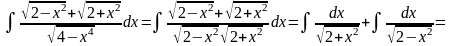

с)
 .
.