
- •Содержание
- •Введение
- •1 Линейные уравнения, системы линейных уравнений
- •Линейные уравнения
- •1.2 Системы линейных уравнений и способы их решения
- •1.3 Определители второго порядка
- •1.4 Определители третьего порядка
- •1.5 Решение систем трех уравнений
- •Основные тригонометрические тождества.
- •Формулы сложения аргументов
- •Тригонометрические функции удвоенного аргумента
- •Простейшие тригонометрические уравнения
- •Вопросы для самоконтроля
- •2.4 Методы решения тригонометрических уравнений
- •Разложение на множители
- •Приведение к однородному уравнению
- •Показательная и логарифмическая функции
- •Показательные уравнения и неравенства Показательные уравнения, приводимые к квадратным.
- •Задания для самостоятельной работы
- •Логарифмы и их свойства
- •3.4 Логарифмические уравнения и неравенства
- •4 Векторы
- •4.1 Декартова система координат
- •4.2Векторы на плоскости и в пространстве
- •4.3 Действия над векторами
- •Задания для самостоятельной работы
- •Вопросы для самоконтроля
- •5 Прямые и плоскости в пространстве
- •5.1 Прямые на плоскости
- •5.2 Прямые и плоскости в пространстве
- •Тема для реферата
- •6 Многогранники и тела вращения
- •6.1 Призма
- •Параллелепипед
- •Задания для самостоятельной работы
- •6.2 Пирамида
- •Задания для самостоятельной работы
- •6.3Цилиндр
- •Задания для самостоятельной работы
- •6.4 Конус Задачи для самостоятельной работы
- •6.5 Шар и сфера
- •7 Предел функции
- •7.1 Раскрытие неопределенностей вида
- •7.2 Раскрытие неопределенностей вида
- •Задания для самостоятельной работы
- •7.3 Вычисление пределов функции
- •8 Производная и ее приложения
- •8.1 Производная функции
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •8.2 Исследование функции при помощи производной
- •Задания для самостоятельной работы
- •9 Интеграл и его приложение
- •9.1Неопределенный интеграл
- •9.2 Методы нахождения неопределенного интеграла Метод непосредственного интегрирования
- •Замена переменной
- •Интегрирование по частям
- •9.3 Определенный интеграл
- •Методы интегрирования определенного интеграла
- •Непосредственное интегрирование.
- •3 .Интегрирование по частям
- •9.4 Приложения определенного интеграла
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •Вопросы для самоконтроля
- •10 Элементы комбинаторики и теории вероятностей
- •10.1 Элементы комбинаторики
- •10.2 Основы теории вероятностей Определение вероятности.
- •Задания для самостоятельной работы
- •Список литературы
Задания для самостоятельной работы
а)
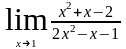 б)
б)
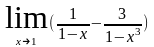
а)
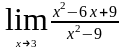 б)
б)
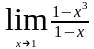
а)
 б)
б)
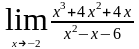
а)
 б)
б)
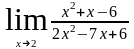
а)
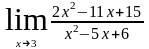 б)
б)
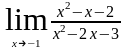
а)
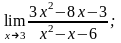 б)
б)
а) б)
а) б)

а)
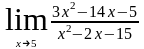 б)
б)
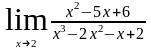
а)
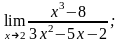 б)
б)

7.3 Вычисление пределов функции
Пример. Найти пределы функции.
1.

2.

Решение:
Выяснив вначале, что при указанном изменении аргумента данная функция представляет отношение двух бесконечно малых величин (случай
 ),
преобразуем затем дробь так, чтобы
сократить ее на множитель, стремящийся
к нулю: переведем иррациональность из
числителя в знаменатель путем умножения
числителя и знаменателя на
),
преобразуем затем дробь так, чтобы
сократить ее на множитель, стремящийся
к нулю: переведем иррациональность из
числителя в знаменатель путем умножения
числителя и знаменателя на
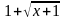 ,
затем сократим дробь на х:
,
затем сократим дробь на х:
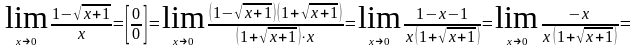
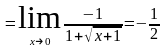 .
.
2. . Для раскрытия неопределенности вида избавимся от иррациональности, умножив числитель и знаменатель на выражение, сопряженное числителю. Получим:
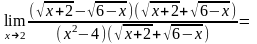
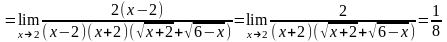 .
.
Задания для самостоятельной работы
а)
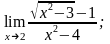 б)
б)

а)
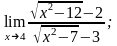 б)
б) 
а)
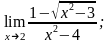 б)
б)
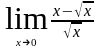
а)
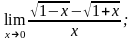 б)
б)
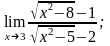
а)
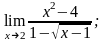 б)
б)
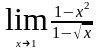
а)
 б)
б)

а)
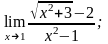 б)
б)
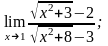
а) б)

а)
 б)
б)
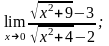
а)
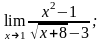 б)
б)
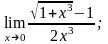
а)
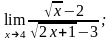 б)
б)
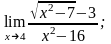
а) б)

а)
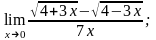 б)
б)
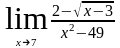
а)
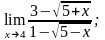 б)
б)
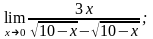
а)
 б)
б)
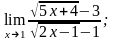
а)
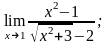 б)
б)
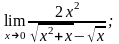
8 Производная и ее приложения
Цель: студенты должны уметь находить производные элементарных функций; использовать производную для изучения свойств функций и построения графиков
8.1 Производная функции
Первое правило.
Производная суммы равна сумме производных:
(u+v)’= u’+v’
Второе правило.
Умножение:
(u*v)’=u'*v +u*v'
Третье правило.
Деление.

Следствие.
Постоянный множитель можно вынести за знак производной.
(c*u)’=c*u’
примеры:
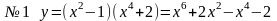

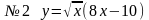
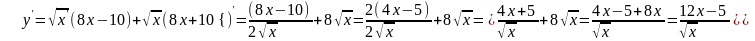
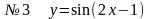
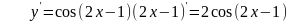



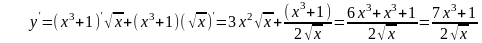
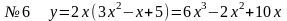
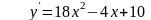
№7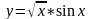

№8
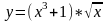

№9
у =
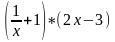
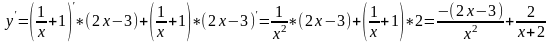
№10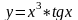
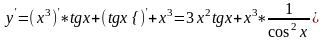
№11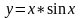

№12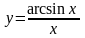
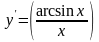 =
=
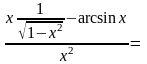
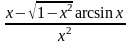
№13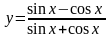
 =
=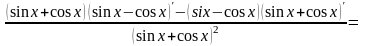


№14 y(x) = tg x
![]()
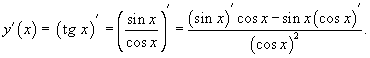
![]()
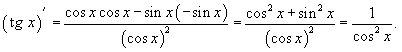
№15 f(x) = x2 + sin x;
f ’(x) = (x2 + sin x)’ = (x2)’ + (sin x)’ = 2x + cos x;
Производная сложной функции.
Пусть даны две функции: 1) у=sinx - простая
у=sin (x2+1) – сложная
В первой функции аргумент х, во второй аргумент (х2+1), то есть одна функция зависит от другой функции.
Функция,
заданная формулой
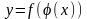 ,
называется сложной функцией, составленной
из двух функций f
и
,
называется сложной функцией, составленной
из двух функций f
и
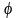 .
.
Например:
1.
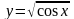
2.
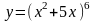
Производная сложной функции вычисляется по формуле:
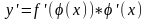
Примеры:
1. Найти производную функции:

Решение:

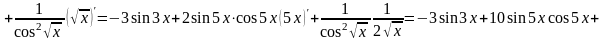
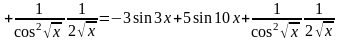
2.
![]() ;
;
Решение.
![]() ,
где
,
где
![]()
![]() =
=![]() ;
;
![]()
![]()
![]()
![]()
3.

Решение.


 .
.
