7. Синусоидальный ток. Получение.

Цепью переменного тока называется цепь ток i(t) и напряжение u(t) которой, периодически изме­няются во времени по направлению. Из-за экономичности работы приёмников и простоты получения более широко используются цепи, параметры которых, изменяются по гармоническому синусоидальному закону.

Синусоидальную эдс можно получить с помощью однофазного генератора. В витке обмотки вращающейся в однофазном магнитном поле , где - активная сторона длины витка, - линейная скорость перемещения витка относительно магнитного поля

1) амплитудное значение (максимальное)

2) период Т – промежуток времени в течении которого эдс совершает полный цикл изменения

3)частота f количество полных циклов изменения за 1 сек.

4)фаза аргумент синусоидальной функции

5)начальная фаза значение фазы в момент времени t=0

Введем, аналогично эдс, значение тока и напряжения

i(t)=I_m sin(t+_i),

u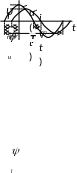 (t)=U_msin(t+_u)

6) сдвиг фаз – разность начальных фаз

Значения параметров (токов, напряжений, эдс) в любой момент времени называют моментальными значениями этих величин. При расчёте режимов работы цепей, для упрощения расчётов, используют действующие (эффективные) значения этих параметров. Под действительным значением понимают его значение 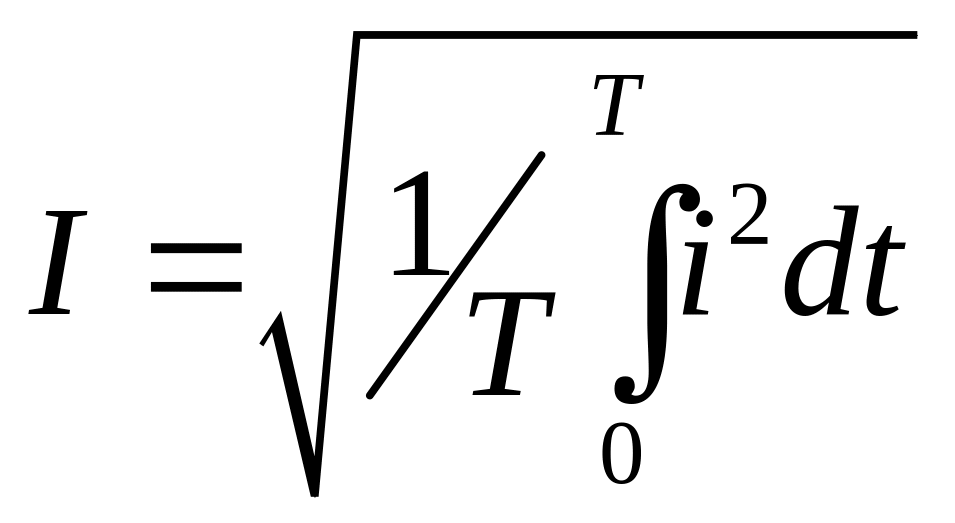подставив i(t)=I_m sin(t+_i) ) получим аналогично для других параметров режима, где - максимальное значение параметра.

В цепях, где ток изменяется по периодическому несинусоидальному закону

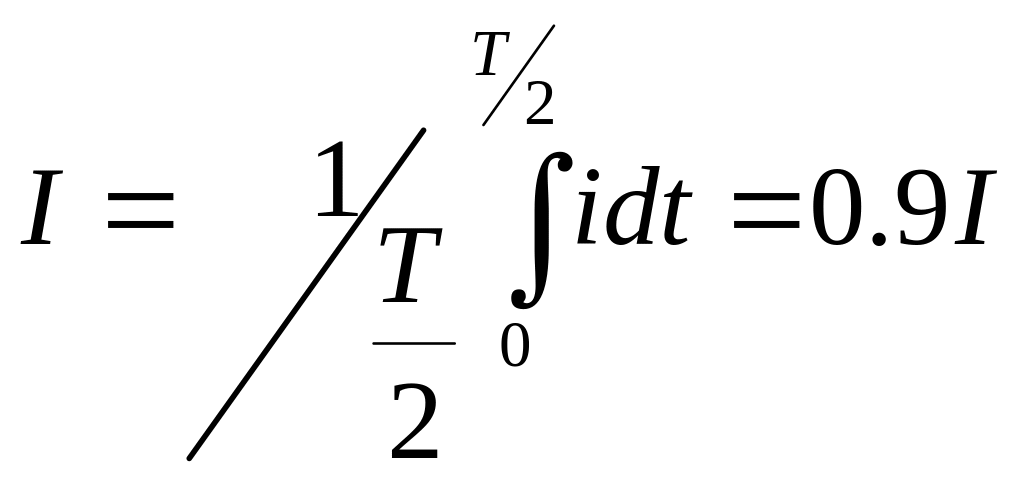
8. Представление синусоидальных величин вращающимися векторами на декартовой и комплексной плоскости.

При расчётах используют следующие способы представления электрических величин.

1)табличный в форме зависимости режима от времени. Неудобен в расчетах.

2)в форме изображающих векторов в декартовой системе координат. Проекция изображающего вектора на ось ординат даёт его мгновенное значение. Совокупность векторов называют векторной диаграммой ВД этой цепи, так как все векторы вращаются с одинаковой скоростью, то взаимное расположение векторов не изменяется, и вектора располагаются под углами равными начальным фазам. Расчет осуществляется с помощью геометрических операций над изображающими векторами. Но этот метод громоздок и существует неоднозначность в расчетах.

3) поэтому используют способ представления в виде изображающих векторов на комплексной плоскости. Его получают заменой оси абсцисс осью действительных значений, а ось ординат – осью мнимых величин. Таким образом, геометрические операции над изображающими векторами заменяются на операции над комплексными числами, соответствующие концам этих изображающих векторов.

Наиболее рациональным способом представления переменных электрических величин является их представление в виде изображающих векторов на комплексной плоскости, ориентированных по отношению к оси действительных величин под углами равными их начальным фазам. Данный метод расчета называют комплексным.

9 Последовательное соединение R, L, С элементов. Полное сопротивление, закон Ома, векторная диаграмма напряжений. Резонанс напряжений.

По 2-му закону Кирхгофа для цепи получим что:

_{Учитывая что 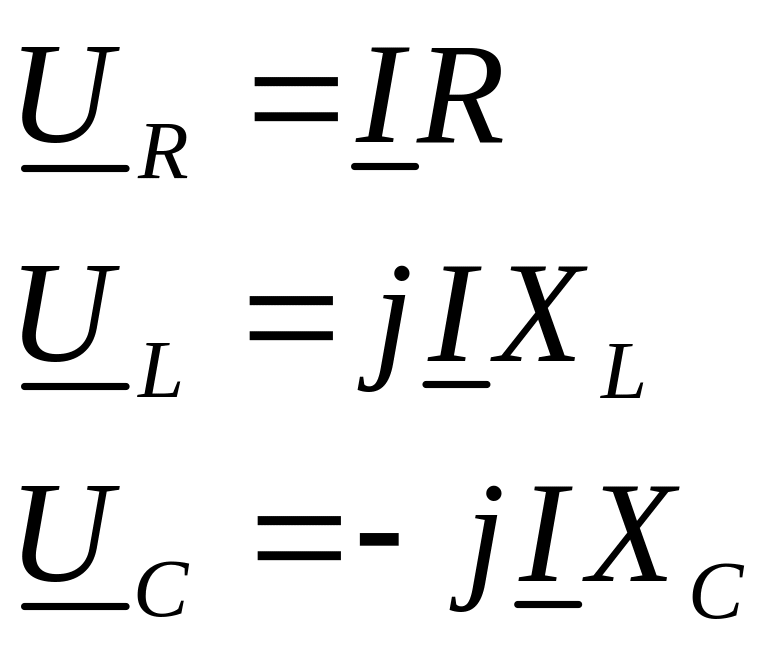Получим что}

где  комплексное полное сопротивление цепи

, где

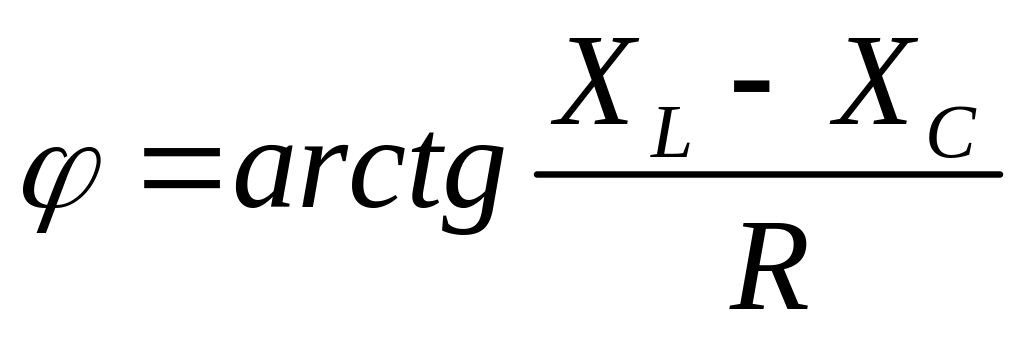
а )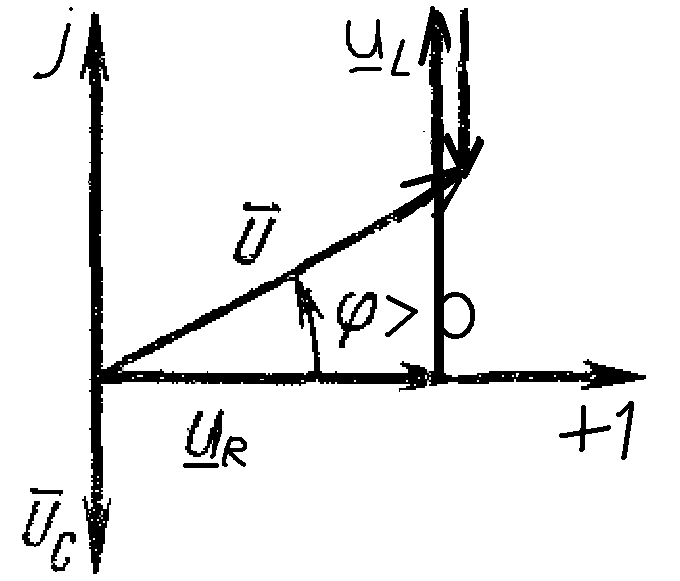

Из ВД видно что ф>0, т.е. цепь в искомом ведет себя по отношению к источнику как активно индуктивный приемник т.е. потребляет активную мощность реактивную мощность

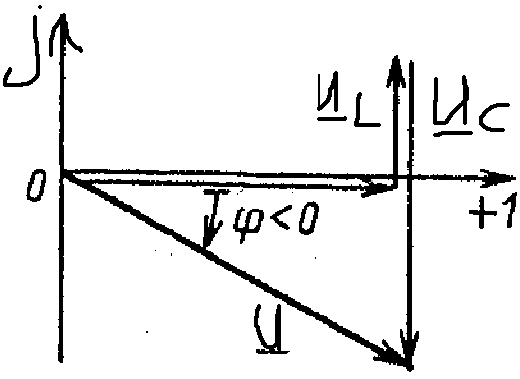
б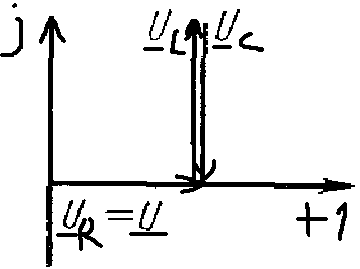 ) т.е. цепь имеет в целом активно емкостной характер т.е. ток I опережает U на угол ф , на входе цепи. Цепь потребляет от источника активную мощность и отдает источнику генерирует реактивную мощность

с) В этом случае в цепи имеет место резонанс напряжений условием которого является

Следствие резонанса напряжений

1. Ф=0, т.е. совпадение по фазе U и I

2.

3.

4. В контуре близком к идеальному (т.е. с малым сопротивлением R) возможно появление перенапряжений на реактивных элементах контура, т.к. , , где