
- •Кафедра «Теория механизмов и машин» теория механизмов и машин конспект лекций
- •Лекция 31. Пространственные зубчатые передачи.
- •1.2. Механизмы современной техники.
- •1.3. Задачи и основные методы теории механизмов и машин.
- •План лекции
- •1. 5. 2 Классификация кинематических пар по числу связей.
- •1.5.3 Степень подвижности кинематической цепи.
- •5. 7 Избыточные связи.
- •План лекции
- •1. 5. 5 Образование механизма из кинематической цепи.
- •1. 5. 6 Принцип образования механизмов по Ассуру.
- •1. 5. 6 Принцип образования механизмов по Ассуру.
- •1. 5. 7 Избыточные связи
- •1. 5. 8 Классификация механизмов по общим свойствам.
- •1.5.9 Виды механизмов.
- •Тема 2
- •Лекция 4 План лекции
- •2. 2 Графический метод кинематического анализа - метод кинематических диаграмм.
- •2. 2. 1 Определение положений звеньев, построение траекторий точек и кинематических диаграмм.
- •2. 2. 2 Графическое дифференцирование.
- •2.2.3 Графическое интегрирование.
- •2.3.1 Построение планов скоростей.
- •2.3.2 Построение планов ускорений.
- •2.5 Метод преобразования координат.
- •2.5.1. Определение положений точек в незамкнутых кинематических цепях.
- •2.5.2 Определение положений точек в замкнутых кинематических цепях.
- •2. 14 Преобразование координатных систем.
- •2 .5.4 Уравнения преобразования координат для конкретных кинематических пар,
- •5. 5 Определение положения захвата пространственного манипулятора в неподвижной системе координат.
- •Лекция 8
- •2.5.6 Определение положения точек в плоских механизмах
- •2.5.7 Определение положений точек, скоростей и ускорений
- •2.5.6 Определение положений точек в плоских механизмах векторным методом.
- •2.5.7 Определение угловых скоростей и ускорений звеньев и линейных скоростей и ускорений точек плоских механизмов. Аналоги скоростей и ускорений.
- •3.1. Введение в динамику машин.
- •3.2.1 Классификация сил.
- •3.1 Введение в динамику машин.
- •3.2. Силы, действующие в машинах.
- •3.2.1 Классификация сил.
- •Внешние и внутренние силы.
- •2. Силы движущие и силы сопротивления.
- •3.2.2 Определение сил инерции.
- •3.4.Кинетостатический расчет механизмов.
- •3.4.1 Задачи кинетостатики механизмов.
- •3.4.2 Условия статической определимости групп звеньев.
- •3.4.3 Графоаналитический метод кинетостатического расчета групп второго класса.
- •2. Группа 2-го вида
- •3.4.4 Аналитический метод кинетостатического
- •3.4.5 Кинетостатика ведущего звена.
- •3.4.4 Аналитический метод кинетостатического
- •Лекция 12. План лекции.
- •3.5.1 Трение в поступательных кинематических
- •3.5.2 Трение во вращательной кинематической паре.
- •3. 6. Передача работы и мощности. Кпд машин. Коэффициент потерь.
- •3.6.1 Кпд поступательной кинематической пары.
- •3.6.3. Определение кпд механизма.
- •3.6.4 Кпд соединенных машин.
- •3.7.1 Общие условия уравновешивание вращающихся масс.
- •3.7.2 Статическое уравновешивание.
- •Уравновешивание в общем случае или динамическое уравновешивание.
- •3.7.4 Статическая и динамическая балансировка вращающихся масс.
- •3.7.6. Уравновешивание шарнирного четырехзвенника.
- •3.8. Движение машин под действием заданных сил.
- •3.8.1. Режимы движения машины.
- •3.8.2. Характеристика внешних сил.
- •Кинетическая энергия звеньев и работа сил, действующих в машинах.
- •Приведение сил и масс .Динамические модели машины.
- •Определение приведенных моментов инерции и моментов сил кривошипно-ползунного механизма.
- •Приведение сил и масс. Динамические модели машины.
- •3.8.5 Определение приведенных моментов инерции и моментов сил кривошипно – ползунного механизма.
- •Лекция 16.
- •3.8.7. Уравнения движения машины в форме интеграла энергии.
- •3.8.8 Уравнения движения в дифференциальной форме.
- •Разрешим уравнение (3.57) относительно углового ускорения
- •3.8.13 Определение момента инерции маховика.
- •3.8.16 Уравнения движения машины с учетом упругости звеньев.
- •Тема 4. Общие методы синтеза механизмов. (4 часа).
- •План лекции
- •4. 1. Основные задачи и метода синтеза.
- •4. 2. Основные и дополнительные условия синтеза. Ограничения при синтезе.
- •4. 3. Методы оптимального синтеза.
- •4. 4. Синтез механизмов на основании заданной целевой функции.
- •4. 5. Интерполяционный метод синтеза механизмов.
- •Лекция 20.
- •4.6. Синтез механизмов методом наилучшего приближения функций.
- •4.7. Метод квадратичного приближения.
- •4.6. Синтез механизмов методом наилучшего приближения функций.
- •4.7. Метод квадратичного приближения.
- •Тема 5 Синтез плоских рычажных механизмов (4 часа) Лекция 21 План лекции
- •5.1 Основные условия и ограничения при синтезе.
- •5.2 Синтез четырехзвенного кривошипно-коромыслового. Механизма по трем положениям, аналитическим методом.
- •5.3 Синтез четырехзвенного кривошипно-коромыслового механизма по двум крайним положениям коромысла, коэффициенту изменения средней скорости и допускаемому углу давления.
- •5.1 Основные условия и ограничения при синтезе.
- •5.2 Синтез четырехзвенного кривошипно-ползунного коромыслового механизма по трем положениям аналитическим методом.
- •5.3 Синтез четырехзвенного кривошипно-коромыслового механизма по двум крайним положениям коромысла, коэффициенту изменения средней скорости и допускаемому углу давления.
- •План лекции
- •5.4.L Синтез кривошипно-коромыслового механизма.
- •5.4.2 Синтез кривошипно-ползунного механизма.
- •5.4.З Синтез кулисного механизма.
- •9.2. Фазы движения толкателя
- •9.3. Обоснование выбора закона движения
- •Лекция 24. План лекции.
- •6.4. Кинематический анализ кулачковых механизмов.
- •6.5 Синтез кулачковых механизмов.
- •6.6 Проектирование по кинематическим параметрам. Построение профиля кулачка при поступательном движении толкателя.
- •6.4 Проектирование по динамическим параметрам. Определение текущих углов давления. Аналог скорости
- •Лекция 25 План лекции.
- •6.10. Графическое определение текущих углов давления.
- •6.11 Аналитический метод определения основных размеров кулачкового механизма по заданному допускаемое углу давления.
- •6.12. Силовой расчет кулачкового механизма.
- •Глава 7. Синтез зубчатых зацеплений. (12 часов).
- •7.2. Основная теорема зацепления. Полюс зацепления. Центроиды колес.
- •7.3. Цилиндрическая эвольвентная зубчатая передача..
- •7.1 Виды зубчатых механизмов
- •7.2. Основная теорема зацепления. Полюс зацепления. Центроиды колес.
- •7.3. Цилиндрическая эвольвентная зубчатая передача.
- •Окружность
- •Окружность
- •5. Эвольвента - кривая без перегибо Лекция 27. План лекции
- •7.4. Элементы эвольвентного зубчатого колеса
- •Элементы и свойства эвольвентного зацепления
- •7.6 Коэффициент перекрытия
- •7.4. Элементы эвольвентного зубчатого колеса
- •7.5 Элементы и свойства эвольвентного зацепления
- •7.6. Коэффициент перекрытия
- •Лекция 28. План лекции
- •7.7. Интерференция зубьев. Условие отсутствия заклинивания
- •7.8. Внутреннее зацепление (рис.7.9)
- •7.9. Реечное зацепление (рис.7.10)
- •7.10. Изготовление зубчатых колес.
- •Лекция 29. План лекции
- •Смещение исходного контура и его влияние на форму нарезаемых зубьев.
- •Определение размеров колеса
- •7.14. Толщина зуба по произвольной окружности.Условие отсутствия заострения
- •7.15. Условие отсутствия подрезания
- •7.16 Эвольвентное беззазорное зацепление. Определение межосевого расстояния и угла зацепления. Воспринимаемое и уравнительное смещение.
- •7.17 Проектирование зубчатых передач. Выбор коэффициента смещения.
- •7.18 Косозубая цилиндрическая передача,
- •7.17 Проектирование зубчатых передач. Выбор коэффициента смещения.
- •7.18 Косозубая цилиндрическая передача.
- •7.21 Передачи с перекрещивающимися осями.
- •7.21.1 Винтовая передача.
- •7.21.2 Червячная передача.
- •Тема 8. Синтез механизмов с подвижными осями. Лекция 32.
- •Кинематическое исследование планетарных механизмов графическим методом Куцбаха – Смирнова.
- •Тема 9. Основы теории машин - автоматов. ( 4 часа)
- •План лекции:
- •9.1.2. Управление от копиров.
- •9.1.3. Следящий привод.
- •Промышленные роботы
- •9.3. Рабочий объем манипулятора и классификация движений захвата
- •9.4. Влияние расположения кинематических пар манипулятора на его маневренность
- •9.5 Структурный синтез манипуляторов
- •9.6 Зоны обслуживания, угол и коэффициент
- •Список литературы.
Тема 8. Синтез механизмов с подвижными осями. Лекция 32.
План лекции
8.1 Планетарные и дифференциальные механизмы.
Кинематический анализ планетарных механизмов. Метод Виллиса.
Кинематическое исследование планетарных механизмов графическим методом Куцбаха – Смирнова.
Дополнительные условия синтеза планетарного механизма.
Подборчисел зубьев планетарного механизма.
8.1 Планетарные и дифференциальные механизмы.
Планетарным называется сложный зубчато-рычажной механизм, в котором оси некоторых колес перемещаются в пространстве.
Основные определения.
На рис.8.1,а представлен простейший планетарный механизм. Колеса с неподвижными осями (1-е и 3-е) называются солнечными или центральными. Неподвижное центральное колесо называется опорным (3). Колеса с подвижными осями называются сателлитами (2). Звено, на котором расположены оси сателлитов, называются водило (Н).
Сателлит участвует в двух вращательных движениях: переносном и относительном. Обычно имеется несколько симметрично расположенных сателлитов: к=2…8. Такая многопоточная передача энергии одновременно несколькими зубчатыми парами позволяет уменьшить габариты и массу планетарных передач по сравнению с обычными зубчатыми передачами. Правда, такой механизм имеет избыточные связи, и требуется высокая точность изготовления передачи, чтобы сателлиты были нагружены равномерно.
Структура механизмов.
В механизме (см. рис. 8.1,а) имеет: n = 3(1,2. Н), pn= 3(1/ 3, 2/ Н, Н/a ), pв = 2(1/ 2, 2/ 3). Тогда число степеней свободы
W = 3n – 2pн –рв = 33 – 23 – 2=1.
Если освободить опорное колесо 3 (рис.8.1.б) и сообщить ему движение, то все колеса станут подвижными: n= 4, pn= 4, pв =2.
W = 3 4 – 2 4 –2 = 2
Механизмы, у которых число степеней свободы W2, называются дифференциалами .
Число степеней свободы дифференциального механизма показывает, скольким звеньям необходимо сообщить независимые движения, чтобы получить определенность движения остальных звеньев. В зависимости от направления вращения колес может происходить либо разложение движения, либо сложнее. Обычно W5.
Любой планетарный механизм можно превратить в дифференциальный, если освободить опорное колесо и сообщить ему движение. Наоборот, любой дифференциал можно превратить в планетарный механизм, если закрепить одно (при W =2) или несколько из его центральных колес (свойство обратимости планетарного механизма).
Достоинства и недостатки.
Преимущества механизмов:
Возможность получения большого передаточного отношения при малом числе колес (от 3 – 8 до десятков тысяч).
Большой диапазон регулирования скорости ведомого звена при небольшом диапазоне изменения скорости ведущего звена.
Дифференциалы позволяют суммировать мощность при одном потребителе или раскладывать ее на несколько потребителей.
Возможность передачи больших мощностей при малых размерах редукторов.
Высокий КПД (до 0,98).
Легкая изменяемость схемы (с помощью тормозов).
Недостаток: повышенная сложность расчета, изготовления и сборки (в особенности при К > 3).
Планетарные механизмы нашли широкое применение в промышленности. Они используются в качестве редукторов и мультипликаторов, суммирующих механизмов, реверсивных, коробок скоростей и других механизмов приводов.
8.2 Кинематический анализ планетарных механизмов.Метод Виллиса.
Существует три метода кинематического анализа:
Аналитический метод Виллиса
Графический метод Кутцбаха – Смирнова
Табличный метод Свампа
При кинематическом исследовании существующих или новых механизмов определяют передаточные отношения, линейные и угловые скорости.
Метод Виллиса.
Метод основан на обращении движения. Пусть звенья механизма движутся со скоростями 1, 2, н, 3 .Всем звеньям сообщается угловая скорость, равная по величине, но противоположная по направлению угловой скорости водила н. Водило остановится, и механизм превратится в зубчатый механизм с неподвижными осями, состоящий из нескольких последовательно соединенных колес (обращенный механизм). Но скорости колес будут иными:
1н=1-н, 2н=2-н, 3н=3-н, нн=0;
Передаточное отношение от 1-го колеса к 3-ему в обращенном движении:
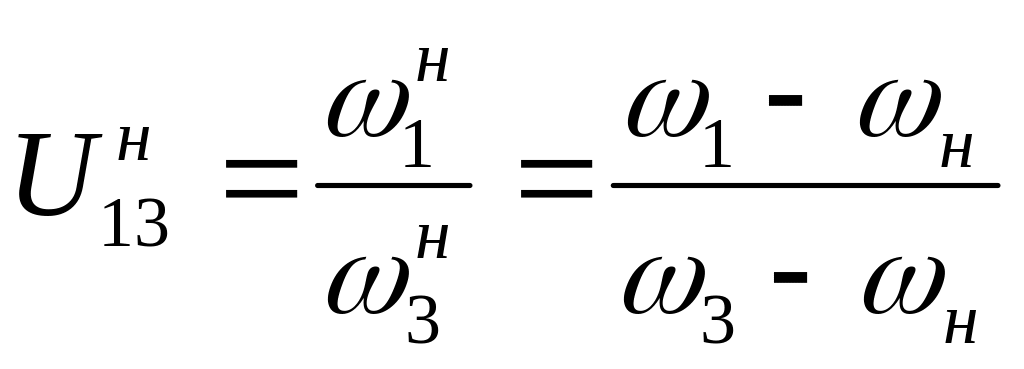 (8.1)
(8.1)
В общем виде:
![]()
Для дифференциального механизма формула Виллиса записывается в виде:
-1+U13н3+(1-U13н)н=0. (8.2)
Это уравнение связывает угловые скорости колес 1 и 3 водила Н. Задаваясь двумя из них, можно определить третью.
В планетарном механизме 3= 0, тогда из (8.1) получим:
![]() ,
,
где U1н3=1н – передаточное отношение реального механизма.
Формула Виллиса для планетарного механизма имеет вид:
Uпл=U1н3=1-U13н.
