7.18 Косозубая цилиндрическая передача.

Для улучшения плавности передачи, связанной с увеличением коэффициента перекрытия, или уменьшения числа зубьев колес, изготовляетлых методом огибания стандартным инструментом, применяют косозубые колеса.

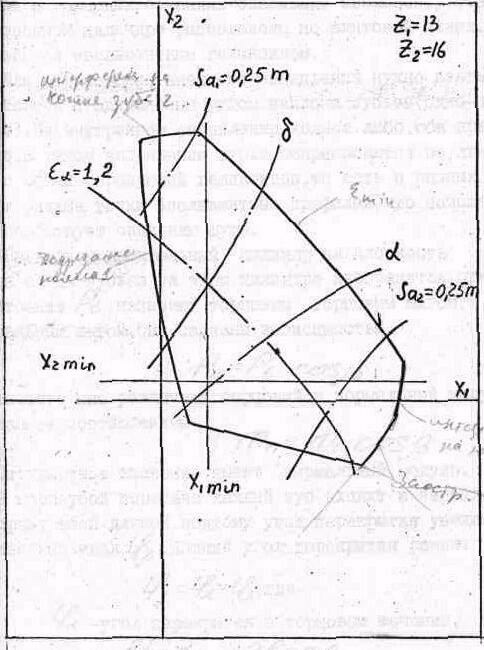
Рис. 7.17 Блокирующий контур

Боковую поверхность косого зуба эвольвентного колеса можно представить как линейчатую поверхность, описываемую прямой, лежащей в плоскости Q под углом к образующей основного цилиндра, по которому эта плоскость катится без скольжения - угол наклона зубьев на основном цилиндре. Каждая точка прямой в торцовых сечениях описывает эвольвенту. Основания эвольвент на основном цилиндре расположены по винтовой линии. Вся поверхность называется эвольвентным геликоидом.

Для образования внешнего зацепления нужно взять два косозубых колеса с одинаковым утлом наклона зубьев (одно - правое, другое - левое). Во внутреннем зацеплении колёса либо оба правые, либо оба левые. В таком зацеплении зубья соприкасаются по линии, совпадающей с общей образующей геликоидов, то есть в разных сечениях участвуют разные точки эвольвентных профилей, что повышает плавность и способствует снижению шума.

Развернем делительный цилиндр на плоскость

Тогда следы зубьев на этом цилиндре изобразятся прямыми линиями. Расстояние P_t называют торцовым шагом, а расстояние P_n нормальным шагом. Они связаны зависимостью.

Соответственно различают торцовый и нормальный модули m_t, m_n, cвязанные соотношением

Стандартное значение имеет нормальный модуль.

В косозубой передаче каждый зуб входит в зацепление постепенно, не сразу всей длиной, поэтому угол перекрытия увеличивается на ддобавочный угол . Полный угол перекрытия равен:

, где

- угол перекрытия в торцовом сечении,

b -ширина колеса,

- радиус делительного цилиндра.

Соответственно увеличивается и коэффициент перекрытия.

Он определяется выражением

Здесь коэффициент перекрытия в торцовом сечении,

Одним из недостатков косозубых передач является наличие осевого усилия, что усложняет конструкцию опор. Этот недостаток устраняется применением шевронных колес.

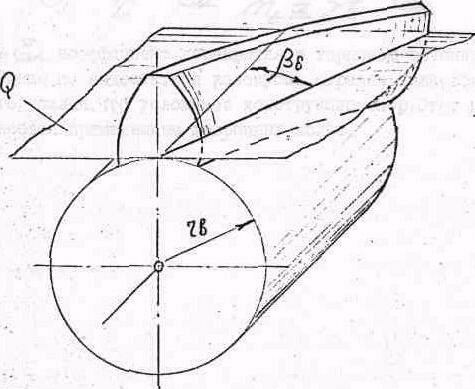
Рис. 7.18 Образование эвольвентного геликоида

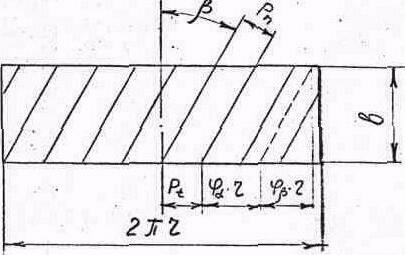
Рис. 7.19 Развертка делительного цилиндра

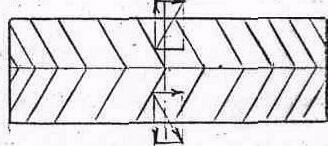
Рис. 7.20 Шевронное колесо

Лекция 31

План лекции

7.19 Пространственные зубчатые передачи.

7.20 Коническая передача.

7.21 Передачи с перекрещивающимися осями.

7.21.1 Винтовая передача.

7.23.2 Червячная передача.

7.19 Пространственные зубчатые передачи.

Пространственные зубчатые передачи классифицируют: на передачи с параллельными осями или цилинрические,передачи с пересекающимися осями или конические и передачи с перекрещивающимися осями или гиперболоидные.

Конической передачей называется передача с пересекающимися осями вращения. Пусть имеются два звена вращающиеся с угловыми скоростями w₁ и w₂. Из механики известно, что относительное движение этих звеньев, в данном случае можно свести к вращению вокруг мгновенной оси вращения ОР. Положение этой оси совпадает с вектором относительно угловой скорости звеньев.

w₂₁=w₂+(-w₁)

На оси ОР линейные скорости соприкасающихся точек звеньев равны между собой ,т.е. в точке Р.

V_P1=V_P2, r_W1=l_OPsin₁; r_W2=l_OPsin₂

откуда

w₁r_W1=w₂r_W2; w₁l_OPsin₁=w₂l_OPsin₂; U₁₂=sin₂/sin₁

где, ₁ ₂ – углы начальных конусов;

r_W1 и r_W2 – радиусы по вершинам начальных конусов.

Последовательные положения оси ОР в системах звеньев образуют аксоиды (геометрические места мгновенных осей вращения) в виде конических поверхностей называемых начальными конусами.

Начальные конусы имеют общую вершину в (.) О и перекатываются один по другому без скольжения.

Если на боковой поверхности начальных конусов нанести зубья, то получим коническую передачу с пересекающимися осями.

Рассмотрим образование боковой поверхности зуба конического колеса.

При качении по основное конусу некой плоскости q прямая 00, лежащая на ней и проходящая через вершину конуса, опишет боковую эвольвентную поверхность зуба, а каждая точка этой прямой кривую, называемую сферической эвольвентой.

Высоту зуба ограничивает конус вершин. Размеры зуба к вершине а уменьшаются.

Элементы конического колеса.

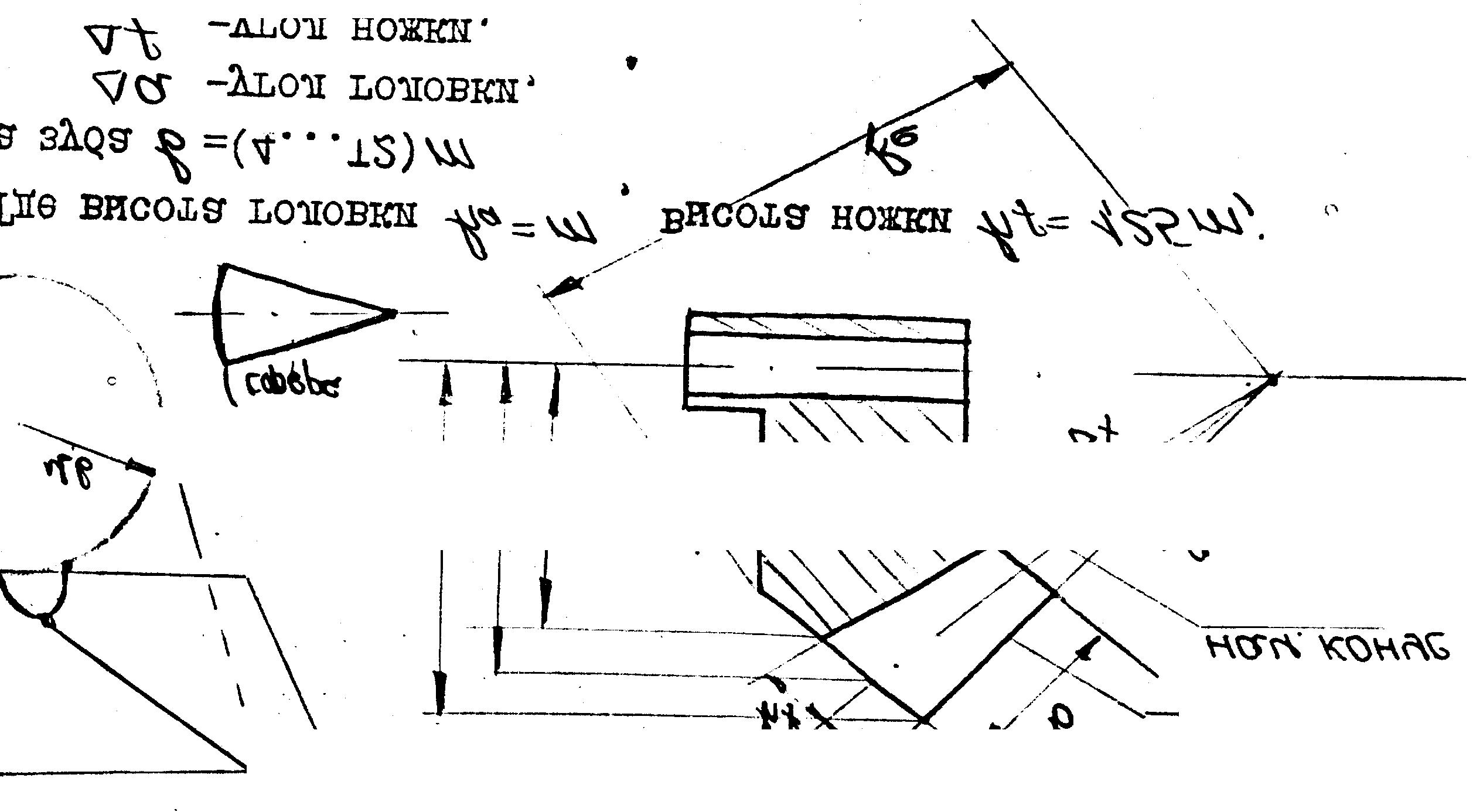
R_e – конусное расстояние;

r_a -радиус конуса головки;

r_f – радиус конуса ножки.

Для оценки конической передачи по условиям ограничения (коэффициент перекрытия _, отсутствие интерференции и т. д.) и для оценки изгибной прочности применяют искусственный прием - способ Третгольда.

Сферическую торцовую поверхность колеса заменяют на коническую, образующие которой перпендикулярны начальным конусам. В пределах высоты зуба конус и сфера отличаются незначительно. Этот конус называется дополнительным.

Если дополнительные конусы двух колес, находящихся в зацеплении, развернуть на плоскость, то по этим разверткам можно построить эквивалентное цилиндрическое зацепление рис.

Число зубьев в таком зацеплении

Z_экв=Z/cos;

По характеристикам колес в эквивалентном зацеплении можно судить об условиях ограничения и вести расчеты на прочность.